原命題
我們從下面的題目直接看一般情況:
eg: 判定級數 \(a_n = \displaystyle\frac{1}{n^p}(n \geq 1, p > 0)\) 的斂散性.
解:\(f(x) = x^{-p}\) 在 \([1, +\infty)\) 上單調減;積分 \(\int_1^{+\infty} x^{-p}dx\) 在 \(p > 1\) 時收斂,在 \(p \leq 1\) 時發散. 由定理4(積分判別法),級數 \(\sum{n^{-p}}\) 在 \(p > 1\) 時收斂,在 \(p \leq 1\) 時發散。
擴展
eg: 判斷 \(a_n = \displaystyle\frac{1}{n}\) 的斂散性.
解:直接可以看出 \(\displaystyle\frac{1}{n}\) 單調減且收斂於零,故由定理 6(萊布尼茨判別法) 知級數 \(\sum{(-1)^{n - 1}a_n}\) 收斂.
附
1、定理4(積分判別法) 設 \(f(x)\) 在區間 \([1, +\infty)\) 上非負且單調減,\(a_n = f(n)\ (n = 1,2,...)\),則級數 \(\sum{a_n}\) 收斂當且僅反常積分 \(\int_1^{+\infty}f(x)dx\) 收斂.
證明:

2、反常積分的定義:

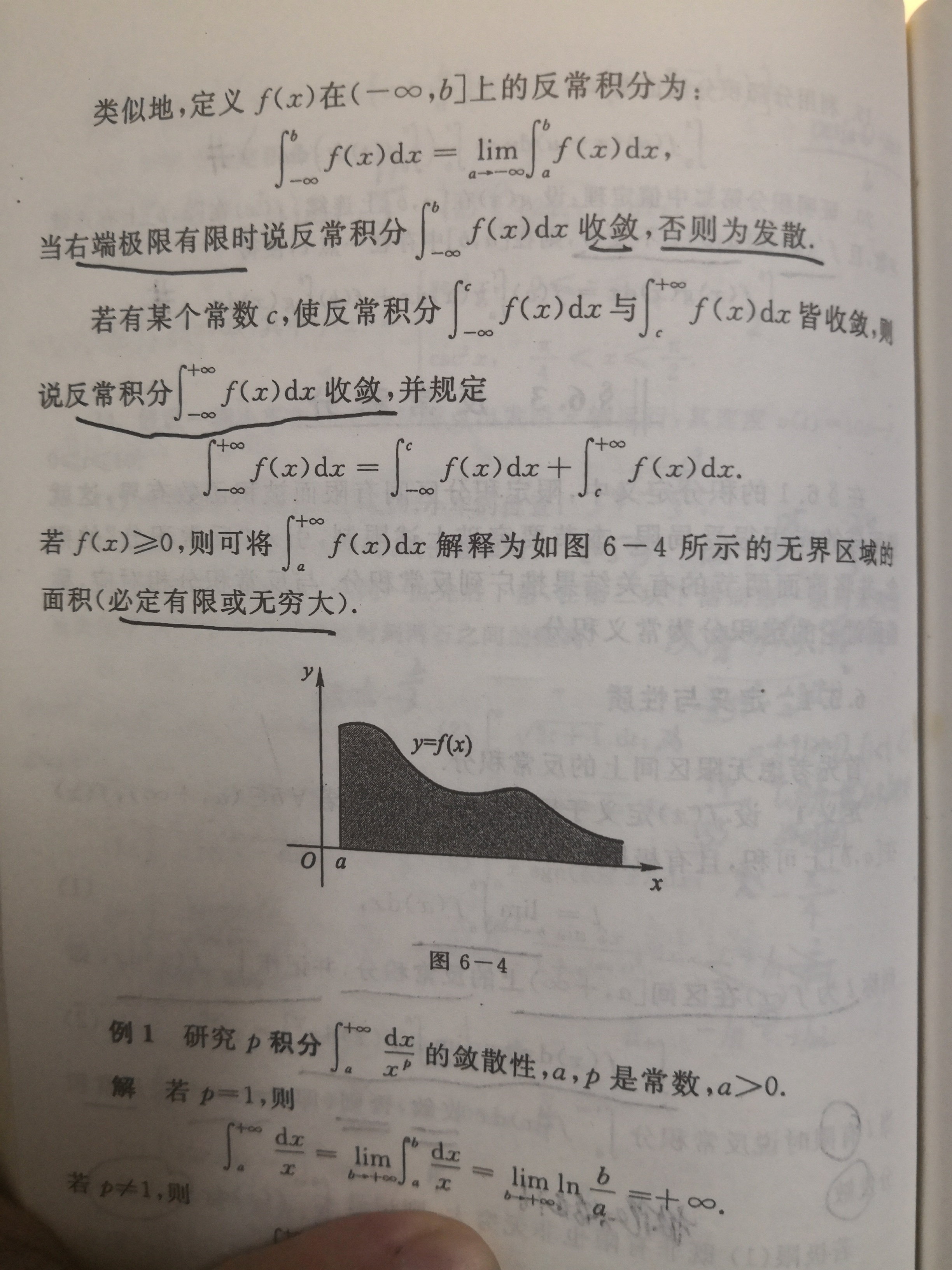
3、定理 6:Leibniz 判別法

參考:華科微積分教材
