卡諾定理的證明

1、定義

2、證明

2.1、課堂上講的證明

2.2、網絡版證明

由於我對這個證明的理解有點模糊，所以又在網上重新找了一個證明，就是下面這個，結合一下就清晰了許多。

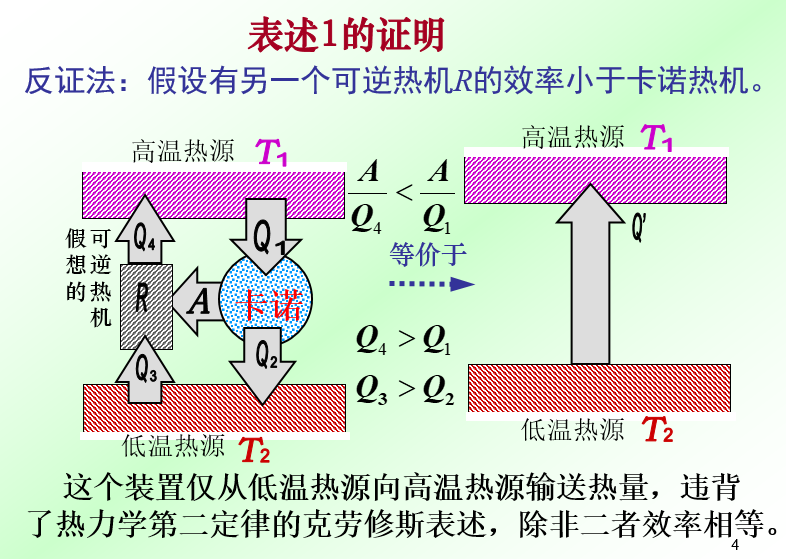
(1) 證明卡諾定理1：
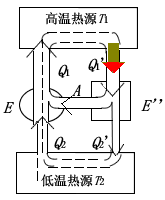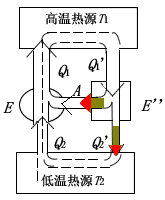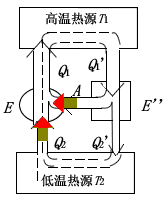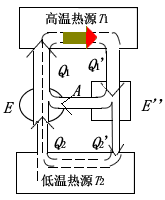
設有可逆機 \(E\) 和 \(E'\)，令 \(E'\) 作正循環，\(E\) 作逆循環，將它們組成復合機，如圖所示，可以調節它們滿足

\[A = Q_1^{'} - Q_2^{'} = Q_1 - Q_2 \qquad \qquad ① \]

用反證法：先假設它們的效率 \(\eta^{'} > \eta\)，則

\[\displaystyle\frac{Q_1^{'} - Q_2^{'}}{Q_1^{'}} > \displaystyle\frac{Q_1 - Q_2}{Q_1} \qquad \qquad ② \]

可得 \(Q_2^{'} < Q_2, \ Q_1^{'} < Q_2\)。

作為復合機，結果成為外界沒有對復合機做功，而復合機卻能將熱量 \(Q_2 - Q_2^{'} = Q_1 - Q_1^{'}\) 從低溫熱源送到高溫熱源，這違背了熱力學第二定律的克勞修斯表述。所以 \(\eta^{'} > \eta\) 為不可能，只有 \(\eta \geq \eta^{'}\)。類似地令 \(E\) 作正循環帶動 \(E^{'}\) 作逆循環，可以證明 \(\eta > \eta^{'}\) 也是不可能的，只有 \(\eta^{'} \geq \eta\)。可見兩種結論相較，只有 \(\eta^{'} = \eta\) 成立。如果令 \(E\) 和 \(E^{'}\) 中任一熱機為理想氣體的可逆卡諾熱機，即 \(\eta^{'} = \eta = 1 - \displaystyle\frac{T_2}{T_1}\)。

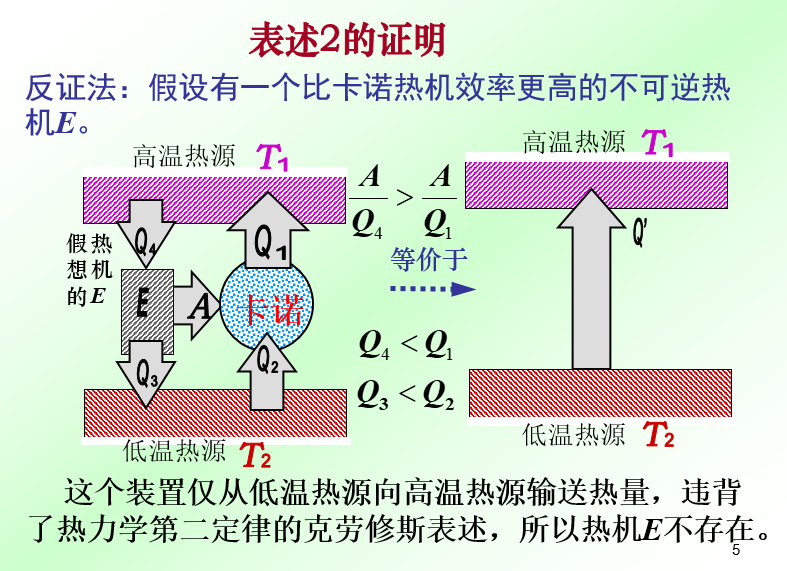
(2) 證明卡諾定理2：
如下圖所示，如果用一個不可逆機 \(E^{''}\) 來代替“證明卡諾定理1”中的可逆機 \(E^{'}\)，並用 \(E^{''}\) 推動 \(E\) 工作，按同樣方法，可以證明 \(\eta^{''} > \eta\) 是不可能的，即只有 \(\eta \geq \eta^{''}\)，由於 \(E^{''}\) 是不可逆機，因此無法證明 \(\eta \leq \eta^{''}\)，所以在相同的高低溫兩熱源間工作的不可逆機的效率不可能大於可逆機的效率。