前面已經介紹了着色的大部分內容:
- Blinn-Phong reflectance model
- Shading models / frequencies
- Graphics pipeline
- texture mapping
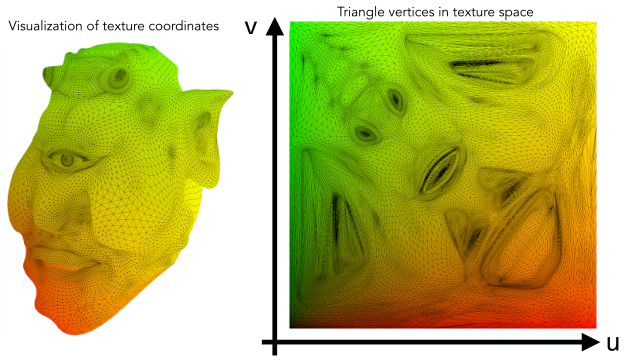
這里補充一下上一節遺漏的一丟丟知識點,見下圖。左邊是渲染后的平面圖,右邊是對應的紋理。另外無論紋理平面原始有多大,最后都會被映射在\(U-V\)坐標,又稱紋理坐標,並且規定坐標范圍是0~1。
舉例來說就是左下角為原點,它的\(U-V\)坐標是(0,0),而右上角頂點坐標則是(1,1)。例如一個256x256大小的二維紋理,UV坐標(0.5,1.0)對應的紋素坐標(128,256)。這樣一來,比如A紋理原來的大小是100x100,B紋理原來的大小是20x20,很顯然映射后A所對應的紋理平面的紋理會更密集,而B則會相對稀疏。
本節內容概要:
- Shading
- 重心坐標(barycentric coordinates)
- Texture queries
- Applications of textures
- Shadow mapping (下一節介紹)
1. 三角形內插值:Barycentric Coordinates
要介紹插值算法,首先需要知道為什么我們需要插值。其實在上一節中已經介紹過,像Phong Shading這樣的算法,它需要在已知頂點法向后對每個像素求出法向,因此需要用到插值算法,更進一步的目的是希望能夠在三角形內部獲得一個平滑的過渡。當然除了對法向做插值,我們也可以對顏色、紋理坐標等做插值計算。
那么怎么做插值呢?這就需要用到重心坐標(Barycentric Coordinates)。
注意重心坐標並不是指三角形內重心的坐標,而是每個點的坐標表示形式不再是常用的直角坐標系,而是用重心坐標來表示任意點。
1.1 重心坐標的計算
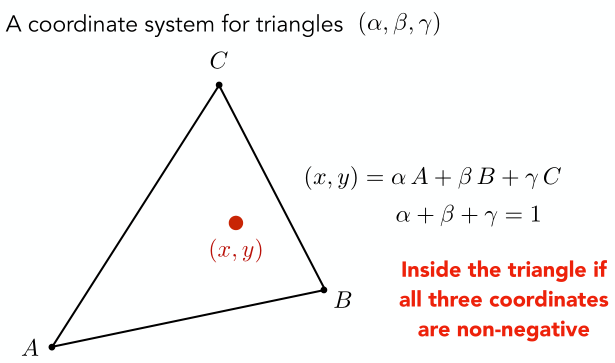
說起來有點繞,直接看下圖,下圖給出了重心坐標的示意圖。下圖中三角形三個頂點分別是A,B,C(假設是2D空間), 其中紅點可以是三角形內任意的點,該點的真實坐標為\((x,y)\),重心坐標為\((\alpha,\beta,\gamma)\),真實坐標和重心坐標滿足如下關系:即該點的直角坐標是三個頂點直角坐標的線性組合,且系數之和為1,且每個系數是非負的。
舉例來說,A點的重心坐標為(1,0,0)
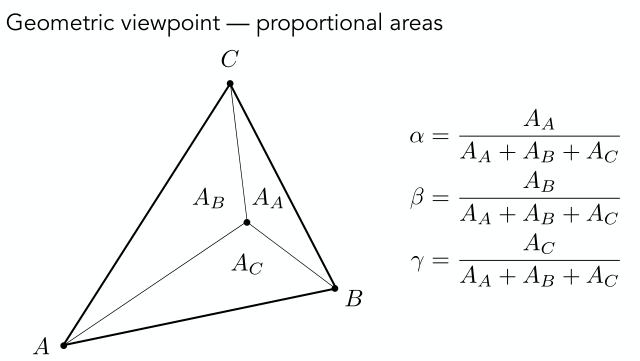
上面重心坐標的三個系數是從坐標的角度計算得到的,其實也可以從幾何角度來計算。具體來說就是計算三角形面積占比。以下圖為例,我們隨便選取一個三角形內的點,然后將三個頂點和該點連接后可以得到三個子三角形,那么三個系數計算公式如下:
\(A_A\)表示\(Area_A\)
我們知道三角形重心的直角坐標是頂點坐標的算術平均,即\(x_c=\frac{1}{3}(x_A+x_B+x_C)\),那么很自然重心的重心坐標就是\((\frac{1}{3},\frac{1}{3},\frac{1}{3})\)
基於上面的介紹,這里給出任意點的重心坐標計算公式:
1.2 重心坐標插值
介紹完了重心坐標,那我們怎么利用重心坐標來做插值呢?其實很簡單,我們首先假設三角形內每個點的重心坐標已經求解出來了,那么之后的插值計算就很自然了,因為重心坐標其實就是插值了。
舉例來說,如果我們想要求三角形內任意點\(k\)插值后的法向\(n_k\),那么首先我們一直三個頂點的法向,則\(n_k=\alpha n_A+\beta n_B + \gamma n_C\)。
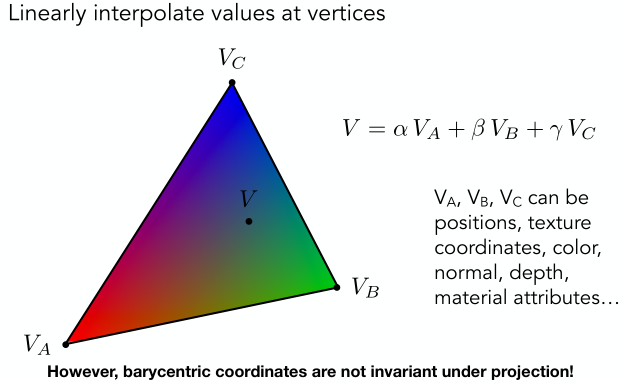
但是有一點需要注意的是,3D物體投影到2D屏幕后,點的重心坐標可能是會發生變化的,比如3D時重心坐標可能是(0.5,0.2,0.3), 到了2D后就變成了(0.4,0.4,0.2),這樣一來就可能導致差值結果產生較大偏差。所以為了避免這種偏差,正確的做法是什么呢?舉例來說,假如我們要求投影后三角形內所有點的深度信息,我們不能根據2D空間中三個頂點的深度信息做插值,而需要先計算出3D空間中的三角形內每個點的重心坐標,然后計算出3D空間中該點插值后的深度信息,最后將該深度信息填充到對應的2D位置上。
2. Simple Texture Mapping: Diffuse Color
簡單的紋理映射偽代碼如下:
我們需要遍歷每個光柵化后的屏幕采樣點(即每個像素),得到該像素的中心坐標(x,y),之后通過某種對應關系找到該像素點(x,y)在二維的紋理平面的坐標(u,v),然后得到該坐標的紋理信息(通常是漫反射系數\(k_d\)),最后將紋理信息設置到對應像素即可。

上面介紹的是一個比較粗略的紋理映射的過程,但是在這一過程中會遇到不少問題。
在介紹之前,我們需要引入一個新的概念,就是紋理元素,又簡稱紋素(texel)。我們知道像素是圖片構成的基本單元,也是屏幕空間的基本單元,大部分情況下是方的,而紋素是紋理圖片空間的基本單元,可以看成是紋理的組成“像素”,這里讓它區別於像素,主要是為了強調它的應用方式。而且像素一般是平面的(當然有體素這個),紋素則因為紋理可以是多維(一般1~3維),所以紋素是也可以是多維的。
當3d紋理物體最終繪制到屏幕上的時候,紋素會被轉換成屏幕的像素最終呈現出來。而紋素與紋素之間會以texture filtering里的規則進行填充,所以紋素也並不是指代一個點,它具體代表什么還要分情況:
- 在屏幕上可以說它指代的是屏幕上一塊區域(不一定是方的),最終呈現的是其轉換成的像素來顯示的
- 在三維物體上,它是貼圖紋理的最小單元,可以是原文紋理里的多個像素,也可以小於一個像素
在物體uv空間,它會呈現和像素一樣方式的排列,不過它的不以像素為單位,而是用uv位置表示。
Pixel和Texel的區別可以參考如下兩個圖:
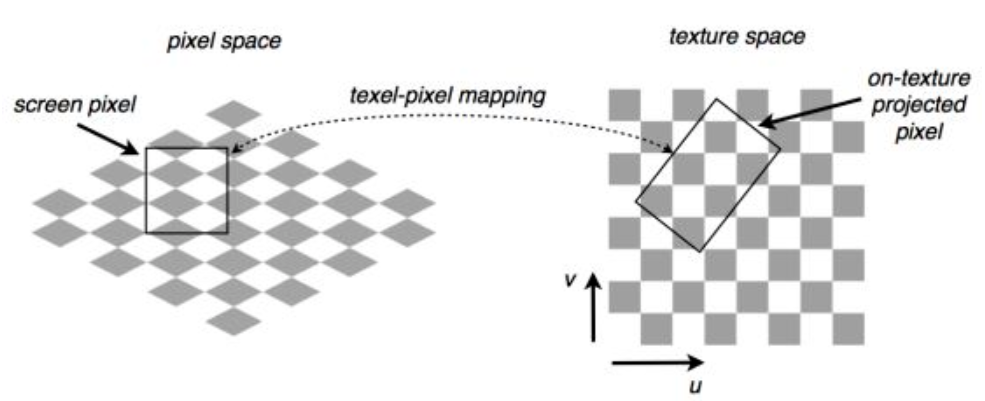
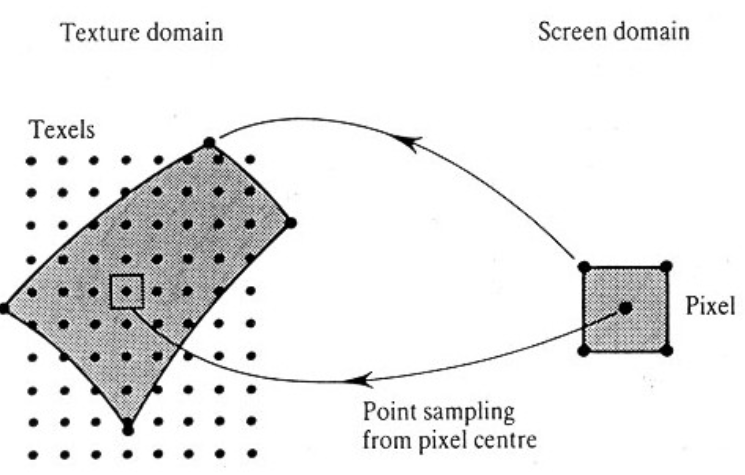
總結來說Pixel和Texel對應關系可以有如下三種:
- 一 一對應
- 一個Pixel包含多個Texel
- 一個Texel可能需要由若干個像素顯示
一 一對應是比較好的情況,余下的兩種情況則需要我們特殊處理。
2.1 Texture Magnification(紋理放大)
第一個問題就是紋理放大,就是說相對於要渲染的物體,紋理的分辨率不太高。
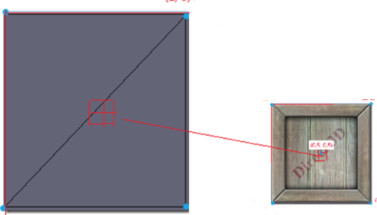
舉例解釋就是假設我們需要用右邊的紋理(比如是40x40)渲染左邊的兩個三角形(比如是80x00),但是紋理平面非常小,那么最后導致的結果就是一個紋素要對應4個像素,這樣在實際渲染時產生的效果就是紋理被拉伸,視覺上會有模糊的感覺,如下圖(左)。
2.1.1 雙線性插值
為了解決這個問題,一個常用的辦法是雙線性插值(Bilinear interpolation)。

由於要渲染的物體大於紋理平面,所以物體中的一些部分對應到紋理平面坐標可能就不是整數了,而是小數,比如下面的紅點,那此時紅點的紋理應該怎么表示呢?
一個很自然的想法是選取離紅點最近的像素點的紋理,但是這樣一來就會導致在實際渲染時,物體的某一部分的紋理是完全一樣的。
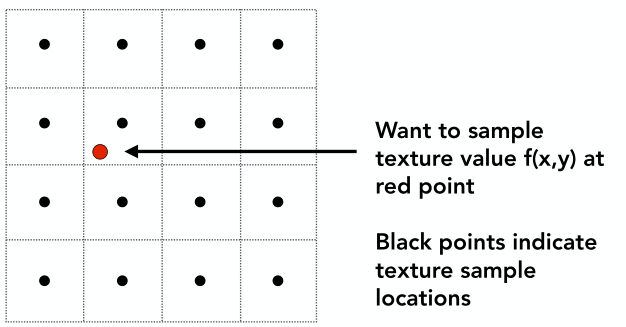
雙線性插值就是為了解決上面的問題,下面做具體介紹:
- 以紅點左下角的像素中心點作為原點可以計算出橫軸和縱軸兩個方向上的坐標\((s,t)\)。
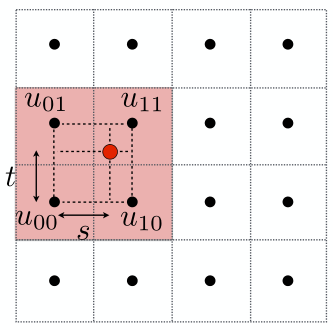
- 線性插值(linear interpolation, lerp)的計算公式為:
那么很自然,這里紅點對應到\(u_{00}\)和\(u_{10}\)之間的點\(u_0\)的值就等
\(u_{0}=lerp\left(s, u_{00}, u_{10}\right)\);同理紅點對應到\(u_{01}\)和\(u_{11}\)之間的點\(u_1\)的值就等
\(u_{1}=lerp\left(s, u_{01}, u_{11}\right)\)

- 上面已經做了線性插值求出了\(u_0,u_1\),那么很自然地,我們在\(u_0\)和\(u_1\)之間再做一次線性插值不就求解出紅點的值了嘛,即\(f(x,y) = lerp(t,u_0 ,u_1 )\)
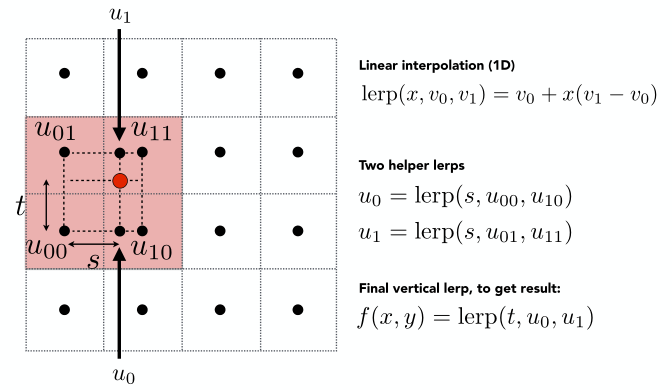
總結來說,雙線性插值其實就是橫向和縱向兩個方向做插值。
2.2 Texture Minification(紋理縮小)

另外一種情況就是紋理相比於要渲染的物體大,這樣就會導致紋理縮小,即一個像素會覆蓋多個紋素。
除了紋理分辨率大於要渲染的物體,在如下情況中也會出現紋理縮小的問題。左邊是我們要達到的效果。我們知道左邊其實通過透射投影來將物體映射到平面,因此會造成近處紋理大,遠處紋理小的視覺效果。

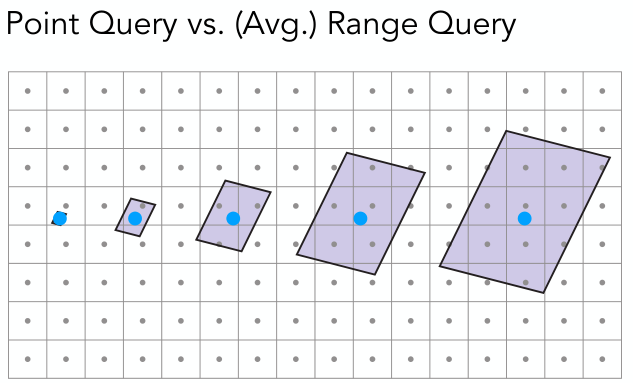
換句話說就是近處的一個像素可能只覆蓋一個紋素,或者一個紋素覆蓋多個像素(這種情況用雙線性插值可以解決),但是對於遠處的像素而言,一個像素會覆蓋多個紋素,如下圖示(藍點表示一個像素點,框表示該像素點所能覆蓋的紋素數量)。
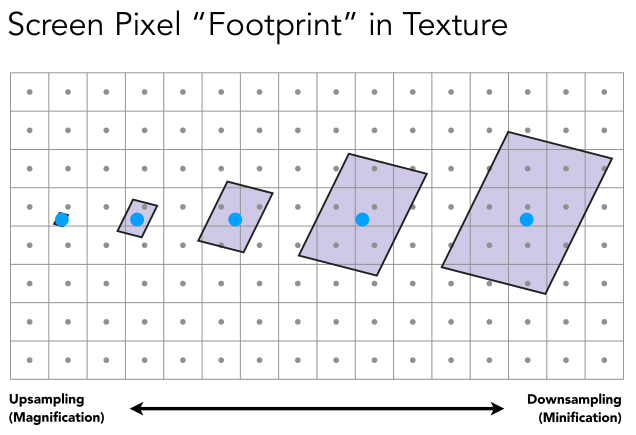
對於一個像素覆蓋多個紋素的情況,最簡單的處理辦法是首先算出某一個像素的中心點對應到紋理UV坐標,之后選擇該點的紋理來填充該像素。

但是這樣一來就會導致上圖右的失真(aliasing)問題,即產生Morie和Jaggies。原因其實就是采樣頻率過低導致的。怎么理解呢?其實我們可以把紋素數量理解成樣本數,而像素數量就是采樣頻率。當一個像素覆蓋多個紋素,那么此時紋素的數量就類似於信號中的高頻信息,而用於表征的像素數量就是采樣頻率,很顯然上面的方法采樣頻率太慢,因為只采樣了一個點(即像素中心所對應的紋素),所以導致了失真。
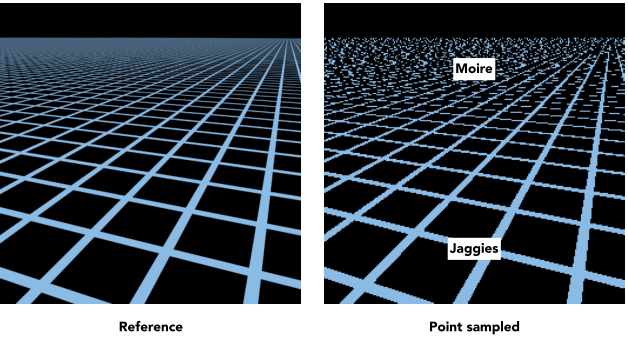
其實在前面Lecture 06已經介紹過可以用MSAA算法通過提高采樣率(將一個像素分解成若干個子像素,然后求平均)來解決失真問題,但是這樣需要大量的計算,非常耗時。
那么有沒有更好的解決辦法呢?我們知道上面之所以失真就是因為采樣導致的,那如果我們不采樣呢(滑稽)?一個思路就是我們假設對每一個像素點,我們都能求出該像素點所覆蓋的紋素的平均值,按彈幕的說法就是空間換時間。
簡單來說原來的思路是點查詢,現在變成了范圍內的平均查詢
2.2.1 Mipmap
Mipmap就是一個常用來解決紋理縮小問題的方法,它可以快速地對一個正方形內部(紋理查詢)近似查詢,注意它只能是對正方形查詢,對其它形狀還不行。
MipMap方法如下:首先它會將原始的紋理圖不斷下采樣,有點類似於卷積神經網絡里的池化操作,可以看到最開始是level 0,每下采樣一次,紋理大小就變為原來的1/4,知道最后只剩下一個紋素。下圖中得到了8層紋理。

通過上面的操作我們可以得到如下的多個不同層次的紋理圖。那么最后我們多生成了這些紋理圖,相比與原來的一個紋理圖,我們需要額外消耗多大的存儲空間呢?
這個很好計算,我們假設原紋理圖大小是1,每次下采樣后的紋理圖是原來的1/4,這其實就是等比數列,最后總的紋理圖大小是4/3,所以最后需要多消耗1/3的存儲量。
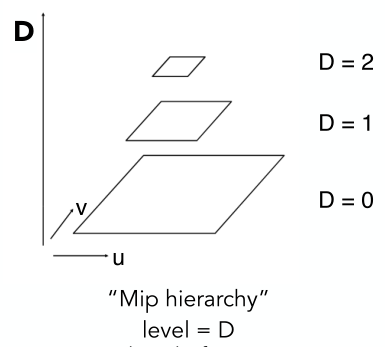
得到了不同層次的紋理圖后,我該怎么計算某一個像素點所對應的紋理呢?或者說我怎么知道某個像素點對應到哪一層紋理圖呢?
以下圖為例,假設我們要計算出三角形的紋理,首先我們可以計算出每個像素點對應到紋理UV的坐標。
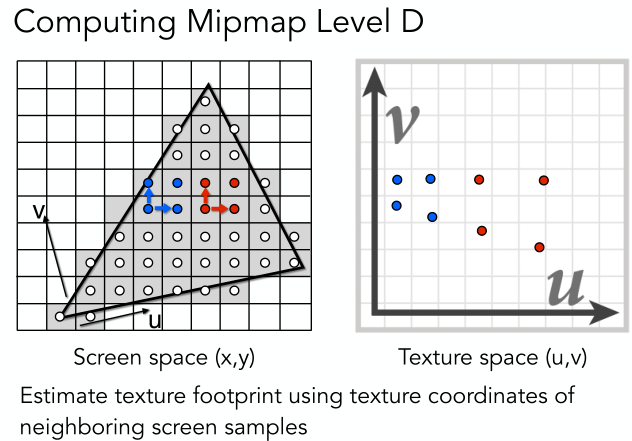
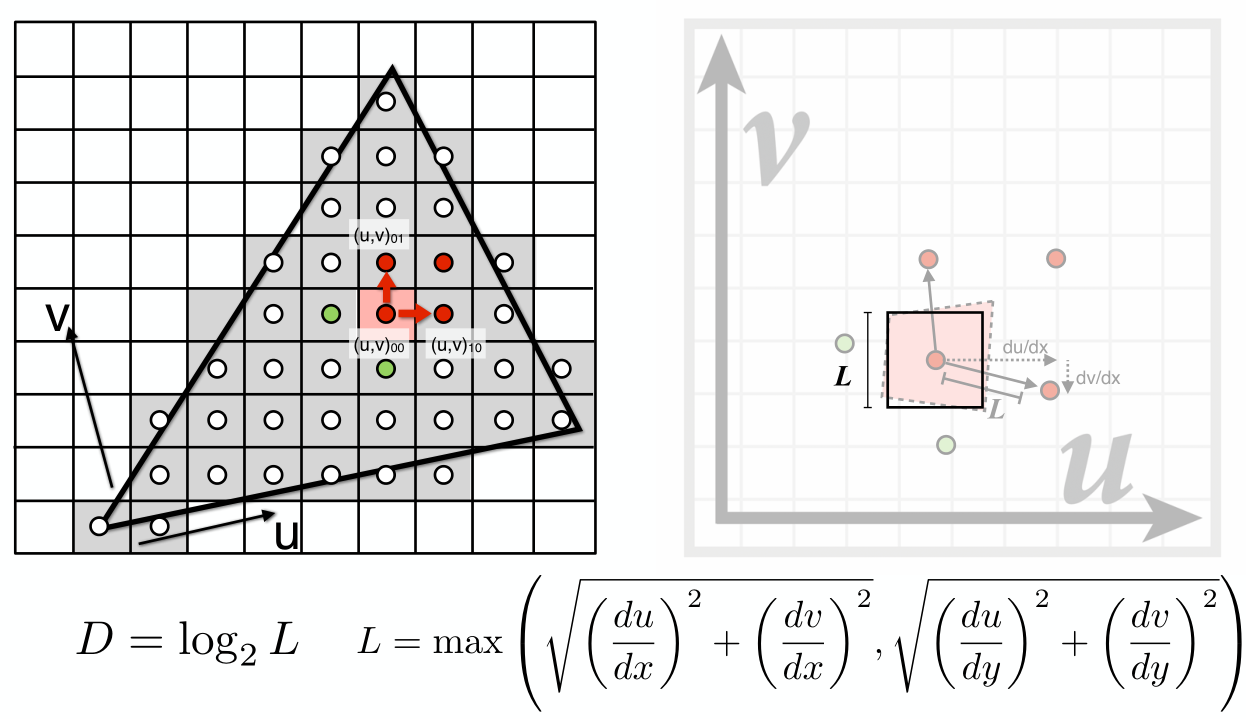
對於每個像素點我們都可以找到它的鄰居像素點所對應的UV坐標,如下圖示,其實我們也可以得到右邊那樣的不規則圖形,然后用那個圖形內部紋理的平均值作為該像素的紋理。投影后紋素點之間的距離(\(L\))計算公式為:
上面為什么要用微分還沒有太理解,這里把GAMES微信群里其他大佬的解釋放上來僅供參考:
- 想一個平面,紋理圖和屏幕分辨率一樣,但在屏幕中一個紋素可能只占了一半的像素,u,v在屏幕空間的變化就是2了。(仲唐)
- \(L\)的含義是指屏幕空間這個像素對應在紋理圖上覆蓋的區域的長度,這個L的單位是紋理圖上的紋素個數,而不是不是uv坐標上的距離。(7788)
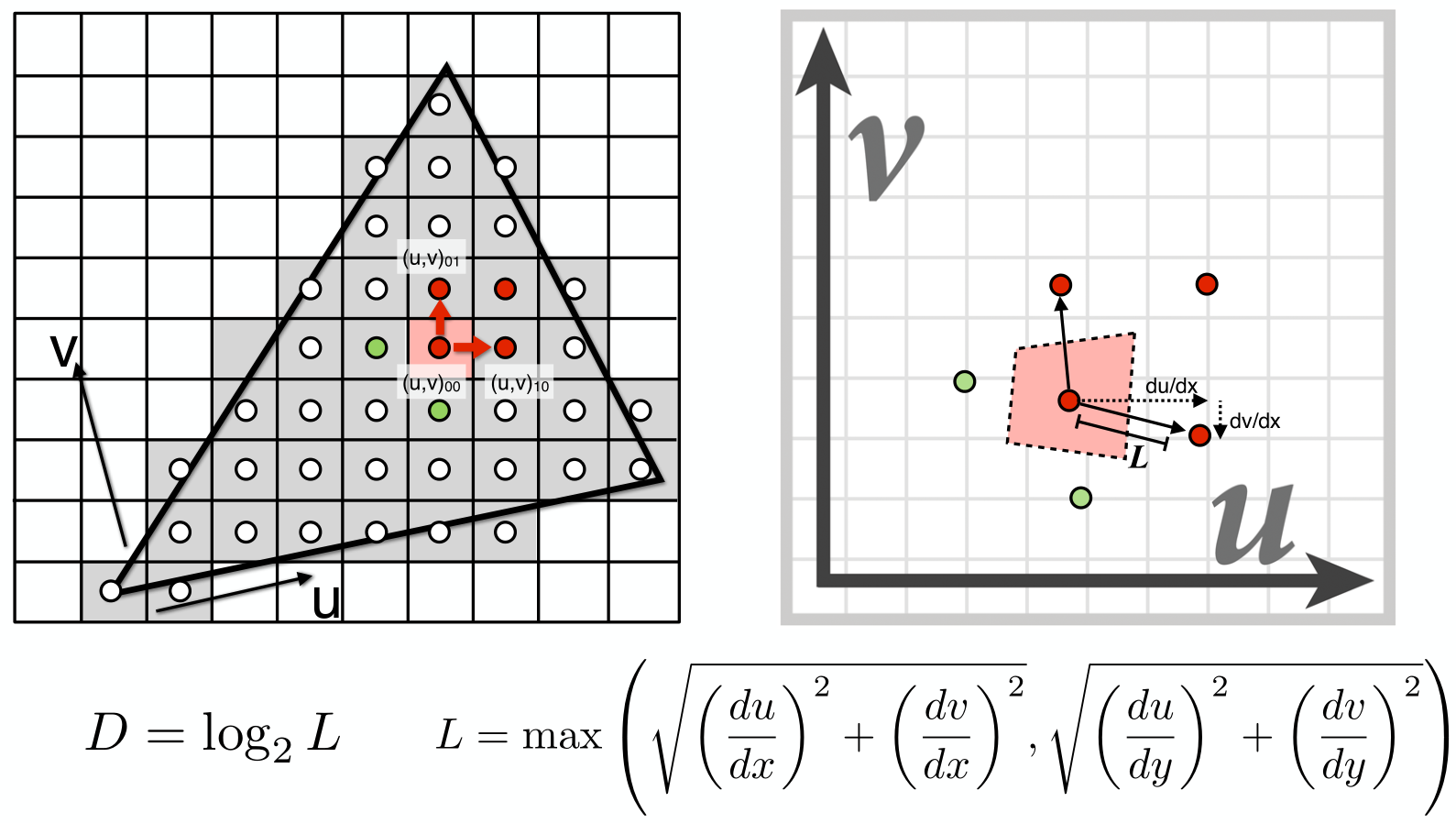
但是如果使用不規則圖形來計算紋素的平均值會復雜不少,而Mipmap的精妙之處就在於它會用正方形來近似不規則圖形,如下圖示,假設近似后的正方形邊長為\(L\),此時我們就能利用前面生成的若干層紋理圖了,我們可以很明顯的知道,這個邊長為\(L\)的正方形會對應到第\(D=log_2L\)層的紋理圖的某一個點的值,也就是說我們只需要直接查詢第\(D\)層紋理圖即可知道這個正方形的平均值了。比如如果\(L=1\),那么我們就從level 0的紋理圖去查詢就好了,而如果\(L=4\),那么我們就需要從level 2的紋理圖去查詢。
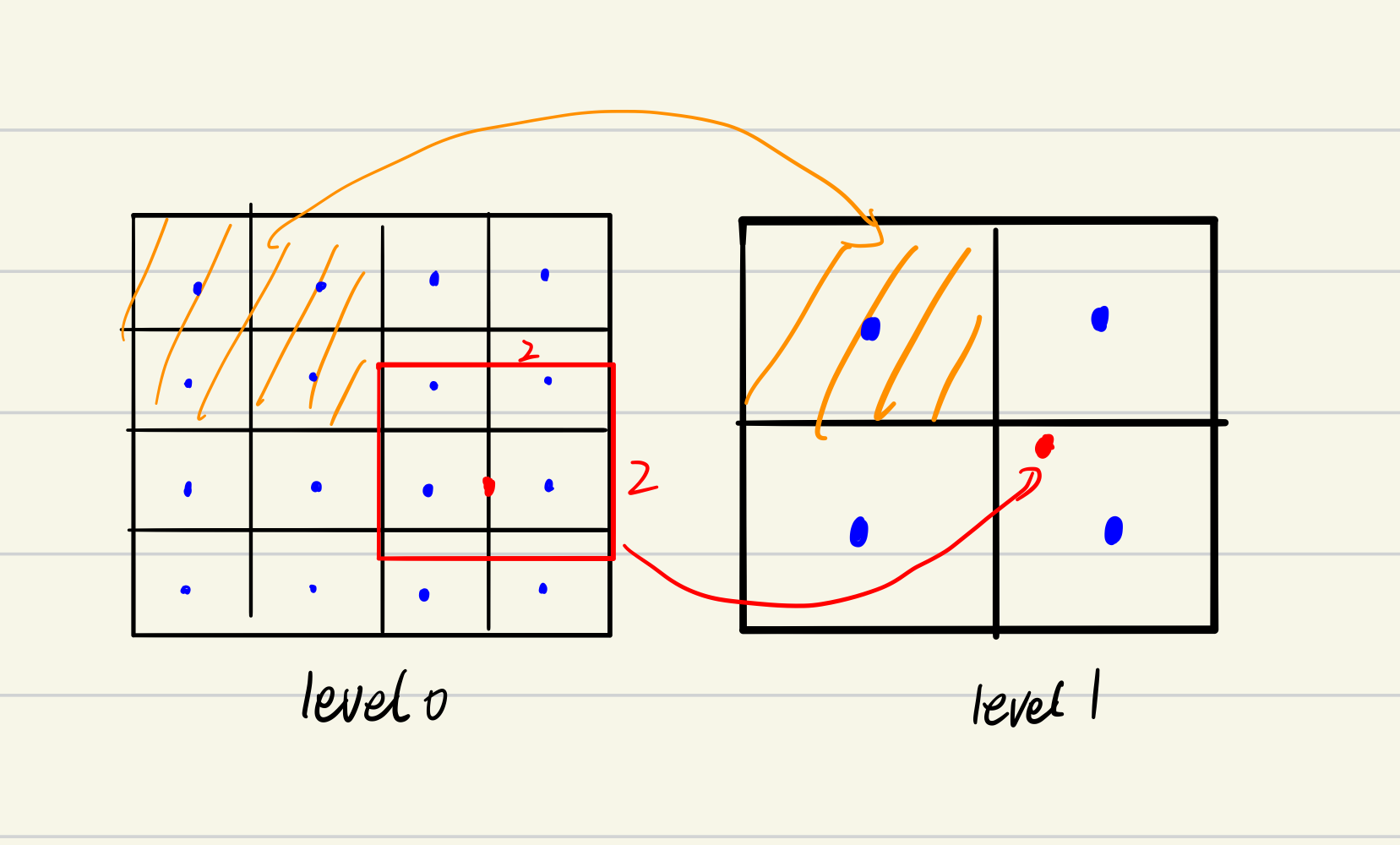
注意不同層的紋理圖最后依舊會被歸一化到0~1之間,所以只要正方形的邊長是2的指數倍,總能找到對應的點,示意圖如下:
當正方形邊長不是2的指數,比如當\(L=3\),此時\(D=log_2 3=1.58\)。
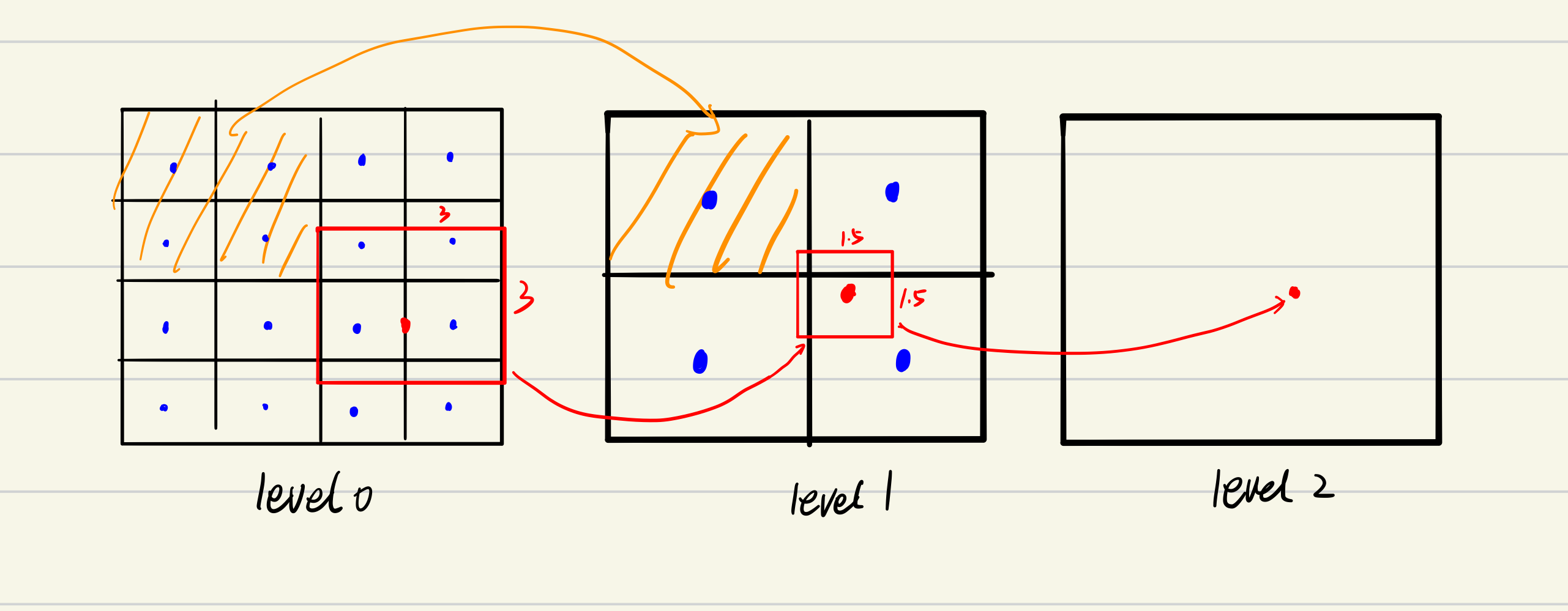
此時就需要用到三線性插值算法(Trilinear interpolation)。算法示意圖如下:在該例中,左邊應該是level 1的紋理圖,右邊是level 2 的紋理圖。紅點是原像素點在不同level映射的紋素位置,三線性插值的原理很簡單就是現在兩個level的紋理塗上先做雙線性插值求出紅點的值,然后再在層與層之間做插值,所以叫做三線性插值。
層與層之間的插值很好理解,其實也是一次雙線性插值,因為不同level的紋理圖都被歸一化到0~1之間的uv坐標,所以我們可以知道兩個層的紅點uv坐標,然根據uv坐標做一次雙線性插值即可。

2.2.2 Mipmap改進算法
至此Mipmap就算介紹完了,但是還是有些許問題需要改進。前面也提到了Mipmap其還是對正方形做的近似,
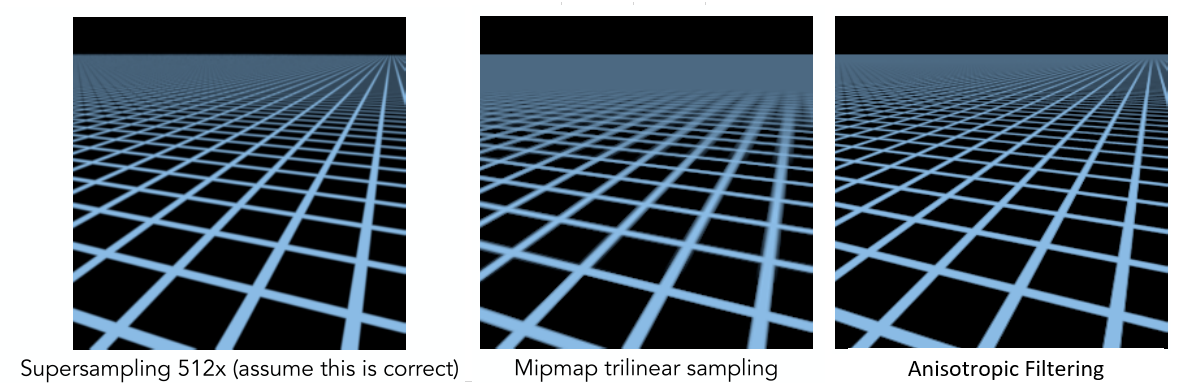
下圖(左)是超采樣的結果,看起來還是不錯的,中間是Mipmap的效果,可以看過在遠處很明顯都模糊掉了,一個改進的算法是各向異性過濾(Anisotropic Filtering),效果如圖右。
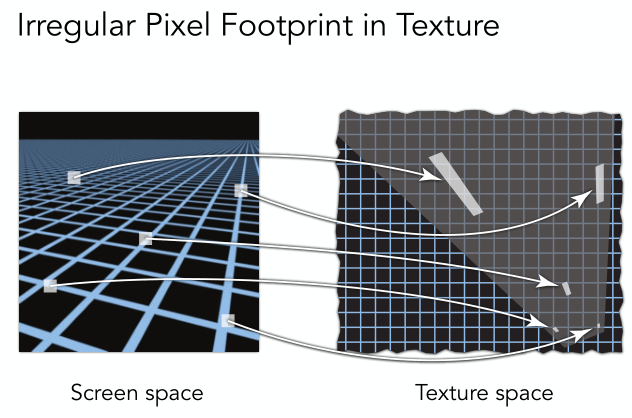
Mipmap之所以會產生模糊效果正是因為正方形近似導致的。我們通過下圖可以看到左邊的屏幕空間的每個像素對應到右邊的紋理空間的形狀可能是不規則的扁、長的形狀,如果用正方形取近似顯然會導致很大的誤差。
而各向異性過濾算法則是通過對矩形的近似來解決Mipmap的缺點,我們看下圖中的右上角的圖,圖中有很多被不同程度壓縮的衛星。Mipmap得到的一系列的紋理圖其實就是對角線上的衛星,可以看到都是正方形的,而各向異性過濾會對把原紋理圖縮放成不同大小的矩形,各向異性生成的一系列紋理圖也叫Ripmaps。
我們可以看到每一行其實就是對紋理圖做寬度的壓縮,每一列就是對紋理圖的高度做壓縮。這樣處理之后,當查詢屏幕空間某個像素點的紋理時,我們就可以用其對應的紋理圖上的紋理,這樣就解決了Mipmap只能用正方形來近似的問題。
但是各向異性過濾只是解決了規則的矩形的映射問題,還是沒法解決那些非常不規則的圖形,比如上圖的紋理圖中的斜着的矩形。而EWA Filtering就是為了解決這個問題,它的思路就使用橢圓形去近似那些不規則的圖形,然后做多次查詢來近似,雖然效果提升了,但是耗時也更長了。

