之前的課程里介紹了
- Shading 1 & 2
- Blinn-Phong reflectance model
- Shading models / frequencies
- Graphics Pipeline
- Texture mapping
- Shading 3
- Barycentric coordinates
- Texture antialiasing (MIPMAP)
- Applications of textures(本節會補充介紹)
(補充 1)Shading - applications of textures
因為上一節還有一丟丟紋理相關的內容沒講完,所以在這一節補充。
在介紹紋理的應用之前,首先還是給紋理做一個大致的概述:
- 在現代GPU中, texture=memory + range query (Filtering),即紋理其實就是存儲在GPU上的一塊內存上的數據,然后我們可以對這塊內存做區域查詢(例如MipMap)。
常用的紋理應用有如下:
- Environment lighting (環境光)
- Store microgeometry
- Procedural textures
- Solid modeling
- Volume rendering
1.1 如何表示環境光
如下圖示,通常一個光滑的表面(比如水晶球)會反射環境光,因此我們可以看到球面上會被映射出其他物體。那么計算機中如何表示這個呢?

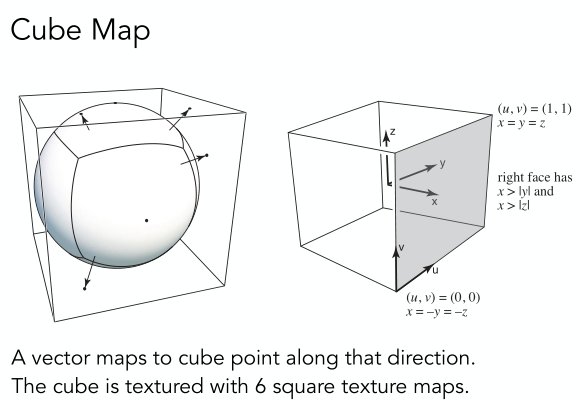
一種方法是Spherical Environment Map,即先把環境光信息記錄在球面上,其中還包括了球面與二維平面之間的映射關系。

但是上面這種方法會有一個問題,即映射到二維平面后會導致扭曲,如下圖示:

既然球面會導致扭曲,那么一種改進的思路如下,即我們不再把信息記錄在球上,而是記錄在一個立方體的表面上,這個立方體會包住原來的球體。
1.2 凹凸貼圖(法線貼圖)
我們可以看到下圖的橘子會有坑坑窪窪的感覺,那這種效果如何實現呢?-- 一種方式是構造出一種復雜的形狀來顯示出凹凸感,但是這樣實現起來會比較復雜;
- 另一種方式就是通過法線貼圖來實現,這種方法的一個大致的思路是比如紋理全部是橘色的,只不過在映射到二維平面時,我們會調整每個紋理的法向。前面我們有介紹過法線方向的改變會導致光的亮度等變換,這樣就等同於像素之間有了明暗變化,所以就有了凹凸感。

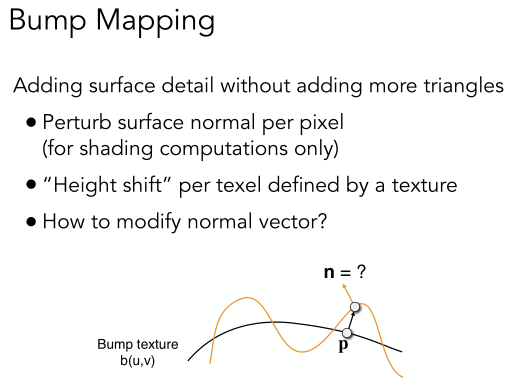
上面提到的法線貼圖方法並不需要改變任何幾何信息,即不需要增加二維平面划分成更多的三角形。那具體是怎么實現的呢?這需要用到Bump Mapping技術。
總結起來,Bump Mapping其實就是對每個像素的平面法向做了擾動。如下圖示,黑色曲線表示真實的物體光滑表面,而黃色曲線則是擾動后的效果。我們可以看到原來的P點的法向經過擾動后發生了改變,這樣就可以實現法線貼圖。那么擾動后的法向如何計算呢?
1.2.1 flatland case
首先看一下在一維情況(flatland case)下如何計算,假設下圖中的點為P點。
- P點原始的法線方向是朝上的,即\(n(p)=(0,1)\)。
- 下圖中的藍色曲線表示法線貼圖,那么P點橫向移動一個單位后,向上則會移動\(\mathrm{dp}\),(假設P點會朝着切線方向運動)。切線方向即為該點的梯度,由梯度計算公式可知\(\mathrm{dp}=\mathrm{c}^{\star}[\mathrm{h}(\mathrm{p}+1)-\mathrm{h}(\mathrm{p})]\),其中\(c\)為一個常量,所以切線可表示為\((1,\mathrm{dp})\)。
- 既然知道了切線方向,那么法線方向就很容易計算出來了,即切線方向逆時針旋轉90°即可,所以擾動后的法線方向為\(n(p)=(-dp,1).\text{normalized()}\)

1.2.2 3D case
同理在3D情況下則有兩個方向的變換,即u,v方向。
需要注意的是flatland和3D這兩種情況下我們都假設某點的法向是朝上的,所以說這個假設的法線方向其實是基於一個局部的坐標構建的,但是顯然實際情況不是這樣的。

1.2.4 Displacement mapping (位移貼圖)
上述方法其實是通過對法線方向擾動實現凹凸效果,還有一種方法是位移貼圖。
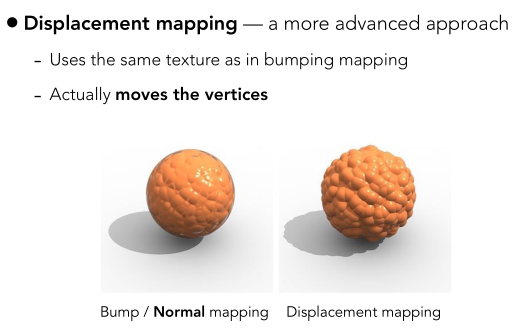
位移貼圖和法線貼圖使用的紋理是一樣的,只不過位移貼圖不再變換法線方向,而是真實地對每個三角形的頂點做一定的位移。上圖中可以看出兩種方法的區別(雖然右邊看起來有點惡心。。):
- 左邊的是法線貼圖,可以看到它並沒有改變物體形狀(還是圓形),另外影子投影結果也是一個光滑球體的投影,所以這種方法其實是一種假象,欺騙了人的眼睛。
- 右邊是位移貼圖,可以看到凹凸感很明顯,而且投影也體現出了這種凹凸感,比如凸起部位的投影也都顯示出來了。
上面的對比可以看出位移貼圖雖然效果更好,因為他需要對把物體划分成更多的三角形,即物體需要被划分的更加細致,這樣才能更准確地描述出凹凸特點,但是它的計算量也是更大的。
所以一種權衡的方式就是將二者結合起來,即首先用法線貼圖構建出一個比較粗糙的效果,然后基於這個粗糙結果,將每個三角形划分的更加小。這個在windows的DirectX庫中有提供。
1.3 三維紋理
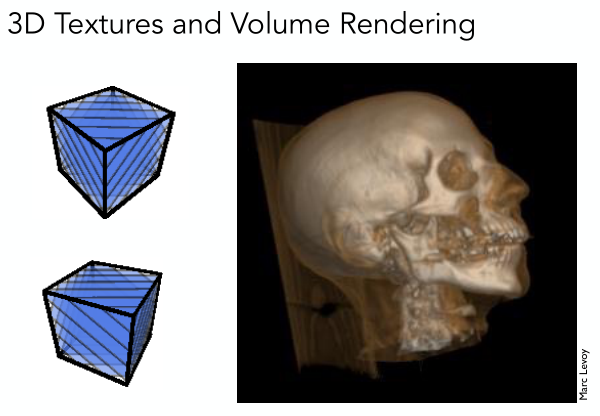
上面介紹的紋理應用都是應用在二維平面的,那么很自然就有三維的紋理應用。三維紋理的意思就是除了物體表面有紋理,物體內部也是有紋理的,而內部的紋理通常是通過生成某種三維噪聲然后再做處理得到的。比如下圖示展示的Perlin noise(柏林噪聲),就可以得到一種大理石紋理的效果。
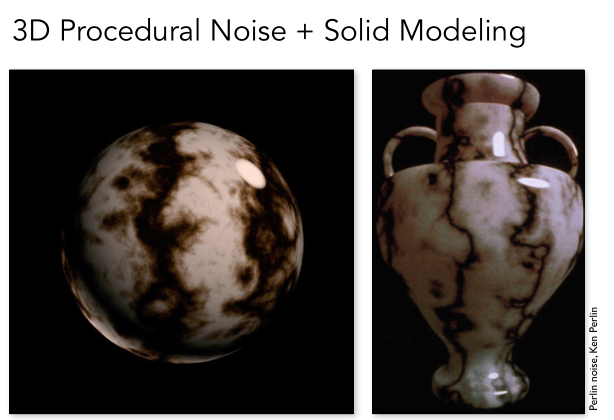
還有一種三維紋理的應用時醫學上的應用,即volume rendering(體渲染)
2. Introduction of geometry
下面正式開始介紹幾何,首先看幾個例子(右下角是亮點哈哈哈):

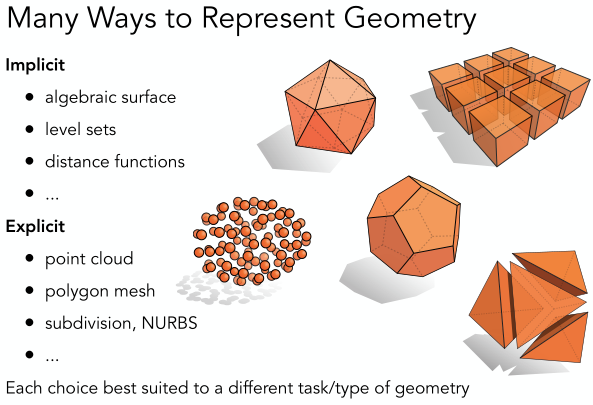
下圖給出了許多種表示幾何的方式,大體上分為顯式和隱式兩種方法。
2.1 Implicit representations of geometry
我們首先看一下什么是隱式表示。隱式表示的意思是我不會告訴你具體某個部位長什么樣子,相反我只會告訴你這個部位的點之間服從某種的關系,因此我們可以可以通過這種關系來構建幾何。
舉例來說,我們知道3D中一個球的表面上任意點坐標都滿足\(x^{2}+y^{2}+z^{2}=1\)。
更通用地表達式是\(f(x,y,z)=0\),只要滿足這個公式則表示該點在這個隱式定義的物體表面上,這也是隱式表示的一個優點。
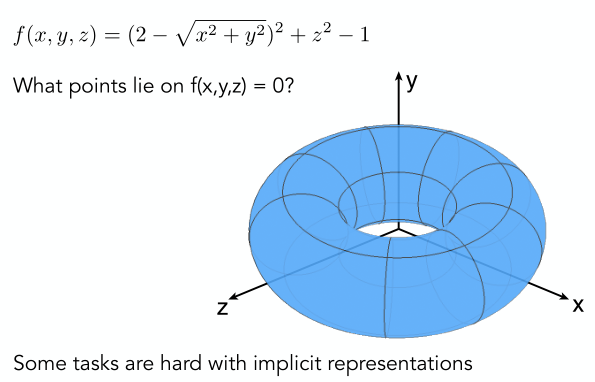
當然,隱式表示也有一個很明顯的缺點,即我們根據表達式不能直觀地知道具體表示什么形狀。比如下面的隱式表達式,如果只看式子我們根本不可能知道對應的物體的幾何形狀是什么。
- 其他有趣的式子:

- 隱式的還有一種常用的方法是constructive solid geometry(CSG),即對3D物體幾何做布爾操作,看下面的例子:
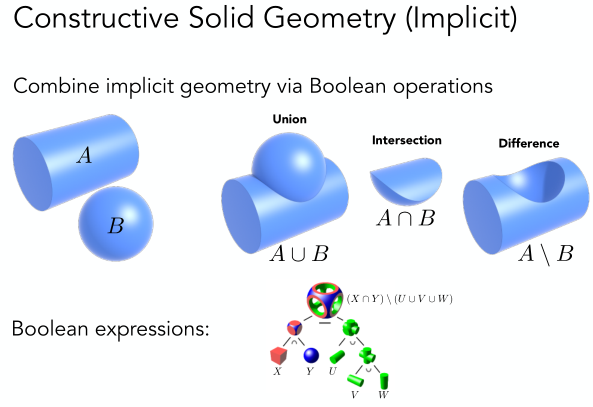
- 符號距離函數(Signed Distance Function, SDF)
還有一種隱式表示的方式是符號距離函數,這部分內容看視頻看了三遍,查了資料才明白什么意思,主要是感覺老師舉的例子並不好幫助理解,淚奔~~o(>_<)o ~~。。。
首先介紹一下這個距離函數的“距離”是什么意思,我就是被這個搞的雲里霧里的。
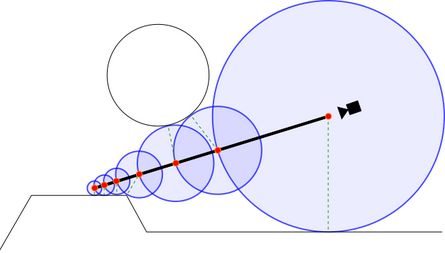
距離函數的意思是會返回當前點與任意物體表面的最短距離,如果返回的距離是負數,說明這個點在物體內部;如果為正,則在物體外部。以下圖為例,藍色圓圈表示以當前點離任意表面的最短距離作為半徑得到的圓。可以看到每次求得一個半徑后,會朝着指定方向移動這個半徑的距離,進而計算下一次的半徑,這樣可以減少距離比較的次數。
知道是什么“距離”后我們就可以利用距離函數來構造各種幾何形狀了。如下圖示(從左往右看),最開始是由兩個球,我們知道每個球都對應了一個距離函數,假設為\(d_1,d_2\)。你可能對這個距離函數還是不太理解,我們再進一步解釋,以\(d_1\)為例,假設最左邊上面那個球的中心坐標是\((x_1,y_1,z_1)\),半徑為\(r\),那么\(d_1=(x-x_1)^2+(x-x_1)^2+(x-x_1)^2-r^2=0\)。
那么我們只要將兩個距離函數做一個融合(blending),隨着融合程度的調整,我們可以得到右邊一系列的幾何圖形,給人一種兩個水滴合在一起的感覺。
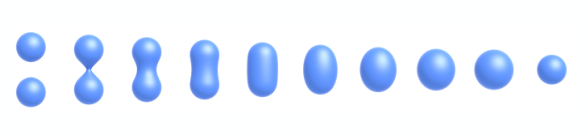
- level set methods
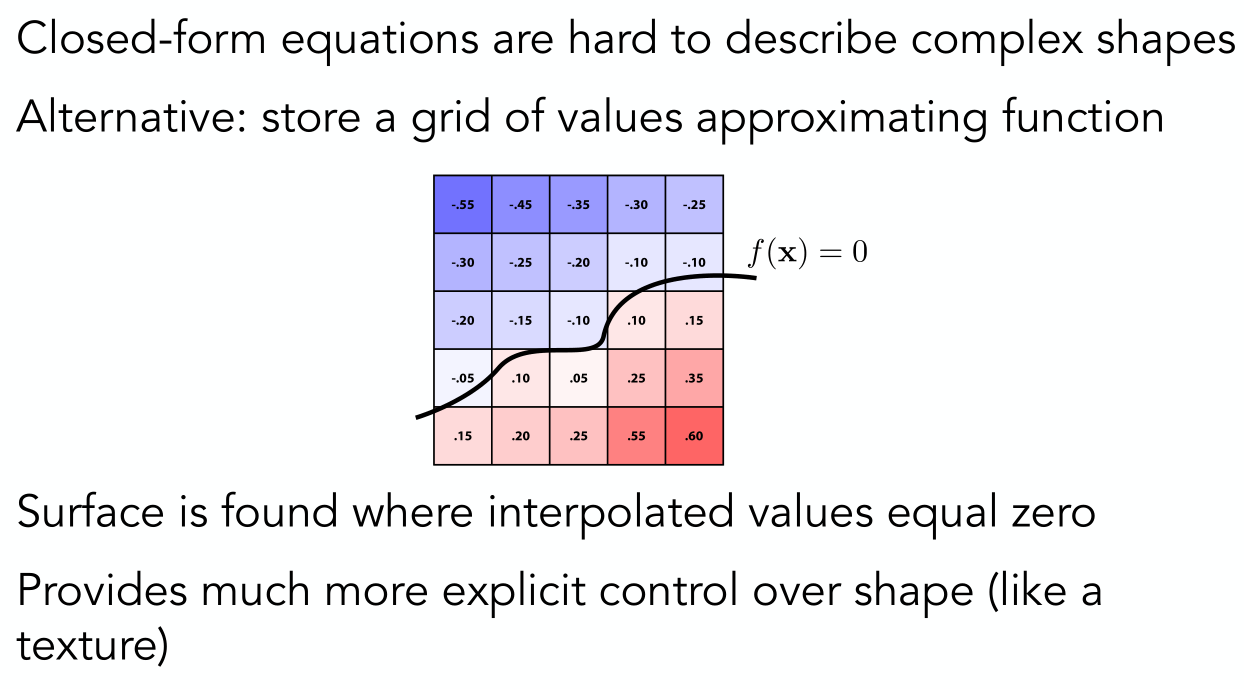
上面的距離函數需要定義出一個解析表達式,但是有時候我們不一定能夠求出這個解析式。那么針對這種情況我們可以用level set(水平集)來表示幾何形狀。
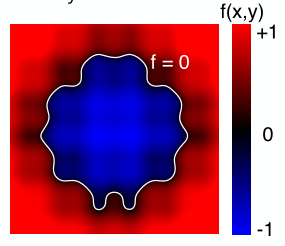
我們看下面的例子來解釋什么是level set。其實就是我們給每個格子設定一個值,然后找出值為的地方連起來就得到了level set,連接起來也就形成物體表面。
上面例子是在2D平面的levelset,我們也可以在3D上生成level set,這在醫學數據上用的比較多。此時的一個大致思路是我們給三維定義出一個密度level set,因為不同器官組織的密度是不一樣的,那么我們通過選取不同的levelset,也就得到了不同的器官或組織的表面形狀了。
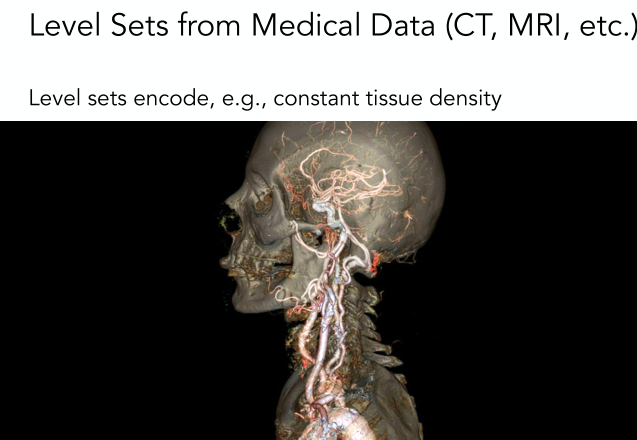
- fractals(分形)
還有一種表示方式是分形,現實生活中像雪花就是一種分形。比如它整體看起來是個六邊形,然后我們細看每條邊又是一個六邊形。其他例子如下圖示:

2.2 Explicit representations of geometry
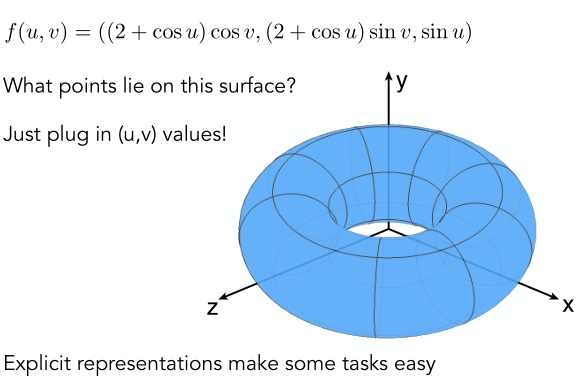
另外一種表示方式則是顯式表示。如下圖示,我們會構建一個映射函數,這個函數會將左邊的二維的平面圖的每個點都映射到右邊的三維幾何圖上。

還是用上面的例子來解釋顯式表示,可以看到這里的映射函數是
這里和上面的\(f(x,y,z)=0\)不一樣,因為這里我們是直接將二維uv坐邊上的某個點的左邊通過某種映射關系直接映射到三維某個具體的坐標點了,所以這是顯示的。我們只需要對二維平面上所有點遍歷一遍即可得到映射后的幾何形狀,而前面介紹的隱式方法則需要我們根據等式來判斷而為上的某個點是否在映射后的幾何物體表面。這個區別需要區分開來。
很自然地,顯式的缺點對應着隱式的優點,即判斷一個點在物體表面內部或者外部就變得麻煩一些了。
2.3 表示方式總結
| 方法 | 優點 | 缺點 |
|---|---|---|
| 顯式表示 | 很容易計算出每個點映射位置,直接得到映射物體的幾何形狀 | 不能直接判斷某個點是在映射物體的內部還是外部 |
| 隱式表示 | 無法直接知道映射后的物體的幾何形狀 | 很容易判斷二維某個點在映射后是在物體的內部還是外部 |
由上表可以知道目前還沒有一種最優的表示方式,只能依靠需求來選擇合適的方法。
