【GAMES101-現代計算機圖形學課程筆記】Lecture 04 Transformation Cont.

1. 3D Transformations

這里再上一節內容的基礎上對3D 變換做個補充說明

3D下點和向量表示如下：

• 3D point \(=(x, y, z, 1)^{\top}\)

• 3D vector \(=(x, y, z, 0)^{\top}\)

• Scale

\[\mathbf{S}\left(s_{x}, s_{y}, s_{z}\right)=\left(\begin{array}{cccc} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)\]

• Translation

\[\mathbf{T}\left(t_{x}, t_{y}, t_{z}\right)=\left(\begin{array}{cccc} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{array}\right)\]

• Rotation

• 繞x軸旋轉

\[\mathbf{R}_{x}(\alpha)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)\]

• 繞z軸旋轉

\[\mathbf{R}_{z}(\alpha)=\left(\begin{array}{cccc} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)\]

• 繞y軸旋轉(需要注意此時sinα的符號和前面兩種情況略有不同)

\[\mathbf{R}_{y}(\alpha)=\left(\begin{array}{cccc} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)\]

那么總的旋轉可表示如下（稱作Euler angles）：

\[\mathbf{R}_{x y z}(\alpha, \beta, \gamma)=\mathbf{R}_{x}(\alpha) \mathbf{R}_{y}(\beta) \mathbf{R}_{z}(\gamma) \]

Euler angles常用在飛機的旋轉，即旋轉划分成roll,pitch,yaw三個操作。

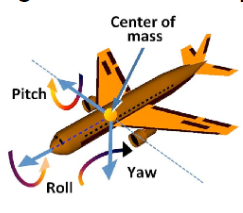
Rodrigues’ Rotation Formula
\(n,\alpha\)分別表示旋轉軸向量和角度

\[\mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc} 0 & -n_{z} & n_{y} \\ n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0 \end{array}\right)}_{\mathrm{N}}\]

2. Viewing (觀測) transformation

2.1 View (視圖) / Camera transformation

什么是視圖變換呢？

下面以拍照為例進行介紹

• Find a good place and arrange people (model transformation)
• Find a good “angle” to put the camera (view transformation)
• Cheese! (projection transformation)

2.1.1 相機的定義

那么相機需要定義如下幾個向量：

• position \(\vec{e}\): 即我的相機擺在什么位置
• look-at / gaze direction \(\hat{g}\): 即相機的朝向
• up direction \(\hat{t}\): 表示相機鏡頭擺放方向，比如我們可以把相機橫着拍，也可以正着拍。（自動腦補一下有時候攝像師為了拍攝好看的照片各種騷姿勢）

一般來說我們希望相機始終位於原點，而且相機是正擺放的(Y軸正方向)，拍攝方向是朝着正前方拍的(Z軸負方向)。

假設攝像機的初始狀態如右上角坐標所示，我們首先需要將其變換到左下角的坐標上去。

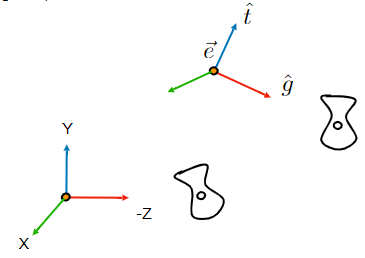
2.1.2 矩陣變換

那么矩陣形式如何表示呢？前面內容講過，我們可以先把相機平移到原點，然后再做線性變化，表示如下：

\[M_{\text {view}}=R_{\text {view}} T_{\text {view}} \]

• 平移到原點

\[T_{v i e w}=\left[\begin{array}{cccc} 1 & 0 & 0 & -x_{e} \\ 0 & 1 & 0 & -y_{e} \\ 0 & 0 & 1 & -z_{e} \\ 0 & 0 & 0 & 1 \end{array}\right]\]

• 旋轉

將 \(\hat{g}\) 旋轉到 \(-Z\), \(\hat{t}\) 旋轉到 \(Y\), \(\hat{g}\times \hat{t}\) 旋轉到 \(X\)。但是直接求這個旋轉變換有點困難，所以一個討巧的辦法是我們求逆變換，即我們先求\(Z\) 旋轉到 \(\hat{-g}\)，\(Y\) 旋轉到 \(\hat{t}\)，\(X\) 旋轉到\(\hat{g}\times \hat{t}\) ，此時逆旋轉變換矩陣如下：

\[R_{v i e w}^{-1}=\left[\begin{array}{cccc} x_{\hat{g} \times \hat{t}} & x_{t} & x_{-g} & 0 \\ y_{\hat{g} \times \hat{t}} & y_{t} & y_{-g} & 0 \\ z_{\hat{g} \times \hat{t}} & z_{t} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\]

上一節中有介紹旋轉矩陣是正交矩陣，而正交矩陣的性質是\(A^T=A^{-1}\)，那么要求的的旋轉變換矩陣，我們只需要對逆變換矩陣做轉置即可求得：

\[R_{v i e w}=\left[\begin{array}{cccc} x_{\hat{g} \times \hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \\ x_{t} & y_{t} & z_{t} & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\]

注意上面的\(x_{\hat{g} \times \hat{t}} , y_{\hat{g} \times \hat{t}} , z_{\hat{g} \times \hat{t}},x_t\)等是view坐標系下的坐標值，而不是在世界坐標系(\(XYZ\))。

總結： 介紹了這么多，我們為什么要大費周折的做這些變化呢？模型中的有很多頂點，這些頂點坐標是模型空間下的，而我們通常做變化都是以世界坐標為基准的，所以我們需要做模型變換。

2.2 Projection (投影) transformation

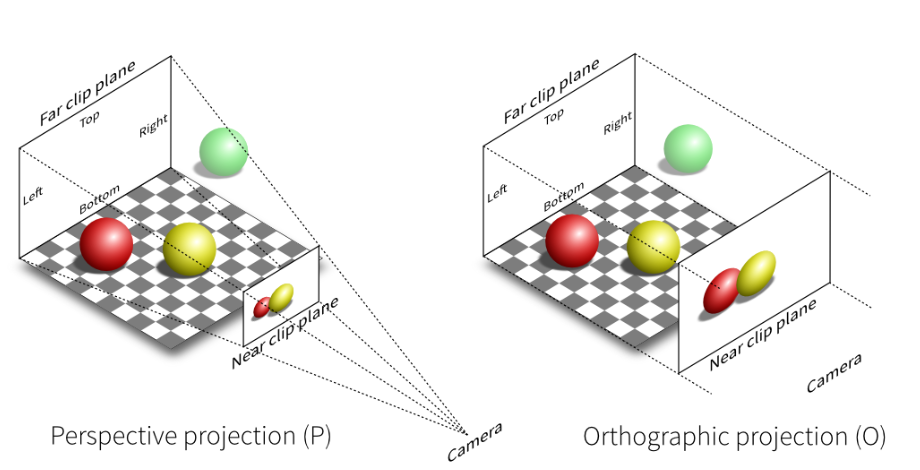
投影變化有兩種實現方法，分別是正交投影和透視投影，示意圖如下：

2.2.1 Orthographic (正交) projection

• 一個簡單的理解方式

對於正交投影而言，結合下圖來理解，相機位置放在原點，朝着\(-Z\)方向拍攝，相機正向擺放，即沿着\(Y\)方向，那么投影之后得到的東西在X-Y平面上，換句話說就是把Z軸丟掉了。不過有一點需要注意的是，投影之后一般還會把投影圖像縮放成一個邊長為2的正方形，即\([-1,1]^2\),這種做法是約定俗成的，另外也是方便后面的操作。

你可能會想問，這樣做不是會把物體做了拉伸了嗎？沒錯是拉伸了，所以一般在后面的操作中還會再做一次拉伸來還原的。

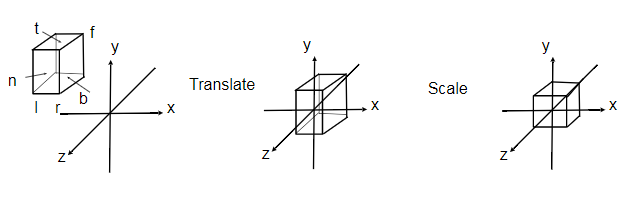
• General 操作步驟

我們有一個長方體(cuboid),表示為 \([l,r] \times [b,t] \times [f,n]\)，其中\(l,r\)表示在X軸上的左(left)右(right)頂點坐標值，同理\(b,t\)表示Y軸上的下(bottom)上(top)坐標,而\(f,n\)表示Z軸上遠(far)近(near),這個需要注意的是因為我們默認相近朝着Z軸負方向，所以Z軸坐標值越大，表示越近，反之越遠。

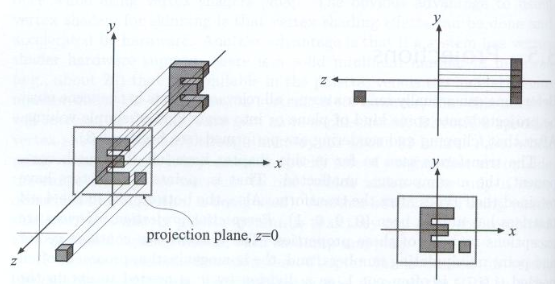
確定了長方體的表示后，我們需要做如下處理（同上面一樣），即將長方體映射為canonical cube(正則、規范、標准正方體)，表示為\([-1,1]^3\)。

具體實現方法則是將長方體中心先平移到原點，然后再做縮放變換即可，用矩陣表示如下（下式中的\(r,l\)等表示坐標值，不是向量。）：

\[M_{\text {ortho}}=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right]\]

OpenGL 采用的是左手系，所以上面式子中的負號可能相反但不影響理解。

2.2.2 Perspective (透視) projection

在介紹透視投影之前，需要介紹如下齊次坐標的一個性質：

對於3D齊次坐標內的一個點\((x,y,z,1)\)，我們任意乘以一個非零常數\(k\),得到的點\((kx,ky,kz,k)\)仍然表示同一個點。比如\([1,0,0,1]\)和\([2,0,0,2]\)表示的是同一個點\((1,0,0)\)。

下圖給出了透視投影(frustum,平截頭體)和正交投影的投影例子(Cuboid)。

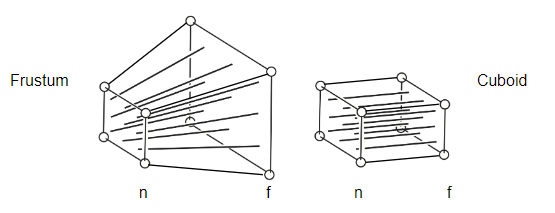
可以看到透視投影其實就是將右邊平面(即(\(f\))遠平面)的東西投影到左邊平面（即近(\(n\))平面），所有投影的線最后都相交於一個點，即視點。而正交投影的投影線互相之間是平行的。

很多教材在介紹透視投影時都是硬生生地給出遠平面投射到近平面的公式，這樣非常不利於理解。為了方便理解，我們可以把這個投影拆成兩步：

1. 我們先將遠平面以及中間的那些平面做擠壓（squish）（可以想象成把平面的四個頂點往平面的中心點靠攏，使得邊長和近平面長度相等）；注意擠壓是對所有平面所做的操作。

2. 之后我們再對擠壓后的平面再做正交投影即可。

上面第一步驟中的擠壓需要滿足如下幾個條件

• 近平面上任何一個點永遠不變。
• 遠平面擠壓前后的Z值都保持為\(f\)不變
• 遠平面的中心點X,Y,Z坐標保持不變

注意遠近平面之間的點在做變換之后的Z軸坐標可能是會變的！！！只有遠近平面上的點的Z坐標才保持不變（原因在下一講介紹），這個特別重要，后面計算會用到。

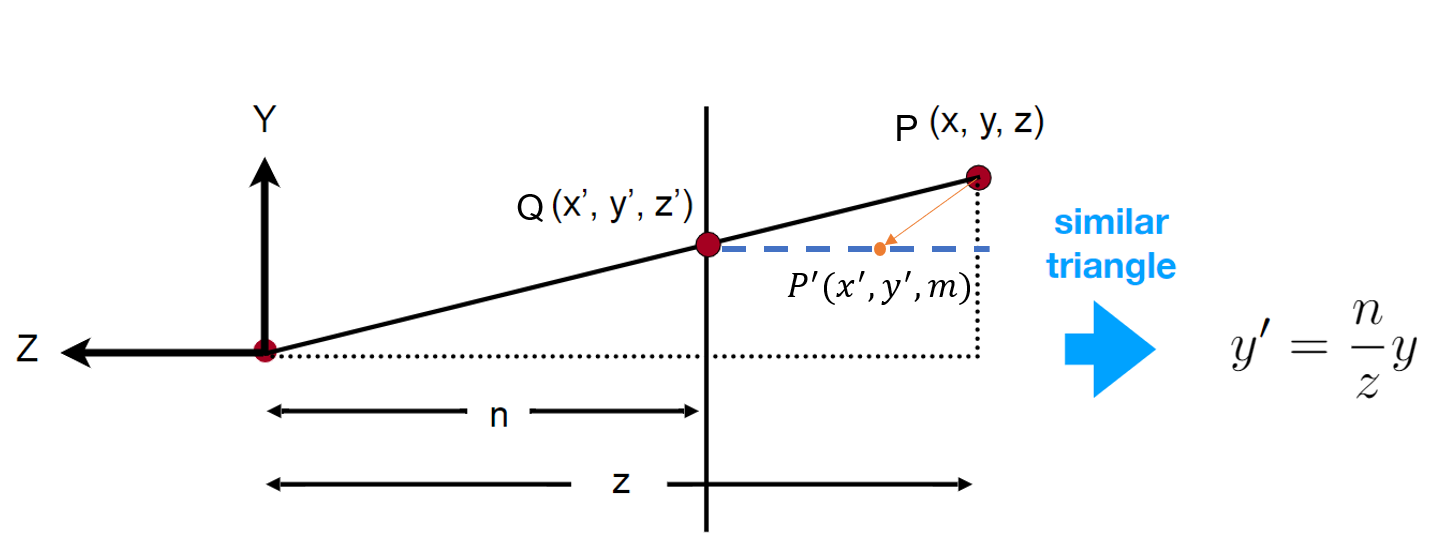
下面我們從側面來觀察遠近平面投影特點（看視頻的時候我一直以為Q點是P點擠壓后得到的點，其實P'才是，Q是P'在近平面上的投影點）：

original point坐標為\(P=(x,y,z)\),transformed point（即擠壓之后的點）坐標為\(P'=(x',y', m)\),而\(Q\)是\(P'\)在近平面上的投影點，即二者的X、Y坐標值相等，Z軸坐標不相等。近平面Z軸坐標為\(n\)，遠平面為\(f\)。

注意下圖中的\(P\)表示遠近平面上以及之間的任意點，擠壓后的\(P'\)的Z軸坐標可能與原坐標並不相等，即\(m\)不一定等於\(z\)！！！

但是我們根據相似三角形可以得到擠壓后的點Y軸坐標等於\(Q\)點的Y軸坐標，即\(y^{\prime}=\frac{n}{z} y\)，同理在X軸上的坐標為\(x^{\prime}=\frac{n}{z} x\),而坐標\(m\)暫不可知。

根據上面的分析可以得到在齊次坐標系下原坐標的變換過程如下(下面最右邊的等價是由點的定義得到的，即點坐標乘以一個常數后仍然表示原來的點。)：

\[\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right) \Rightarrow\left(\begin{array}{c} n x / z \\ n y / z \\ m \\ 1 \end{array}\right) \begin{array}{c} \text { mult. } \\ \text { by z } \\ == \end{array}\left(\begin{array}{c} n x \\ n y \\ zm \\ z \end{array}\right) \]

對點坐標的擠壓其實等價於左乘一個變換矩陣，等式如下

\[M_{p e r s p \rightarrow o r t h o}^{(4 \times 4)}\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right)=\left(\begin{array}{c} n x \\ n y \\ zm \\ z \end{array}\right) \]

至此可以求得左邊矩陣的值為

\[M_{p e r s p \rightarrow o r t h o}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ A & B & C & D \\ 0 & 0 & 1 & 0 \end{array}\right)\]

由於擠壓后的點的Z坐標\(m\)並不知道，所以上面矩陣的第三行的值都不能確定，所以用變量\(A,B,C,D\)表示。而要求解第三行的值則需要用到最開始提到的幾個需要滿足的條件：

1. 近平面上的點保持不變，即擠壓前后Z坐標值\(z=m=n\),即有

\[M_{p e r s p \rightarrow o r t h o}^{(4 \times 4)}\left(\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right)=\left(\begin{array}{c} n x \\ n y \\ zm \\ z \end{array}\right)=\left(\begin{array}{c} n x \\ n y \\ n^2 \\ n \end{array}\right)\]

進一步求解可得：

\[\begin{aligned} &A x+B y+C z+D=m z\\ &\stackrel{m=z=n}{\longrightarrow} A x+B y+C n+D=n^{2} \\ &\Rightarrow\left\{\begin{array}{l} A=B=0 \\ C n+D=n^{2} \end{array}\right. \end{aligned}\]

此時仍然求解不出來，所以我們還需要用到前面的條件

2. 遠平面的點的Z坐標保持不變，即\(z=m=f\),同理可求得等式：

\[\begin{aligned} \left\{\begin{array}{l} A=B=0 \\ C f+D=f^{2} \end{array}\right. \end{aligned} \]

現在只需要求解方程組即可，

\[\left\{\begin{array}{l} C n+D=n^{2} \\ C f+D=f^{2} \end{array} \rightarrow\left\{\begin{array}{l} C=n+f \\ D=-n f \end{array}\right.\right.\]

至此我們就完成了第一步驟求解出了擠壓矩陣，

\[M_{p e r s p \rightarrow o r t h o}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{array}\right)\]

通過上面的擠壓矩陣，我們把原來的frustum擠壓成了一長方體，那么很自然地第二步驟其實就是使用正交投影即可，而正交投影矩陣前面已經介紹了，所以最終的透視投影矩陣求解公式如下：

\[M_{p e r s p}=M_{o r t h o} M_{p e r s p \rightarrow o r t h o} \]

微信公眾號：AutoML機器學習
MARSGGBO♥原創
如有意合作或學術討論歡迎私戳聯系~
郵箱:[e-mail] 2020-04-25 11:01:24