上一節介紹了如下內容:
Viewing (觀測) transformation
- View (視圖) / Camera transformation
- Projection (投影) transformation
- Orthographic (正交) projection
- 平移到原點
- 縮放成\([-1,1]^3\)的立方體
- Perspective (透視) projection
- 將frustum擠壓成長方體
- 運用正交投影得到\([-1,1]^3\)的立方體
- Orthographic (正交) projection
具體來說上一節其實就是介紹了如何把3D空間物體變換為一個大小\([-1,1]^3\)的立方體內,那么下一步所要做的事情(把立方體畫在屏幕上,即光柵化)就是這一節所要介紹的。
1. Perspective Projection
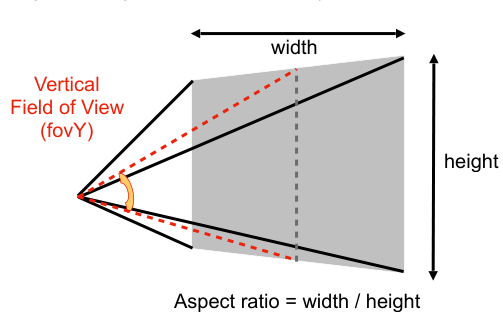
下圖灰色平面表示近平面,可由四個變量表示\((l,r,b,t)\),另外假設近平面是對稱的,即\(l=-r,b=-t\)。下面引出如下幾個定義:
- Aspect ratio = width / height
- width和height指的是近平面的寬、高
- Aspect ratio即為寬高比,比如手機的 4:3或者 16:9的比例
- Vertical Field of View (fovY): 垂直可視角度。即下圖中兩條紅線之間的角度。
下面給出了垂直可視角度的側面可視圖(只畫出了上半部分):
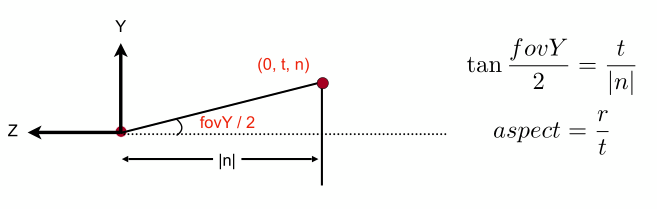
fovY和aspect 與 \((l,r,b,t)\)的關系如下:
2. Canonical Cube to Screen
MVP表示Model transformation (placing objects),
View transformation (placing camera),Projection transformation的首字母縮寫。MVP之后我們需要把Cuboid轉化到屏幕上去。
2.1 What is Screen?
Raster在德語中就是screen的意思。
Rasterize表示drawing onto the screen
Screen is an array of pixels, its size is called resolution.
2.2 屏幕空間
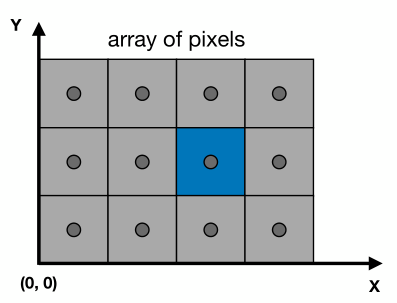
屏幕空間定義如下:
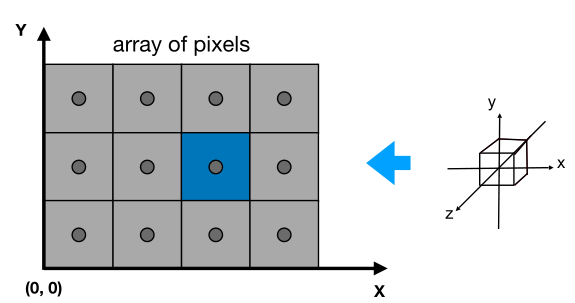
- 原點位於左下角,坐標值為(0, 0)
- 每個像素坐標值由(x,y)表示,且x,y均為整數
- 每個像素其實是一個小方框,像素中心點其實是(x+0.5,y+0.5)
- 屏幕覆蓋范圍是 (0,0) ~ (width, height)
下圖中藍色像素坐標值為(2,1),其中心點坐標為(2.5,1.5)
將cuboid變換到屏幕空間
下面介紹如何將\([-1,1]^3\)的立方體變換到屏幕空間。
- 第一步是將cuboid拉伸到和屏幕一樣的aspect ratio。注意此時我們先不管Z軸方向,只是把XY平面做拉伸,即將\([-1,1]^{2}\) 轉化為 [0, width ]x[0, height]。因為cuboid邊長為2, 所以先除以2,再對應乘上width或者height,Z軸不用管,所以參數為1 (見下面的矩陣)。
- 第二步是平移。因為拉伸前后的中心點在屏幕的原點(即屏幕左下角頂點),而我們要想在屏幕上完美展示,應該把中心點移到屏幕的中心點(以上圖為例,即為\((2.5, 1.5)\))。
那么最終的視口變換(viewport transform)矩陣表示如下:
3. Rasterization (光柵化)
光柵化是將向量圖形格式表示的圖像轉換成位圖以用於顯示器或者打印機輸出的過程。
Rasterisation (or rasterization) is the task of taking an image described in a vector graphics format (shapes) and converting it into a raster image (a series of pixels, dots or lines, which, when displayed together, create the image which was represented via shapes).
前面已經介紹了如何將空間中的物體變換成屏幕上的一個多邊形,而實際上多邊形的表示還可以進一步划分,即用一些基礎的多邊形來表示復雜的多邊形。
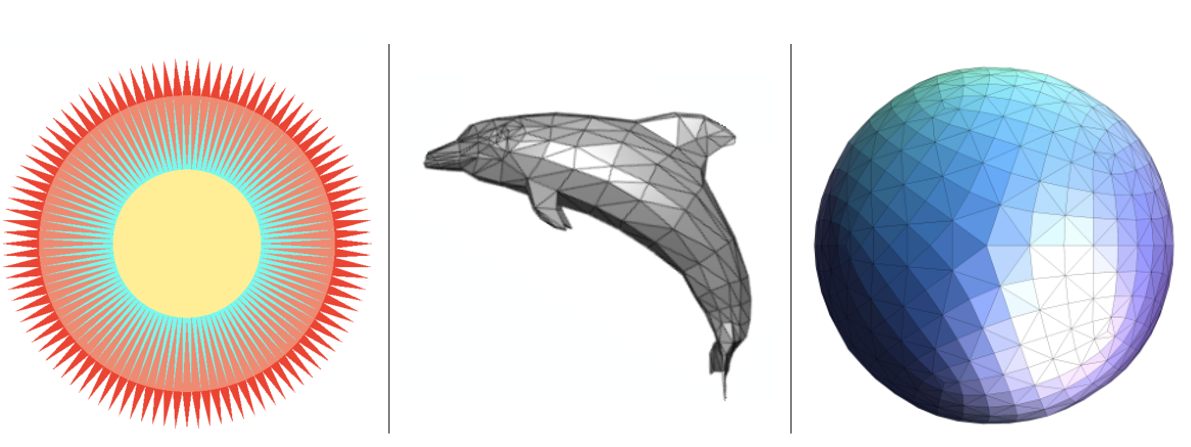
下圖中的老虎其實是由四邊形拼湊而成的

當然三角形其實也是可以作為fundamental shape primitives的。
三角形用的非常廣泛的,原因是因為它有如下幾個優秀特性:
- 三角形是最基本的多邊形
- 獨特性質
- Guaranteed to be planar (保證是平面的)
- well-defined interior(判斷一個點在不在三角形內非常方便)
- Well-defined method for interpolating values at
vertices over triangle (barycentric interpolation,重心插值)
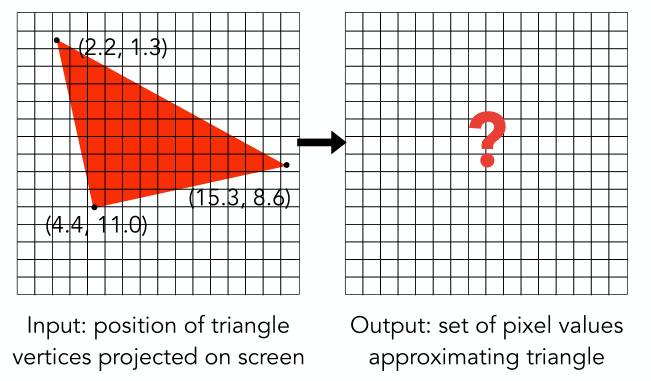
在經過MVP,以及將cuboid變換到屏幕空間(視口變換) 等一系列,假設我們得到了下圖左邊所示的三角形,三個頂點坐標已給出。
可以看到目前的頂點坐標還是小數,也就是說我們還需要將左邊的三角形轉化成像素表示形式。仔細觀察左邊的三角形你會發現三角形在某些像素格只占了很小的一部分,比如右邊的頂點,那么該頂點對應的像素到底是亮還是不亮呢? 下面就主要針對這個問題進行介紹,即判斷一個像素點和三角形的位置關系。
3.1 像素點位置關系判斷:采樣
判斷一個像素點和三角形的位置關系的一個比較簡單的辦法就是采樣(sampling)。
下面的代碼給出了采樣過程的示例,我們定義一個函數f(x),然后遍歷每個點,根據函數f(x)計算結果來判斷位置關系,即通過采樣來對函數進行離散化處理。 采樣在圖形學里應用的非常廣。
for (int x = 0; x < xmax; ++x){
for (int y = 0; y < ymax; ++y){
image[x][y] = inside(tri, x + 0.5, y + 0.5);
}
}
那上面的inside函數如何實現呢?這個其實在之前的筆記里有介紹,我們只需要通過叉乘即可知道點在三角形的內部還是外部。
以下圖(左)中的P點為例,我們分別計算
- \(\vec{CA}\times \vec{CP}\),計算得到的向量方向朝上;
- \(\vec{BC}\times \vec{CP}\),計算得到的向量方向也朝上;
- \(\vec{AB}\times \vec{CP}\),計算得到的向量方向也朝下。
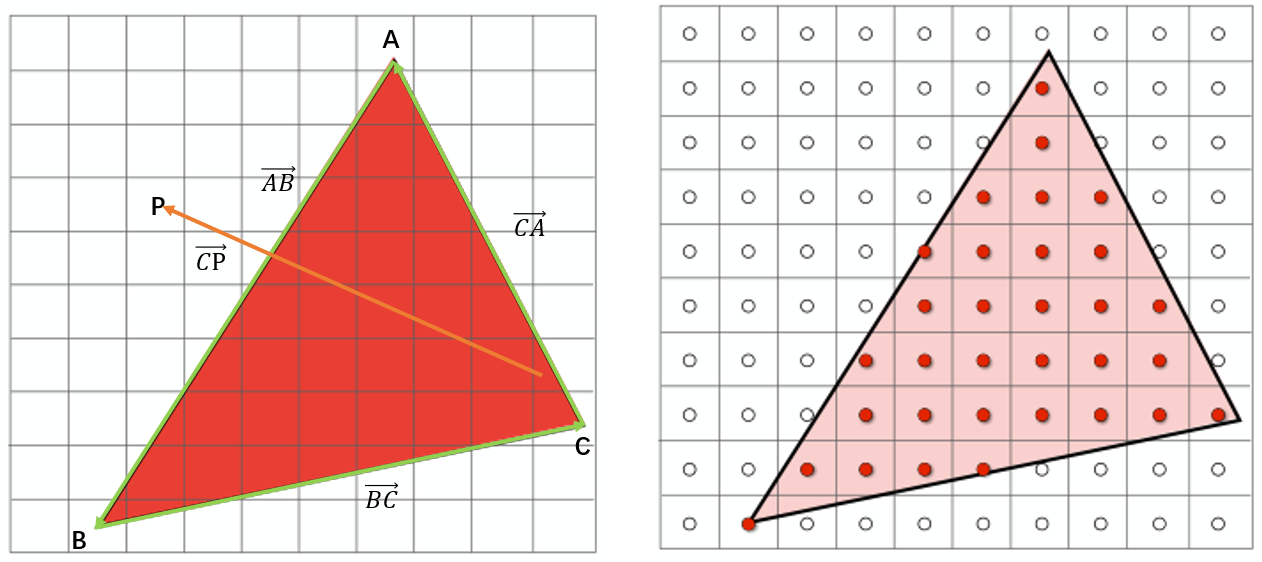
三條邊叉乘后的得到的向量方向不一致,所以可知\(P\)點在三角形外(注意\(P\)選取的是各個像素的中心點)。通過遍歷所有像素,即可知道下圖(右)中位於三角形的像素有哪一些了。最后得到的像素三角形如下:
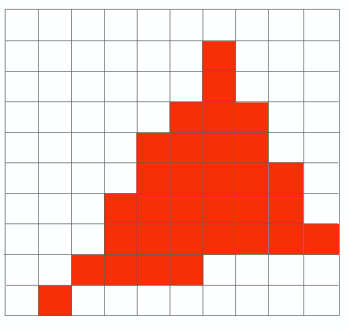
有的時候一個點可能是兩個三角形的頂點,那應該算那個三角形呢?這個沒有硬性要求,我們可以根據自己需要定義。
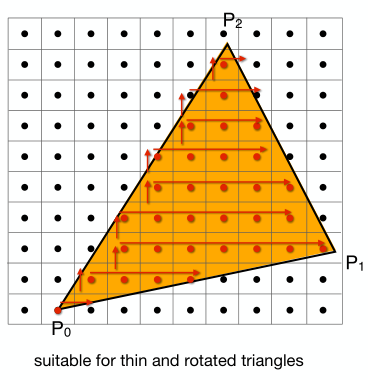
3.2 加速光柵化
另外對三角形的遍歷還有一些可以加速的操作:
-
根據頂點坐標確定bounding box,進而避免遍歷一些無必要的像素
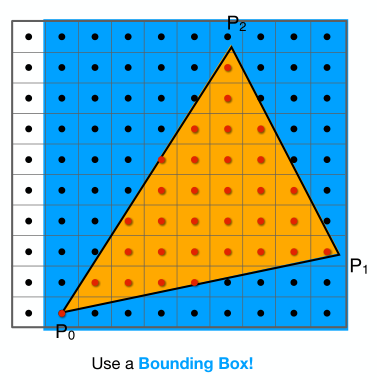
-
下圖給出了一個更極致的加速方法,遍歷起來一個額外像素點都沒有。但是這種方法實現起來復雜怡丟丟。