1. Why study transformation
1.1 Modeling
- translation (平移)
- rotation(旋轉)
- scaling (縮放)
- projection (投影)
2. 2D transformations: rotation, scale, shear
我們在求解變換矩陣的時候其實只需要去滿足一些特殊點即可算出變換矩陣了,而不需要死記硬背一些公式。具體可以看看旋轉矩陣的推導示例。
2.1 Scale (縮放變換)
假設原坐標為\(\left[\begin{array}{l}x \\ y\end{array}\right]\)
- Scale Matrix (縮放矩陣)
通過左乘一個Scale Matrix可以事先縮放變換,例如下式表示x,y坐標都縮放s倍。
- Reflection Matrix (反射矩陣)
Horizontal reflection
- Shear Matrix (剪切矩陣)
剪切變換(shear transformation)是空間線性變換之一,是仿射變換的一種原始變換。它指的是類似於四邊形不穩定性那種性質,方形變平行四邊形,任意一邊都可以被拉長的過程。
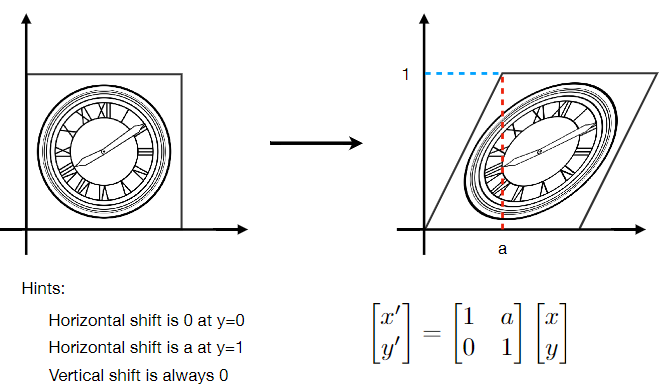
- Rotation Matrix (旋轉矩陣)
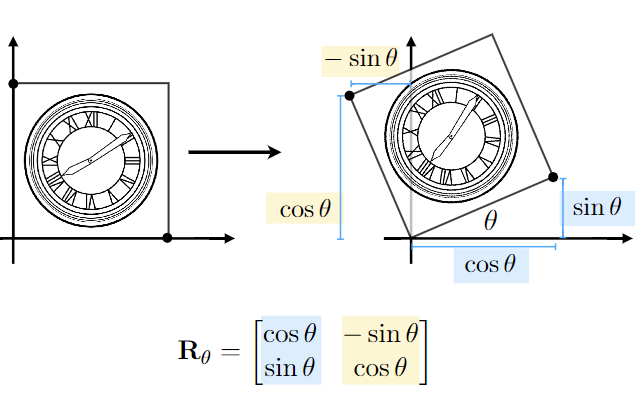
下面以右下角頂點為例進行旋轉矩陣計算,計算方法如下(其實就是求解方程組):
假設原坐標為(x,y),變換后的坐標為(x',y'),則有
為方便表示,假設為正方形邊長為1,那么可以得到如下等式
求解可得\(A=\cos \theta, C=\sin \theta\)
同理將左上角坐標變換代入計算即可求出B,D。
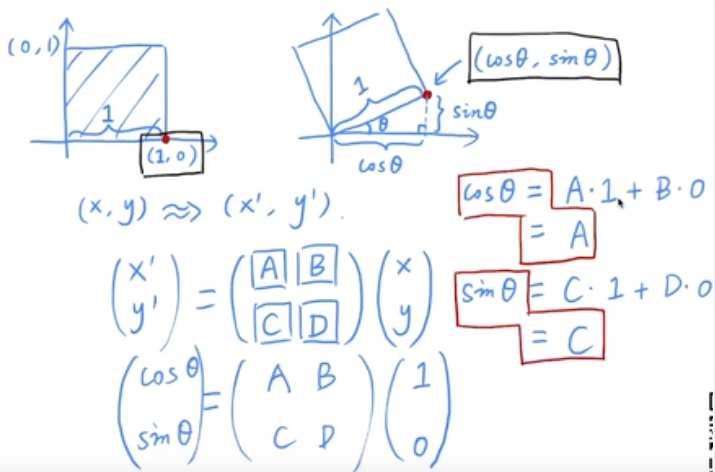
另外旋轉矩陣具有一些比較有意思的性質,這些性質在下一節會用到
- 旋轉θ角度
\(R_{\theta}=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right)\) - 旋轉-θ角度
\(R_{-\theta}=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{array}\right)\)
很顯然有\(R_{-\theta}=R_\theta^T\),而又由定義可知\(R_{-\theta}=R_\theta^{-1}\),因為這兩個操作是互逆的嘛。
也就是說\(R_{-\theta}=R_\theta^T=R_\theta^{-1}\),而在數學上如果一個矩陣的逆等於它的轉置,那么就稱這個矩陣為正交矩陣(Orthogonal Matrix),即旋轉矩陣是正交矩陣。
3. Homogeneous coordinates (齊次坐標)
3.1 為什么需要引入齊次坐標呢?
首先看一下平移操作
轉化成矩陣形式如下:
顯然上述操作並不能用矩陣乘法來表示,因此平移變換不能像前面的變換操作一樣可以直接用矩陣乘法表示,所以為了讓平移變換也可以以一種優雅的矩陣乘法形式表示,所以需要引入齊次坐標。
3.2 如何使用齊次坐標
以二維坐標為例,我們可以通過額外加入一個坐標來使用齊次坐標。因此:
- 一個2D的點,可以表示為\((x, y, 1)^{\top}\)
- 一個2D向量,可以表示為\((x, y, 0)^{\top}\)
3D情況同理,表示如下:
- 3D point \(=(x, y, z, 1)^{\top}\)
- 3D vector \(=(x, y, z, 0)^{\top}\)
那為什么點和向量最后一項一個是1,而另一個是0呢?仔細想想這樣設計是非常smart的操作,因為它滿足了如下性質:
- vector + vector = vector (第三維仍然是0,所以表示向量)
- point - point = vector (這符合我們學習向量時所給出的定義,即某點指向另一個點,那不就表示向量了嗎,而且相減之后第三維恰巧就是0)
- point + vector = point (這個很好理解,不再贅述)
- point + point = ?point
最后一個我們用一個例子來說明,假設兩個點分別為\(a=(0, 1, 1)^{\top},b=(0, 3, 1)^{\top}\),那么\(c=a+b=(0, 4, 2)^{\top}\),因為第三維只能是0或者1,所以我們可以對每一維除以2,那么就可以得到\(c=(0, 2, 1)^{\top}\),這不就是a,b的中點嗎!!!是不是感覺很奇妙!
3.3 Affine Transformations (仿射變換)
為了將上述變換統一起來,所以提出了仿射變換,即
Affine map = linear map + translation
(仿射變換 = 線性變換 + 平移變換)
用齊次坐標可以將仿射變換計算公式表示如下:
2D的線性變化在齊次坐標下的表示形式總結如下:
Scale,Rotation,Translation分別表示如下
4. Composing transforms
上述變換可以組合起來實現各種各樣的效果,但是需要注意的是各個變換的順序是非常重要的,因為矩陣乘法不滿足交換律。
因為本課程默認向量表示形式為列向量,所以矩陣變換應該是對向量做成矩陣,比如先對向量旋轉45°,然后沿X軸平移一個單位,則可以表示如下:
注意:\(R_{45} \cdot T_{(1,0)} \neq T_{(1,0)} \cdot R_{45}\)
推廣開來,若干個變換可以表示如下:
仔細觀察可以知道左邊一系列的矩陣相乘其實就等價於一個3x3的矩陣,換句話說一個3x3矩陣可以對2D向量做超級多的變換。
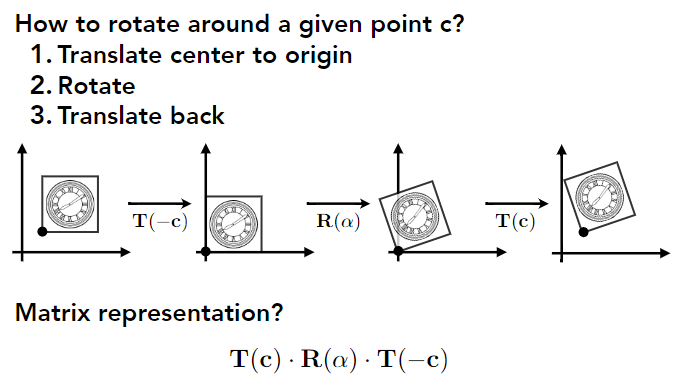
如果一個變化比較復雜該怎么弄呢?很簡單我們可以通過對復雜變化做分解來簡化,例如如果我們想以下圖中(最左邊)的正方形左下角為中心進行旋轉該怎么做呢?
很簡單我們可以先將左下角頂點通過平移變換移動到原點,然后再做旋轉,最后將左下角頂點平移回原處即可。