1. 回顧和本節摘要
1.1 上一節內容回顧
- Viewing
- View + Projection + Viewport(將cuboid變換到屏幕空間)
- Rasterizing triangles
- Point-in-triangle test
- Aliasing:像素引起的鋸齒狀失真。
1.2 本節內容概要:
- Antialiasing
- Sampling theory
- Antialiasing in practice
- Visibility / occlusion
- Z-buffering
下圖給出了Alias(圖像失真)的例子。最左邊是計算出的在三角形內的像素中心點,中間是我們想要得到的效果,右邊是實際效果。買家秀和賣家秀。。。這個現象的學名就叫aliasing。下面主要介紹如何防止失真走樣。

2. Sampling Artifacts (SA)
在圖形學里,artifacts指的是Errors / Mistakes / Inaccuracies,泛指一些不准確或者與我們預期不一樣的結果。
SA有如下幾類:
- Jaggies – sampling in space
- Moire – undersampling images
- Wagon wheel effect – sampling in time
- [Many more] …
主要原因是因為信號變化太快,而采樣太慢。
一種反走樣(Antialiasing)的方法是對原圖先做模糊處理(濾波),然后再采樣。效果可以看下面幾個示例
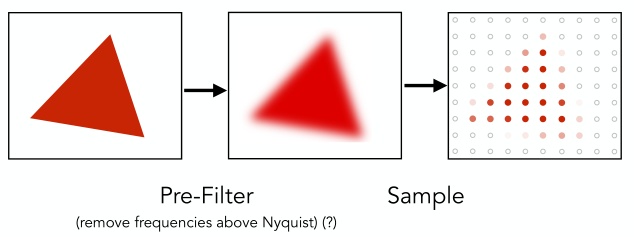

但是如果我們先采樣,然后再濾波,效果如下圖左邊,可以看到效果並不好。為什么采樣和濾波的順序這么重要呢?下面從頻域角度對這一現象進行介紹和分析。
3. Frequency Domain (頻域)
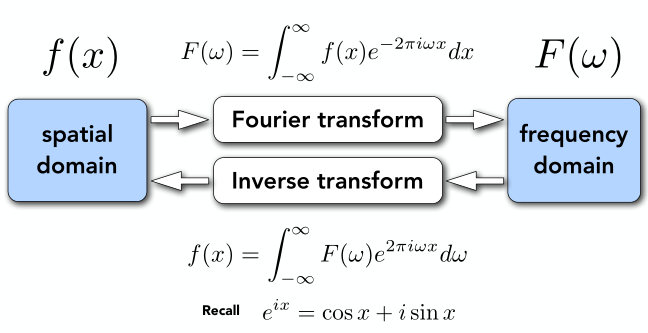
3.1 傅里葉級數
傅里葉級數能將任何周期函數或周期信號分解成一個(可能由無窮個元素組成的)簡單振盪函數的集合,即正弦函數和余弦函數(或者,等價地使用復指數)。
傅里葉級數展開示例:
3.2 走樣
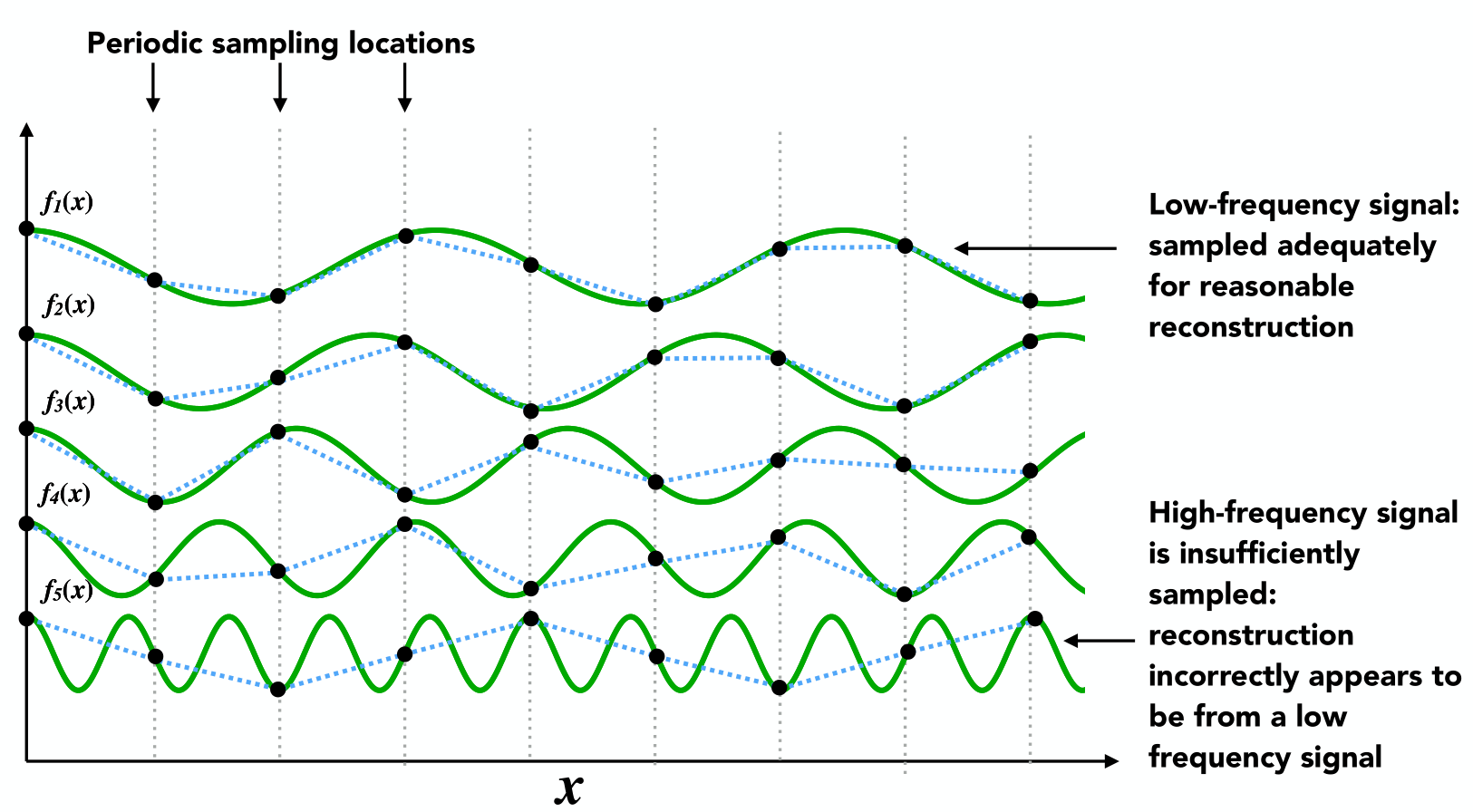
前面提到走樣的原因是信號變化太快,而采樣太慢。觀看這句話可能不太能理解,但是結合下面的圖應該就很好理解了。
可以看到有五條不同的綠色曲線,分別表示不同的信號。黑色的點表示每隔一段時間對信號采樣得到的點。可以看到對於\(f_1(x)\),因為他的頻率較慢,所以我們通過連接采樣得到的黑點其實大致上還是能還原出原信號的。而隨着信號頻率不斷增加,以\(f_5(x)\)為例,此時很顯然我們無法還原信號了。
3.3 Filtering(濾波)
濾波表示去除某種特定的頻率(如高頻、低頻)信息。
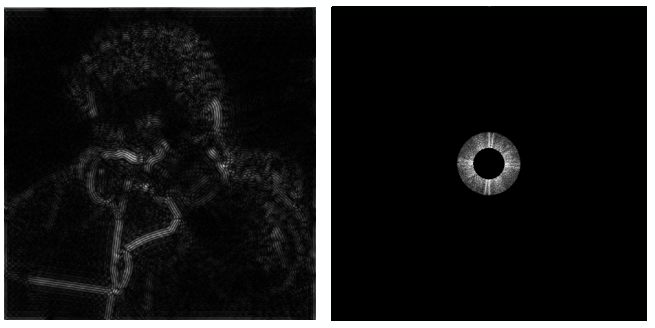
下圖是原圖:

- high-pass filter 高通濾波
下圖展示了高通濾波的效果。高通即只有高頻信息留下,而濾掉低頻信息。那什么是高、低頻信息呢?
簡單理解就是顏色變化劇烈的就是高頻信息,比如上面右圖中心基本上都是白色的,這就是低頻信息,所以使用高通濾波后中間的光亮就被去掉了。同理,對於左圖而言,高頻信息指的就是那些邊界,因為邊界的顏色或者光亮變化更強烈,可以看到最后剩下的是人的輪廓。

- low-pass filter 低通濾波

- band-pass filter 帶通濾波
3.4 卷積(convolution)
通過上面的分析可以知道一張圖可以看作是由低頻、高頻、和其他頻段的信號組成的。如果我們想要得到高頻信號,那么就等價於給高頻信號權重為1,其他頻段信號權重為0。換言之,濾波其實就是加權求和,也就是卷積,即
Filtering = Convolution = Average
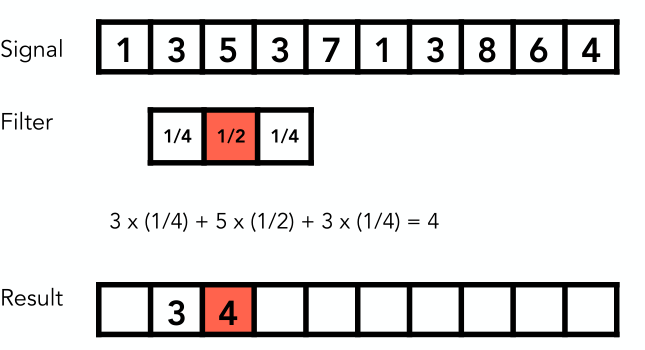
卷積定理
時域(spatial domain)上的卷積等價於頻域(frequency domain)上的乘積;
時域上的乘積等價於頻域上的卷積;
比如我對一張圖片做卷積操作,等價於我們先把圖片和卷積核通過傅里葉變換轉化到頻域上,然后在頻域上將兩者相乘(可以理解成乘了一個mask),最后將相乘的結果做逆傅里葉變換即可。
現在我們思考這么一件事情:時域上卷積核的大小和頻域上是什么關系? 比如是正相關還是負相關?
答案是負相關。為了方便理解,我們舉幾個極端的情況。
假設在時域上,卷積核大小是整張圖的大小,那么簡單理解就是把圖片上所有像素的值做平均,這樣得到的值肯定和原來像素值差別很大,最后得到的圖片應該是非常模糊的,換句話說圖片里很多信息都丟掉了。而前面說了,時域上的卷積等價於頻域上的乘積,而這個乘積進一步可以簡單理解成就是乘了一個mask,因為圖片信息丟掉了很多,那不就代表這個mask的非零值很少嗎。總結來說就時域上卷積核越大,那么對應地頻域上的卷積核就越小。
(下面給出了兩種情況的卷積核示意圖,可以看到左邊的卷積核小一些,對應到頻域上大一些。)

3.5 采樣(sampling)
采樣等價於重復頻率信息。
Sampling = Repeating Frequency Contents
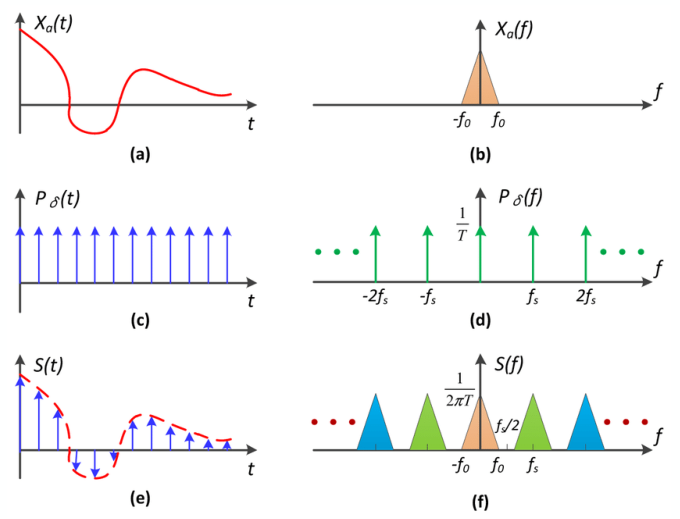
下圖左側(a,c,e)表示時域上的操作,右側(b,d,f)表示頻域上的操作。其中(a)表示時域信號,(b)表示信號在頻域上的樣子(這里畫成三角形是為了好理解,什么樣子其實無所謂,不影響理解)。
(c)表示沖激采樣,即每隔一段時間就采樣一次,它在頻率上的其實也和沖激信號長得一樣(d)。
在時域上的采樣(e)其實就是信號和沖激采樣相乘\(x_a(t)\times p_\delta(t)\),那么對應到頻域就是二者做卷積(f)。
得到的效果可以看到在頻域上其實就是對原頻域信號不斷的重復。
當然上面給出的是一種比較理想的情況,如果采樣間隔較長(或者說采樣較慢)的話則會導致下面sparse sampling的情況,即頻域信號之間在重復時發生了混疊,及導致了aliasing現象。
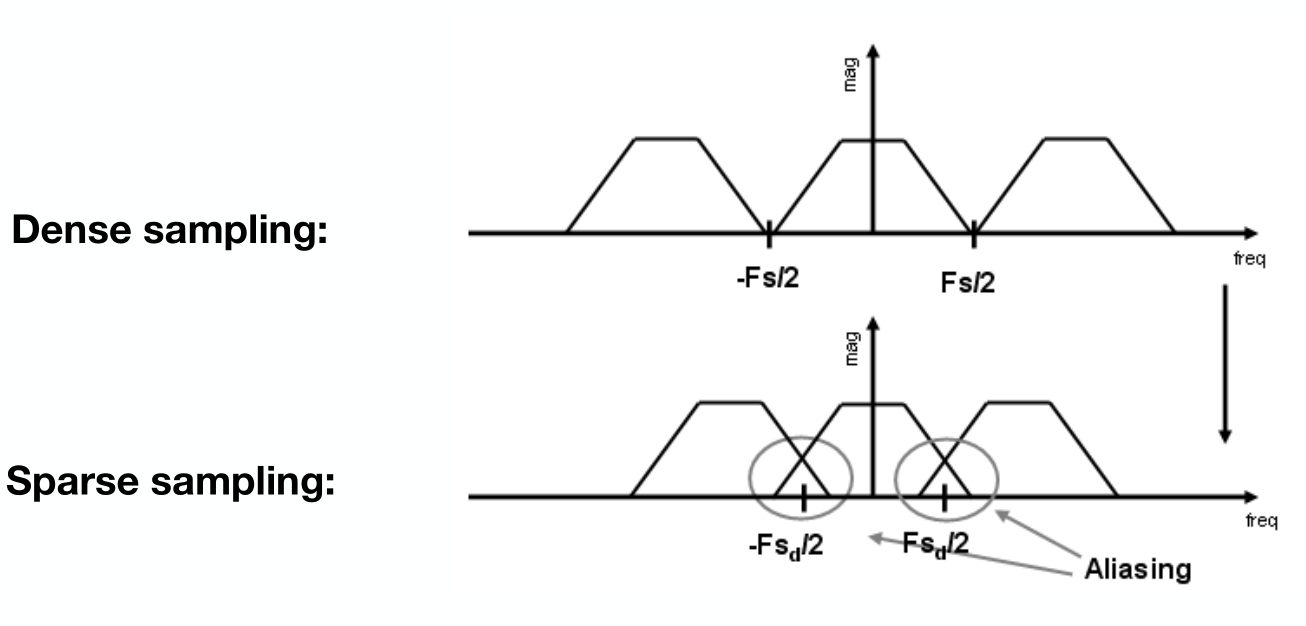
(注意:上圖表示的是頻域上的信號表示,橫軸表示頻率,縱軸表示幅度,即信號強度)
3.6 反走樣(Antialiasing)
上面介紹了走樣發生的原因,那么如何反走樣呢?
一種本質的方法是提高采樣速率。但是很多情況下這不現實,我總不能隨便改變一個手機或者電視的刷新頻率吧?
那么另外一種替代的方法就是我對信號做截斷處理,如下圖示。可以看到通過截斷高頻信號(注意橫軸表示頻率),這樣我們就可以避免了走樣現象發生,即實現了反走樣。
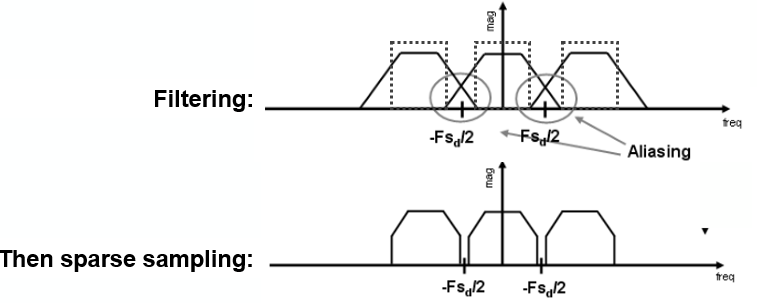
到此為止,也就解釋了我們最前面給的例子,即先對三角形做濾波(模糊操作),然后再采樣。

那么對三角形模糊處理具體是怎么做的呢?其實就是在頻域上使用低通濾波將器乘以這個三角形的頻域信號即可,也就是模糊操作(高通濾波的效果是保留輪廓),那對應到時域上我們可以使用一個像素大小的卷積核對單個像素做卷積操作,什么意思呢?
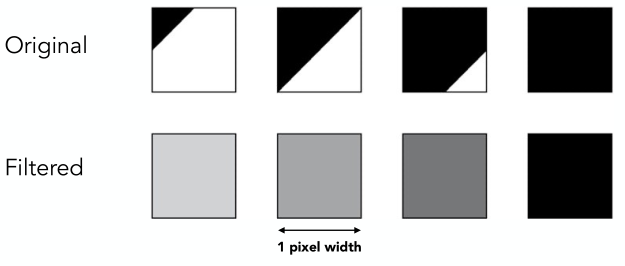
下圖給出了單個像素內被三角形覆蓋面積的不同情況:
以最左邊的像素為例,黑色表示三角形覆蓋的面積,可以看到大約是覆蓋了1/8的面積,那么做平均之后這個像素對應的亮度值就是純白色的7/8。
4. Antialiasing By Supersampling (MSAA)
上面對每個像素內部做平均計算不太好計算,所以一種改進的算法MSAA誕生了。
MSAA的大致思路是從邏輯上把一個像素點再細分,比如把一個像素點划分成4個child-points (a→b)。
然后通過child-point覆蓋的數量來計算對應的顏色(c,d)
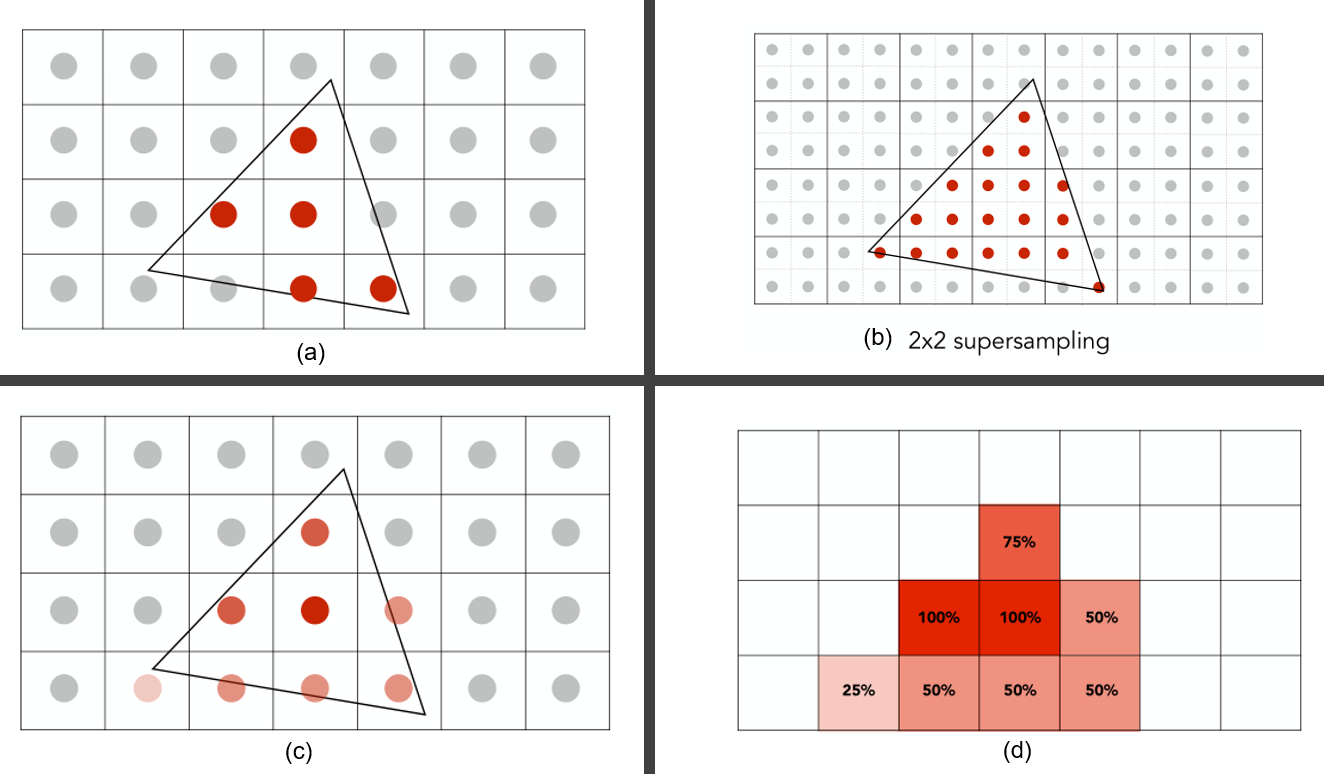
但是MSAA一個很明顯的缺點就是計算量增加了4倍。。。
后續又不好改進算法,這里不做詳細介紹了:
- FXAA (Fast Approximate AA)
- TAA (Temporal AA)
