概念
- 歐拉路徑:圖&G&中的一條路徑若包括每個邊恰好一次,則其為歐拉路徑
- 歐拉回路:一條回路如果是歐拉路徑,那么其為歐拉回路
存在條件
無論無向圖還是有向圖,首要條件為所有邊都是連通的
- 無向圖
- 存在歐拉路徑的充要條件:度數為奇數的點只能有0或2個
- 存在歐拉回路的充要條件:度數為奇數的點只能有0個
- 有向圖
- 存在歐拉路徑的充要條件:所有點出度=入度;或除兩點外其余所有點出度=入度,余下兩點一個出度-入度=1(地點),另一個入度-出度=1(終點)
- 存在歐拉回路的充要條件:所有點出度=入度
注:歐拉回路為歐拉路徑的一種特例,因此如果說存在歐拉路徑是包含存在歐拉回路這種情況的
算法流程
1. 建圖並統計點的度數(有向圖分入度和出度)
2. 根據度數進行初步的有解性判定
如何理解"初步":所有點的度數均滿足要求不等價於所有邊均連通。連通性判定在此處無法解決,因此為初步的合法性判定
-
無向圖
統計度數為奇數的點個數count- 歐拉回路:
count == 0 - 歐拉路徑:
count == 0 || count == 2
- 歐拉回路:
-
有向圖
- 歐拉回路:有解僅需保證所有點入度==出度即可
- 歐拉路徑:
設din[i]為i點的入度,dout[i]為i點的出度
dout[i] - din[i] == 1的點數為startNum(滿足起點特征)
din[i] - dout[i] == 1的點數為endNum(滿足終點特征)
success表示是否有解
方法1:
for (int i = 1; i <= n; ++i) // 枚舉所有點 if (din[i] != dout[i]) { if (dout[i] - din[i] == 1) ++ startNum; else if (din[i] - dout[i] == 1) ++endNum; else success = false; }有解的條件為
success && (!startNum && !endNum || startNum == 1 && endNum == 1)
比較容易理解的是success為false時一定是無解的
不容易理解的是,success為true時不一定是有解的,因為最多只能有2個點的出度!=入度,而success為true並不能保證這一點方法2:
設count為出度!=入度的點個數,flag為出度!=入度點的(出度-入度)的乘積(或者入度-出度的乘積)for (int i = 1; i <= n; ++i) // 枚舉所有點 if (din[i] != dout[i]) { ++count; flag *= dout[i] - din[i]; }有解的條件為
!count || (count == 2 && flag == -1)
即出度!=入度的點數為0 或 出度 != 入度的點數為2並且對應兩個點,起點滿足dout[i] - din[i] == 1, 終點滿足dout[i] - din[i] == -1
注:如果題目保證至少存在一組解,則此判定過程可以省略
3. 選取起點
首先需要明確兩點
- 從歐拉回路上任意一點
dfs均可搜索到其所在的歐拉回路- 從歐拉路徑上任意一點
dfs未必可以搜索到其所有的歐拉路徑,必須從滿足一定性質的點出發才可
原因很簡單,對於一個環路來說,從任意一點開始都可以一筆畫出整個環;對於一個路徑,只有從起點開始才可以一筆畫出整條路徑
- 歐拉回路:如果題目要求的為歐拉回路,在無向圖中,滿足所有點的度數為偶數,在有向圖中,滿足所有點的出度==入度,所有點都是等價的,因此
dfs的起點只需定為一個非孤立點
為何一定是非孤立點: 在此類題目中,一般不能保證點是連通的,因此是存在孤立點的,但是孤立點的存在對歐拉回路或路徑的存在並不產生影響,但是如果從孤立點開始是找不到回路或路徑的
- 歐拉路徑:如果題目要求的為歐拉路徑,對於無向圖,需要找到度數為奇數的點作為起點,對於有向圖,需要找到
dout[i] - din[i] == 1的點\(i\)
4.從起點開始dfs尋找歐拉回路或歐拉路徑
歐拉回路和歐拉路徑問題的本質是邊的問題,類比對點的dfs問題,我們同樣需要對走過的邊進行標記,防止重復
void dfs(int u)
{
for (int i = h[u]; ~i; i = ne[i])
{
if (st[i]) continue; // 對走過的邊進行標記
st[i] = true;
dfs(e[i]);
res[++cnt] = i;
}
}
dfs部分難點-遞歸搜索和存儲答案的順序問題
dfs(e[i]);
res[++cnt] = i;
在常規dfs中,搜索到某個點會首先把該點進行存儲,然后再遞歸搜索,但是求解歐拉路徑需要遞歸搜索完一個節點后再把到該節點的邊進行存儲
為了說明這兩種順序產生的不同結果,以一組數據為例
/**
* 無向圖
* 5個點,6條邊
* 以下6行a b表示:a與b之間有一條邊
*/
5 6
2 3
2 5
3 4
1 2
4 2
5 1
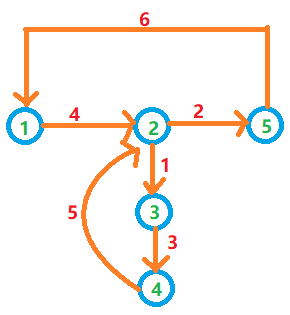
對邊進行存儲,
- 如果采取先存儲再搜索的順序,結果為
4 2 6 1 3 5 - 如果采取先搜索再存儲的順序,結果為
6 2 5 3 1 4
可以發現,第二種順序得到的恰好是歐拉路徑的倒序,結果只需要倒序輸出即可
dfs部分難點-優化問題
最終的優化方案實際分為兩個部分,為了更加透徹理解優化原理,逐層進行分析
- 原始思路
void dfs(int u)
{
for (int i = h[u]; ~i; i = ne[i])
{
if (st[i]) continue; // 對走過的邊進行標記
st[i] = true;
// 如果為無向圖,這里還需要對反向邊進行標記
dfs(e[i]);
res[++cnt] = i;
}
}
上述代碼為一般思路,存在的問題為走過的邊存在重復枚舉。添加了st[]用於對邊進行判重,只能保證不去走已經走過的邊,但是不能保證不去枚舉已經走過的邊。
考慮下面的情況,對於\(1\)號點,第一步走到\(2\)號點,則\(1->2\)的邊被搜索過了,但從\(2->5->1\)又一次走到\(1\)號點時,for循環還會枚舉一次\(1->2\)這條邊,st的存在使得不會去走這條邊,但是仍會枚舉這條邊
只要這條邊沒有被刪除,那么只要到達\(1\)號點,\(1->2\)這條邊就會被枚舉一次,顯然這是一次無效的枚舉,當無效枚舉次數過多時就會TLE
/**
* 無向圖
* 5個點,6條邊
* 以下6行a b表示:a與b之間有一條邊
*/
5 6
2 3
2 5
3 4
1 2
4 2
5 1

- 第一次優化
上述分析提到,“只要一條已經走過的邊沒有被刪除,那么就有可能發生無效枚舉”,因此優化方案為刪除已經走過的邊
在鏈式結構中,如果不采用雙向鏈表無法在\(O(1)\)的時間內刪除某點,而以現有的存儲結構是無法做到這一點的同時改變存儲結構相對復雜,因此采取如下方案
對於隊首指針(h[u])指向的第一條邊\(i\)
- 如果其已經被搜索過(
st[i] == true),那么直接刪除,因為是第一條邊,因此可以通過直接修改隊首指針(h[u] = ne[i])實現,然后繼續枚舉下一條邊 - 如果其沒有被搜索過(
st[i] == false),那么刪除這條邊,並標記該邊走過,然后對該邊的后續節點進行枚舉
for (int i = h[u]; ~i; i = ne[i])
{
if (st[i])
{
h[u] = ne[i];
continue;
}
h[u] = ne[i];
s[i] = true;
// 無向圖還需要對反向邊進行標記
dfs(e[i]);
res[++cnt] = i;
}
注:第2種方案中,既然已經將邊刪除,為何還需要進行標記?
答:這里不標記也是對的,因為該邊起點的隊首指針已經被修改,因此不會再搜索到這條邊,因此不標記對答案也不會產生影響。
但是在無向圖中,我們能刪除的僅是當前這個方向,而不能修改反方向。我們雖然可以獲取到反方向邊的編號,但是通過修改h數組來實現刪邊的前提是當前邊為隊首指針指向的第一條邊,而我們無法保證當前邊的終點的隊首指針指向的是當前邊的反向邊,因此無向圖中方向邊必須進行標記而非刪除,既然有些邊實際被走過只進行了標記但卻沒有刪除,因此if(st[i])的判斷也是不可以省略的
按照注中分析,將邊刪除后可以不進行標記,即下方代碼,但顯然這樣做並沒有大幅度減少代碼量反倒增加了思維量,因此一般情況下會選擇既標記又刪除
for (int i = h[u]; ~i; i = ne[i])
{
if (st[i])
{
h[u] = ne[i];
continue;
}
h[u] = ne[i];
// 無向圖還需要對反向邊進行標記
dfs(e[i]);
res[++cnt] = i;
}
- 第2次優化
第1次優化后的代碼仍然存在的問題是,我們僅僅通過修改h[]實現了刪邊,但是ne[]的信息並沒有同步發生變化。
由於代碼采取的遞歸加回溯的實現方式,因此可能發生的情況是遞歸過程中一些邊被刪除了,但當回溯時,由於ne[]的信息沒有改變,所有仍有可能搜索到這些邊,這些無效搜索仍可能造成TLE
一個典型的例子為,圖中僅一個點,很多條自環,考慮第一層dfs所有第一條邊,其下的所有層遞歸會將所有邊刪除,但是回到第一層時i = ne[i]會繼續搜索它的下一條邊
解決方法為讓每次的i都從隊首指針指向的第一條邊開始搜索(h[u]),因為我們的搜索策略保證了h[u]始終為第一條未搜索過的邊,因此可以從h[u]開始從而消除因ne[]與h[]信息不同步帶來的影響
for (int i = h[u]; ~i; i = h[u])
{
if (st[i])
{
h[u] = ne[i];
continue;
}
h[u] = ne[i];
st[i] = true;
// 無向圖還需要對反向邊進行標記
dfs(e[i]);
res[++cnt] = i;
}
5. 根據dfs結果進行終極判定
dfs后得到一個答案序列,此時需要判斷序列中邊的條數與總邊數的關系,因為分析到這里我們仍然沒有確定所有邊是否均連通,因此獲得的序列並不一定是合法的
只有在各點滿足了度數的要求,並且判定出所有邊均連通的條件下,才可以判定出歐拉回路或歐拉路徑是存在的
- 如果答案序列中邊的數目等於總邊數,說明所有邊是連通的,且成功找到了歐拉回路或歐拉路徑
- 如果答案序列中邊的數目小於總邊數,說明不滿足所有邊連通的條件,即不存在歐拉回路或路徑
例題
雖然在算法流程的討論中,對歐拉回路和歐拉路徑分開進行了討論,但是由於歐拉回路是歐拉路徑的一種特例,因此用歐拉路徑的更具普適性的代碼是可以解決歐拉回路的問題的,
只不過如果題目明確告知了是求歐拉回路,那么起點的的選取過程可以更簡單,代碼量更少一些
無向圖求歐拉路徑
題目描述

解題思路
本題核心為無向圖求歐拉路徑,但題目有兩點特殊之處:
- 題目保證至少一個解。這保證了我們不需要根據度數進行初步的有解性判定,而且在選定起點
dfs之后也不需要比較答案序列中的邊數和總邊數的關系進行最終有解性判定 - 題目要求輸出字典序最小的答案序列,只需保證優先搜索序號較小的點即可實現這一點,若采用鄰接表存儲在建圖后還需要進行排序,同時會牽扯出很多問題,而采用鄰接矩陣則可以不需要額外操作輕松實現這一點要求
代碼實現
#include <iostream>
using namespace std;
const int N = 510, M = 1100;
int n, m;
int g[N][N];
int res[M], cnt;
int d[N];
void dfs(int u)
{
for (int i = 1; i <= n; ++i)
if (g[u][i]) {
--g[u][i], --g[i][u];
dfs(i);
}
res[++cnt] = u;
}
int main()
{
cin >> m;
for (int i = 0; i < m; ++i) {
int x, y;
cin >> x >> y;
++g[x][y], ++g[y][x];
++d[x], ++d[y];
n = max(n, max(x, y));
}
/**
* 這里不采用嘗試性dfs的原因是,每次dfs都會對g數組進行修改,如果本次dfs沒有得出結果還需要恢復原樣,較為復雜,因此還是通過歐拉路徑的性質找到合法的起點開始dfs
* 所謂嘗試性dfs是指,不管通過本次dfs的點能夠找到歐拉路徑,都選擇從這一點開始dfs試一試,如果不能那么再嘗試dfs其它點
*/
// for (int i = 1; i <= n; ++i)
// if (!d[i]) {
// dfs(i);
// if (cnt == m + 1) break;
// cnt = 0;
// // 后續需要恢復dfs前的原樣,恢復二維數組的過程比較浪費時間
// }
/**
* 為什么可以提前確定起點
* 首先合法的起點一定是非孤立點,即度數不能為0,可以保證孤立點一定不是起點
* 其次,如果存在度數為奇數的點,如果該點不作為起點,那么一定無法找到歐拉路徑,所以只能將該點作為起點
*/
int start = 1;
while (!d[start]) ++start;
for (int i = 1; i <= n; ++i)
if (d[i] % 2) {
start = i;
break;
}
dfs(start);
for (int i = cnt; i; --i) cout << res[i] << endl;
return 0;
}
有向圖求歐拉路徑
題目描述

解題思路
本題的建圖方式其實算是第一個難點,如果選取單詞為點,兩個單詞是否存在可連接的關系為邊,那么題目實際為一哈密頓路徑問題
如果選取單詞的首尾字母為點,每個單詞為邊,那么題目就會轉化為有向圖的歐拉路徑問題
完成問題的轉化之后,按照上述4個步驟進行求解即可
代碼實現
有向圖求歐拉路徑在由度數初步判定合法性時,提出了兩種方法,這里分別實現一下
// 方法1
#include <iostream>
#include <cstring>
using namespace std;
const int N = 30, M = 1e5 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int din[N], dout[N];
bool st[M];
int res[M], cnt;
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u)
{
for (int i = h[u]; ~i; i = h[u])
{
if (st[i])
{
h[u] = ne[i];
continue;
}
h[u] = ne[i];
st[i] = true;
dfs(e[i]);
res[++cnt] = i;
}
}
int main()
{
int T;
cin >> T;
while (T --)
{
cin >> m;
n = 0;
idx = cnt = 0;
memset(din, 0, sizeof din);
memset(dout, 0, sizeof dout);
memset(st, 0, sizeof st);
memset(h, -1, sizeof h);
for (int i = 0; i < m; ++i)
{
string str;
cin >> str;
int a = str[0] - 'a', b = str[str.size() - 1] - 'a';
add(a, b);
++dout[a], ++din[b];
n = max(n, max(a, b));
}
bool success = true;
int count = 0, flag = 1, start = 0, startNum = 0, endNum = 0;
while (!din[start] && !dout[start]) ++start;
for (int i = 0; i <= n; ++i)
if (din[i] != dout[i])
{
if (dout[i] - din[i] == 1)
{
start = i;
++startNum;
}
else if (din[i] - dout[i] == 1) ++endNum;
else
{
success = false;
break;
}
}
if (success && (!startNum && !endNum || startNum == 1 && endNum == 1))
{
dfs(start);
if (cnt == m) cout << "Ordering is possible." << endl;
else cout << "The door cannot be opened." << endl;
}
else cout << "The door cannot be opened." << endl;
}
return 0;
}
// 方法2
#include <iostream>
#include <cstring>
using namespace std;
const int N = 30, M = 1e5 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int din[N], dout[N];
bool st[M];
int res[M], cnt;
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void dfs(int u)
{
for (int i = h[u]; ~i; i = h[u])
{
if (st[i])
{
h[u] = ne[i];
continue;
}
h[u] = ne[i];
st[i] = true;
dfs(e[i]);
res[++cnt] = i;
}
}
int main()
{
int T;
cin >> T;
while (T --)
{
cin >> m;
idx = cnt = 0;
memset(din, 0, sizeof din);
memset(dout, 0, sizeof dout);
memset(st, 0, sizeof st);
memset(h, -1, sizeof h);
for (int i = 0; i < m; ++i)
{
string str;
cin >> str;
int a = str[0] - 'a', b = str[str.size() - 1] - 'a';
add(a, b);
++dout[a], ++din[b];
n = max(n, max(a, b));
}
int count = 0, flag = 1, start = 0;
while (!din[start] && !dout[start]) ++start;
for (int i = 0; i <= n; ++i)
if (din[i] != dout[i])
{
++count;
flag *= dout[i] - din[i];
if (dout[i] - din[i] == 1) start = i;
}
if (!count || (count == 2 && flag == -1))
{
dfs(start);
if (cnt == m) cout << "Ordering is possible." << endl;
else cout << "The door cannot be opened." << endl;
}
else
cout << "The door cannot be opened." << endl;
}
return 0;
}
