碼上快樂

相關內容    簡體    繁體

NetworkX系列教程(9)-線性代數相關

本文轉載自   查看原文   2018-06-20 21:47   1865 
小書匠  Graph  圖論 

學過線性代數的都了解矩陣,在矩陣上的文章可做的很多,什么特征矩陣,單位矩陣等.grpah存儲可以使用矩陣,比如graph的鄰接矩陣,權重矩陣等,這節主要是在等到graph后,如何快速得到這些信息.詳細官方文檔在這里

目錄:

注意:如果代碼出現找不庫,請返回第一個教程,把庫文件導入.

10線性代數相關

10.1圖矩陣

  1. #定義圖的節點和邊 
  2. nodes=['0','1','2','3','4','5','a','b','c'] 
  3. edges=[('0','0',1),('0','1',1),('0','5',1),('0','5',2),('1','2',3),('1','4',5),('2','1',7),('2','4',6),('a','b',0.5),('b','c',0.5),('c','a',0.5)] 
  4.  
  5. plt.subplots(1,2,figsize=(10,3)) 
  6.  
  7. #定義一個無向圖和有向圖 
  8. G1 = nx.Graph() 
  9. G1.add_nodes_from(nodes) 
  10. G1.add_weighted_edges_from(edges) 
  11.  
  12. G2 = nx.DiGraph() 
  13. G2.add_nodes_from(nodes) 
  14. G2.add_weighted_edges_from(edges) 
  15.  
  16. pos1=nx.circular_layout(G1) 
  17. pos2=nx.circular_layout(G2) 
  18.  
  19. #畫出無向圖和有向圖 
  20. plt.subplot(121) 
  21. nx.draw(G1,pos1, with_labels=True, font_weight='bold') 
  22. plt.title('無向圖',fontproperties=myfont) 
  23. plt.axis('on') 
  24. plt.xticks([]) 
  25. plt.yticks([]) 
  26.  
  27. plt.subplot(122) 
  28. nx.draw(G2,pos2, with_labels=True, font_weight='bold') 
  29. plt.title('有向圖',fontproperties=myfont) 
  30. plt.axis('on') 
  31. plt.xticks([]) 
  32. plt.yticks([]) 
  33.  
  34. plt.show() 
  35.  
  36. #控制numpy輸出小數位數 
  37. import numpy as np 
  38. np.set_printoptions(precision=3)  
  39.  
  40. #鄰接矩陣 
  41. A = nx.adjacency_matrix(G1) 
  42. print('鄰接矩陣:\n',A.todense()) 
  43.  
  44. #關聯矩陣 
  45. I = nx.incidence_matrix(G1) 
  46. print('\n關聯矩陣:\n',I.todense()) 
  47.  
  48. #拉普拉斯矩陣 
  49. L=nx.laplacian_matrix(G1) 
  50. print('\n拉普拉斯矩陣:\n',L.todense()) 
  51.  
  52. #標准化的拉普拉斯矩陣 
  53. NL=nx.normalized_laplacian_matrix(G1) 
  54. print('\n標准化的拉普拉斯矩陣:\n',NL.todense()) 
  55.  
  56. #有向圖拉普拉斯矩陣 
  57. DL=nx.directed_laplacian_matrix(G2) 
  58. print('\n有向拉普拉斯矩陣:\n',DL) 
  59.  
  60. #拉普拉斯算子的特征值 
  61. LS=nx.laplacian_spectrum(G1) 
  62. print('\n拉普拉斯算子的特征值:\n',LS) 
  63.  
  64. #鄰接矩陣的特征值 
  65. AS=nx.adjacency_spectrum(G1) 
  66. print('\n鄰接矩陣的特征值:\n',AS) 
  67.  
  68. #無向圖的代數連通性 
  69. AC=nx.algebraic_connectivity(G1) 
  70. print('\n無向圖的代數連通性:\n',AC) 
  71.  
  72. #圖的光譜排序 
  73. SO=nx.spectral_ordering(G1) 
  74. print('\n圖的光譜排序:\n',SO) 
  75.  
  76. #兩個矩陣的解釋看:https://blog.csdn.net/Hanging_Gardens/article/details/55670356 

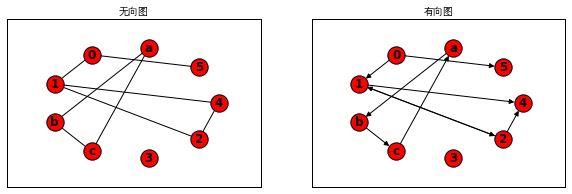
圖矩陣示例
圖矩陣示例

輸出:

  1. 鄰接矩陣: 
  2. [[0. 0. 0. 0. 5. 0. 0. 0. 6. ] 
  3. [0. 0. 0. 2. 0. 0. 0. 0. 0. ] 
  4. [0. 0. 0. 0. 0. 0.5 0.5 0. 0. ] 
  5. [0. 2. 0. 1. 1. 0. 0. 0. 0. ] 
  6. [5. 0. 0. 1. 0. 0. 0. 0. 7. ] 
  7. [0. 0. 0.5 0. 0. 0. 0.5 0. 0. ] 
  8. [0. 0. 0.5 0. 0. 0.5 0. 0. 0. ] 
  9. [0. 0. 0. 0. 0. 0. 0. 0. 0. ] 
  10. [6. 0. 0. 0. 7. 0. 0. 0. 0. ]] 
  11.  
  12. 關聯矩陣: 
  13. [[1. 1. 0. 0. 0. 0. 0. 0. 0.] 
  14. [0. 0. 1. 0. 0. 0. 0. 0. 0.] 
  15. [0. 0. 0. 1. 1. 0. 0. 0. 0.] 
  16. [0. 0. 1. 0. 0. 1. 0. 0. 0.] 
  17. [0. 1. 0. 0. 0. 1. 0. 1. 0.] 
  18. [0. 0. 0. 1. 0. 0. 0. 0. 1.] 
  19. [0. 0. 0. 0. 1. 0. 0. 0. 1.] 
  20. [0. 0. 0. 0. 0. 0. 0. 0. 0.] 
  21. [1. 0. 0. 0. 0. 0. 0. 1. 0.]] 
  22.  
  23. 拉普拉斯矩陣: 
  24. [[11. 0. 0. 0. -5. 0. 0. 0. -6. ] 
  25. [ 0. 2. 0. -2. 0. 0. 0. 0. 0. ] 
  26. [ 0. 0. 1. 0. 0. -0.5 -0.5 0. 0. ] 
  27. [ 0. -2. 0. 3. -1. 0. 0. 0. 0. ] 
  28. [-5. 0. 0. -1. 13. 0. 0. 0. -7. ] 
  29. [ 0. 0. -0.5 0. 0. 1. -0.5 0. 0. ] 
  30. [ 0. 0. -0.5 0. 0. -0.5 1. 0. 0. ] 
  31. [ 0. 0. 0. 0. 0. 0. 0. 0. 0. ] 
  32. [-6. 0. 0. 0. -7. 0. 0. 0. 13. ]] 
  33.  
  34. 標准化的拉普拉斯矩陣: 
  35. [[ 1. 0. 0. 0. -0.418 0. 0. 0. -0.502] 
  36. [ 0. 1. 0. -0.707 0. 0. 0. 0. 0. ] 
  37. [ 0. 0. 1. 0. 0. -0.5 -0.5 0. 0. ] 
  38. [ 0. -0.707 0. 0.75 -0.139 0. 0. 0. 0. ] 
  39. [-0.418 0. 0. -0.139 1. 0. 0. 0. -0.538] 
  40. [ 0. 0. -0.5 0. 0. 1. -0.5 0. 0. ] 
  41. [ 0. 0. -0.5 0. 0. -0.5 1. 0. 0. ] 
  42. [ 0. 0. 0. 0. 0. 0. 0. 0. 0. ] 
  43. [-0.502 0. 0. 0. -0.538 0. 0. 0. 1. ]] 
  44.  
  45. 有向拉普拉斯矩陣: 
  46. [[ 0.889 -0.117 -0.029 -0.087 -0.319 -0.029 -0.029 -0.129 -0.242] 
  47. [-0.117 0.889 -0.026 -0.278 -0.051 -0.026 -0.026 -0.114 -0.056] 
  48. [-0.029 -0.026 0.994 -0.012 -0.009 -0.481 -0.481 -0.025 -0.01 ] 
  49. [-0.087 -0.278 -0.012 0.757 -0.097 -0.012 -0.012 -0.052 -0.006] 
  50. [-0.319 -0.051 -0.009 -0.097 0.994 -0.009 -0.009 -0.041 -0.434] 
  51. [-0.029 -0.026 -0.481 -0.012 -0.009 0.994 -0.481 -0.025 -0.01 ] 
  52. [-0.029 -0.026 -0.481 -0.012 -0.009 -0.481 0.994 -0.025 -0.01 ] 
  53. [-0.129 -0.114 -0.025 -0.052 -0.041 -0.025 -0.025 0.889 -0.045] 
  54. [-0.242 -0.056 -0.01 -0.006 -0.434 -0.01 -0.01 -0.045 0.994]] 
  55.  
  56. 拉普拉斯算子的特征值: 
  57. [-1.436e-15 0.000e+00 4.610e-16 7.000e-01 1.500e+00 1.500e+00 
  58. 4.576e+00 1.660e+01 2.013e+01] 
  59.  
  60. 鄰接矩陣的特征值: 
  61. [12.068+0.000e+00j 2.588+0.000e+00j -7.219+0.000e+00j -4.925+0.000e+00j 
  62. -1.513+0.000e+00j 1. +0.000e+00j -0.5 +2.393e-17j -0.5 -2.393e-17j 
  63. 0. +0.000e+00j] 
  64.  
  65. 無向圖的代數連通性: 
  66. 0.0 
  67.  
  68. 圖的光譜排序: 
  69. ['4', '2', '1', '0', '5', 'b', 'c', 'a', '3'] 

后面還有兩個小節,由於對圖論算法不是很明白,所以先講明白算法原理,再使用networkX實現,如無須讀算法,可以跳過算法原理部分.


免責聲明！

本站轉載的文章為個人學習借鑒使用，本站對版權不負任何法律責任。如果侵犯了您的隱私權益，請聯系本站郵箱yoyou2525@163.com刪除。



猜您在找 線性代數相關算法小記 【線性代數的本質 - 系列合集】矩陣與線性變換 線性代數及其應用（一） 線性代數總結 線性代數基礎 線性代數 線性代數入門 線性代數 線性代數 [線性代數] 線性代數入門A Gentle Introduction
 
粵ICP備18138465號   © 2018-2025 CODEPRJ.COM