矩陣的乘法

定義

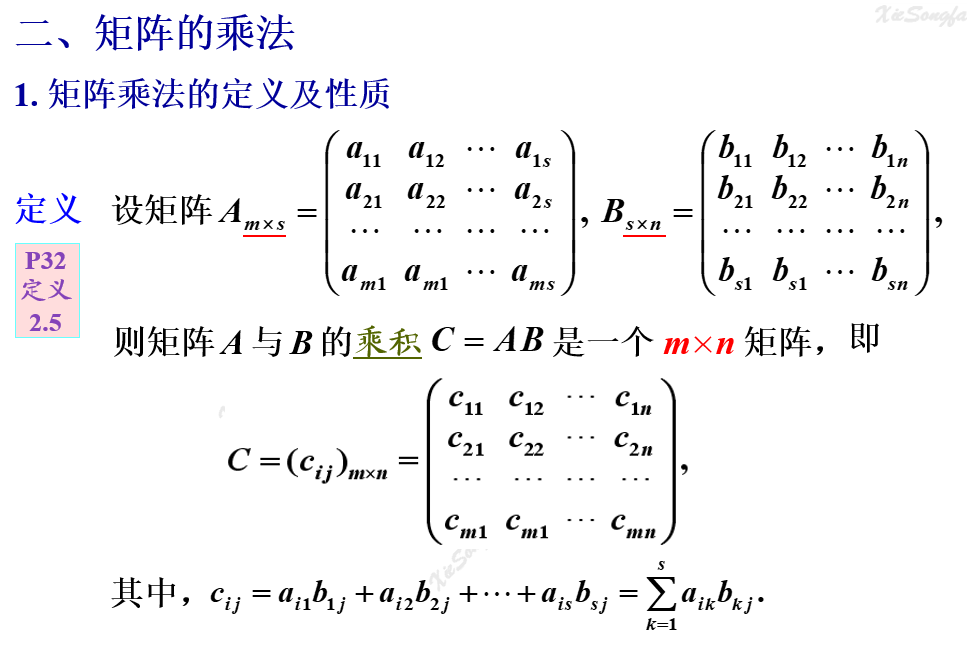
注意，上面的圖片中，\(A_{m \times s}\) 和 \(B_{s \times n}\) 和 \(C\) 中最后一行的第 2 個數的下標右一點小錯誤，不過，無傷大雅。

java 代碼實現：

/**
 * 求解矩陣的乘法
 * @param m1 矩陣，格式為 m 行乘以 s 列
 * @param m2 矩陣，格式為 s 行乘以 n 列
 * @return 一個 m 乘以 n 的矩陣
 */
public int[][] multiMatrix(int[][] m1, int[][] m2) {
    int[][] res = new int[m1.length][m2[0].length];
    for (int i = 0; i < m1.length; i++) {
        for (int j = 0; j < m2[0].length; j++) {
            for (int k = 0; k < m2.length; k++) {
                res[i][j] += m1[i][k] * m2[k][j];
            }
        }
    }
    return res;
}

測試：

public static void main(String[] args) {
    Matrix matrix = new Matrix();
    int[][] m1 = {{4, 3, 1},
                  {2, 1, 3},
                  {3, 1, 2}};
    int[][] m2 = {{2,2},
                  {1,3},
                  {0,1}};
    int[][] res = matrix.multiMatrix(m1, m2);
    for (int i = 0; i < res.length; i++) {
        for (int j = 0; j < res[0].length; j++) {
            System.out.print(res[i][j] + " ");
        }
        System.out.println();
    }
}

輸出結果：

11 18
5 10
7 11

上面的測試用例對應下面的示例：

方陣的乘冪

注意，我們平時說的矩陣的乘冪，是特指方陣的乘冪。