泊松分布的定義
設隨機變量 X 所有可能取的值為 0 , 1, 2, ... , 且取各個值的概率為:
\[P(X = k) = e^{-\lambda}\displaystyle\frac{\lambda^k}{k!}, \ k = 0, 1, 2,..., \]
其中,\(\lambda > 0\) 是常數,則稱 X 服從參數為 \(\lambda\) 的泊松分布,記作 \(X \sim P(\lambda)\).
指數分布的定義
若連續型隨機變量 X 的概率密度為:
\[f(x) = \begin{cases} \lambda e^{-\lambda x}, \quad x > 0 \\ 0, \quad \quad \quad x \leq 0 \end{cases} \]
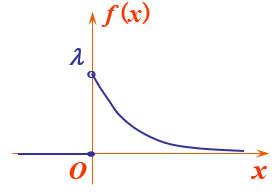
其中 \(\lambda > 0\) 為常數,則稱 X 服從參數 \(\lambda\) 的指數分布,記為 \(X \sim E(\lambda)\).
指數分布的函數:
\[F(x) = \begin{cases} 1 - e^{-\lambda x}, \quad x > 0 \\ 0, \quad \quad \quad \quad x \leq 0 \end{cases} \]
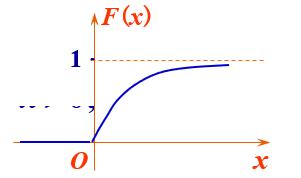
指數分布與泊松流的關系
在泊松流中,記時間間隔 \((0, t]\) 中出現的質點數為 X

則 \(X \sim P(\lambda t)\),即有:
\[P \{ X = k \} = \displaystyle\frac{{(\lambda t)}^k}{k!} e^{- \lambda t}, \ k = 0,1,2,... \]
其中參數 \(\lambda\) 稱為泊松強度.
記 \(T\) 表示第一個質點出現的時間,則 ${ T > t } \Leftrightarrow $ 在 \((0, t]\) 內沒有粒子到達 \(P \{ T > t \} = P \{ X = 0 \} = e^{- \lambda t}\),即 \(T\) 的分布函數為
\[F(t) = P \{T \leq t \} = 1 - e^{- \lambda t} \quad (t > 0) \]
\[\therefore Y \sim E(\lambda) \]
注:上面的泊松流指的應該(不確定)是泊松過程:

