TOPSIS算法

---

title: TOPSIS算法
date: 2020-02-24 11:18:06
categories: 數學建模
tags: [評價模型, MATLAB]
mathjax: true

---

定義

​ C.L.Hwang和K.Yoon於1981年首次提出TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution)，可翻譯為逼近理 想解排序法，國內常簡稱為優劣解距離法。

​ TOPSIS 法是一種常用的綜合評價方法，能充分利用原始數據的 信息，其結果能精確地反映各評價方案之間的差距。

​ 基本過程為先將原始數據矩陣統一指標類型（一般正向化處理） 得到正向化的矩陣，再對正向化的矩陣進行標准化處理以消除各指 標量綱的影響，並找到有限方案中的最優方案和最劣方案，然后分 別計算各評價對象與最優方案和最劣方案間的距離，獲得各評價對 象與最優方案的相對接近程度，以此作為評價優劣的依據。該方法對數據分布及樣本含量沒有嚴格限制，數據計算簡單易行。

例子

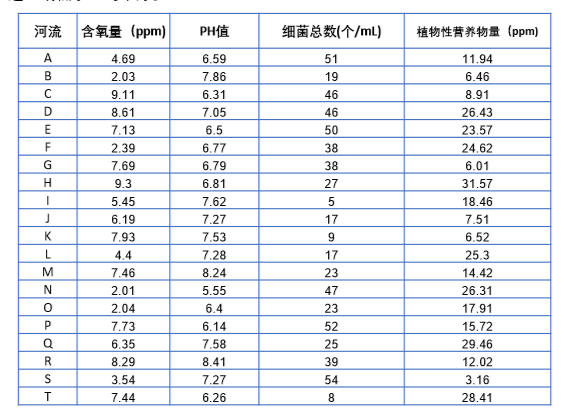
評價下表中20條河流的水質情況。 注：含氧量越高越好；PH值越接近7越好；細菌總數越少越好；植物性營養物量介於10‐20之間最佳，超 過20或低於10均不好。

步驟

第一步：將原始矩陣正向化

最常見的四種指標：

指標名稱	指標特點	例子
極大型（效益型）指標	越大（多）越好	成績、GDP增速、企業利潤
極小型（成本型）指標	越小（少）越好	費用、壞品率、污染程度
中間型指標	越接近某個值越好	水質量評估時的PH值
區間型指標	落在某個區間最好	體溫、水中植物性營養物量

所謂的將原始矩陣正向化，就是要將所有的指標類型統一轉化為 極大型指標。（轉換的函數形式可以不唯一 ）

極小型指標->極大型指標

極小型指標轉換為極大型指標的公式：

\[max-x \]

如果所有的元素均為正數，那么也可以使用 1/x

中間型指標->極大型指標

{\(x_{i}\)}是一組中間型指標序列，且最佳的數值為\(x_{best}\)，那么正向化的公式如下：

\[M=\max \left\{\left|x_{i}-x_{\text {best}}\right|\right\}, \quad \tilde{x}_{i}=1-\frac{\left|x_{i}-x_{\text {best}}\right|}{M} \]

舉個例子：

區間型指標->極大型指標

{\(x_{i}\)}是一組中間型指標序列，且最佳的區間為[a，b]，那么正向化的公式如下：

\[M=\max \left\{a-\min \left\{x_{i}\right\}, \max \left\{x_{i}\right\}-b\right\}, \quad \tilde{x}_{i}=\left\{\begin{array}{ll} {1-\frac{a-x}{M}} & {, x<a} \\ {1} & {, a \leq x \leq b} \\ {1-\frac{x-b}{M}} & {, x>b} \end{array}\right. \]

第二步：正向化矩陣標准化

為了消去不同指標量綱的影響， 需要對已經正向化的矩陣進行標准化處理。

假設有n個要評價的對象，m個評價指標（已經正向化了）構成的正向化矩陣如下：

\[A=\begin{bmatrix}a_{11}& a_{12}& \cdots & a_{1n}\\a_{21}& a_{22}& \cdots & a_{2n}\\\vdots & \vdots & \ddots & \vdots \\a_{m1}& a_{m2}& \cdots & a_{mn}\end{bmatrix} \]

那么，對其標准化的矩陣記為Z，Z中的每一個元素：

\[z_{ij}=a_{ij}/ \sqrt{\sum_{i=1}^{n}a_{ij}^{2} } \]

\[每一個元素/\sqrt{V其所在列的元素的平方和} \]

注意：標准化的方法有很多種，其主要目的就是去除量綱的影響，未來我們還可能見到更多 種的標准化方法，例如：(x‐x的均值)/x的標准差；具體選用哪一種標准化的方法在多數情況下 並沒有很大的限制，這里我們采用的是前人的論文中用的比較多的一種標准化方法。

第三步：計算得分並歸一化

計算評分的公式

\[\frac{x-min}{max-min} \]

解釋原因

（1）比較的對象一般要遠大於兩個。（例如比較一個班級的成績）
（2）比較的指標也往往不只是一個方面的，例如成績、工時數、課 外競賽得分等。
（3）有很多指標不存在理論上的最大值和最小值，例如衡量經濟增 長水平的指標：GDP增速

更深本質

\[\frac{x-min}{max-min}=\frac{x-min}{(max-x)+(x-min)}\\ =\frac{x與最小值的距離}{x與最大值的距離+x與最小值的距離} \]

注意：要區別開歸一化和標准化。歸一化的計算步驟也可以 消去量綱的影響，但更多時候，我們進行歸一化的目的是為 了讓我們的結果更容易解釋，或者說讓我們對結果有一個更 加清晰直觀的印象。例如將得分歸一化后可限制在0‐1這個區 間，對於區間內的每一個得分，我們很容易的得到其所處的比例位置。

可以使用層次分析法給這m個評價指標確定權重：

\[\sum_{j=1}^{m}w_{j}=1 \]

層次分析法的主觀性太強了，更推薦大家使用熵權法來進行客觀賦值

代碼

topsis.m

%%  第一步：把數據復制到工作區，並將這個矩陣命名為X
% （1）在工作區右鍵，點擊新建（Ctrl+N)，輸入變量名稱為X
% （2）在Excel中復制數據，再回到Excel中右鍵，點擊粘貼Excel數據（Ctrl+Shift+V）
% （3）關掉這個窗口，點擊X變量，右鍵另存為，保存為mat文件（下次就不用復制粘貼了，只需使用load命令即可加載數據）
% （4）注意，代碼和數據要放在同一個目錄下哦，且Matlab的當前文件夾也要是這個目錄。
clear;clc
load data_water_quality.mat
%% 注意：如果提示: 錯誤使用 load，無法讀取文件 'data_water_quality.mat'。沒有此類文件或目錄。
% 那么原因是因為你的Matlab的當前文件夾中不存在這個文件
% 可以使用cd函數修改Matlab的當前文件夾
% 比如說，我的代碼和數據放在了: D:第2講.TOPSIS法（優劣解距離法）\代碼和例題數據
% 那么我就可以輸入命令：
% cd 'D:第2講.TOPSIS法（優劣解距離法）\代碼和例題數據'
% 也可以看我更新的視頻：“更新9_Topsis代碼為什么運行失敗_得分結果怎么可視化以及權重的確定如何更加准確”，里面有介紹

%%  第二步：判斷是否需要正向化
[n,m] = size(X);
disp(['共有' num2str(n) '個評價對象, ' num2str(m) '個評價指標']) 
Judge = input(['這' num2str(m) '個指標是否需要經過正向化處理，需要請輸入1 ，不需要輸入0：  ']);

if Judge == 1
    Position = input('請輸入需要正向化處理的指標所在的列，例如第2、3、6三列需要處理，那么你需要輸入[2,3,6]： '); %[2,3,4]
    disp('請輸入需要處理的這些列的指標類型（1：極小型， 2：中間型， 3：區間型） ')
    Type = input('例如：第2列是極小型，第3列是區間型，第6列是中間型，就輸入[1,3,2]：  '); %[2,1,3]
    % 注意，Position和Type是兩個同維度的行向量
    for i = 1 : size(Position,2)  %這里需要對這些列分別處理，因此我們需要知道一共要處理的次數，即循環的次數
        X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
    % Positivization是我們自己定義的函數，其作用是進行正向化，其一共接收三個參數
    % 第一個參數是要正向化處理的那一列向量 X(:,Position(i))   回顧上一講的知識，X(:,n)表示取第n列的全部元素
    % 第二個參數是對應的這一列的指標類型（1：極小型， 2：中間型， 3：區間型）
    % 第三個參數是告訴函數我們正在處理的是原始矩陣中的哪一列
    % 該函數有一個返回值，它返回正向化之后的指標，我們可以將其直接賦值給我們原始要處理的那一列向量
    end
    disp('正向化后的矩陣 X =  ')
    disp(X)
end
%% 作業：在這里增加是否需要算加權
% 補充一個基礎知識：m*n維的矩陣A 點乘 n維行向量B，等於這個A的每一行都點乘B
% （注意：2017以及之后版本的Matlab才支持，老版本Matlab會報錯）
% % 假如原始數據為：
%   A=[1, 2, 3;
%        2, 4, 6] 
% % 權重矩陣為：
%   B=[ 0.2, 0.5 ,0.3 ] 
% % 加權后為：
%   C=A .* B
%     0.2000    1.0000    0.9000
%     0.4000    2.0000    1.8000
% 類似的，還有矩陣和向量的點除， 大家可以自己試試計算A ./ B
% 注意，矩陣和向量沒有 .- 和 .+ 哦 ，大家可以試試，如果計算A.+B 和 A.-B會報什么錯誤。

%% 這里補充一個小插曲
% % 在上一講層次分析法的代碼中，我們可以優化以下的語句：
% % Sum_A = sum(A);
% % SUM_A = repmat(Sum_A,n,1);
% % Stand_A = A ./ SUM_A;
% % 事實上，我們把第三行換成：Stand_A = A ./ Sum_A; 也是可以的哦 
% % (再次強調，新版本的Matlab才能運行哦)

%% 讓用戶判斷是否需要增加權重
disp("請輸入是否需要增加權重向量，需要輸入1，不需要輸入0")
Judge = input('請輸入是否需要增加權重： ');
if Judge == 1
    disp(['如果你有3個指標，你就需要輸入3個權重，例如它們分別為0.25,0.25,0.5, 則你需要輸入[0.25,0.25,0.5]']);
    weigh = input(['你需要輸入' num2str(m) '個權數。' '請以行向量的形式輸入這' num2str(m) '個權重: ']);
    OK = 0;  % 用來判斷用戶的輸入格式是否正確
    while OK == 0 
        if abs(sum(weigh) - 1)<0.000001 && size(weigh,1) == 1 && size(weigh,2) == m   % 這里要注意浮點數的運算是不精准的。
             OK =1;
        else
            weigh = input('你輸入的有誤，請重新輸入權重行向量: ');
        end
    end
else
    weigh = ones(1,m) ./ m ; %如果不需要加權重就默認權重都相同，即都為1/m
end


%% 第三步：對正向化后的矩陣進行標准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('標准化矩陣 Z = ')
disp(Z)

%% 第四步：計算與最大值的距離和最小值的距離，並算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ] .* repmat(weigh,n,1) ,2) .^ 0.5;   % D+ 與最大值的距離向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ] .* repmat(weigh,n,1) ,2) .^ 0.5;   % D- 與最小值的距離向量
S = D_N ./ (D_P+D_N);    % 未歸一化的得分
disp('最后的得分為：')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')

% A = magic(5)  % 幻方矩陣
% M = magic(n)返回由1到n^2的整數構成並且總行數和總列數相等的n×n矩陣。階次n必須為大於或等於3的標量。
% sort(A)若A是向量不管是列還是行向量，默認都是對A進行升序排列。sort(A)是默認的升序，而sort(A,'descend')是降序排序。
% sort(A)若A是矩陣，默認對A的各列進行升序排列
% sort(A,dim)
% dim=1時等效sort(A)
% dim=2時表示對A中的各行元素升序排列
% A = [2,1,3,8]
% Matlab中給一維向量排序是使用sort函數：sort（A），排序是按升序進行的，其中A為待排序的向量；
% 若欲保留排列前的索引，則可用 [sA,index] = sort(A,'descend') ，排序后，sA是排序好的向量，index是向量sA中對A的索引。
% sA  =  8     3     2     1
% index =  4     3     1     2

Inter2Max.m

function [posit_x] = Inter2Max(x,a,b)
    r_x = size(x,1);  % row of x 
    M = max([a-min(x),max(x)-b]);
    posit_x = zeros(r_x,1);   %zeros函數用法: zeros(3)  zeros(3,1)  ones(3)
    % 初始化posit_x全為0  初始化的目的是節省處理時間
    for i = 1: r_x
        if x(i) < a
           posit_x(i) = 1-(a-x(i))/M;
        elseif x(i) > b
           posit_x(i) = 1-(x(i)-b)/M;
        else
           posit_x(i) = 1;
        end
    end
end

Mid2Max.m

function [posit_x] = Mid2Max(x,best)
    M = max(abs(x-best));
    posit_x = 1 - abs(x-best) / M;
end

Min2Max.m

function [posit_x] = Min2Max(x)
    posit_x = max(x) - x;
     %posit_x = 1 ./ x;    %如果x全部都大於0，也可以這樣正向化
end

Positivization.m

% function [輸出變量] = 函數名稱(輸入變量）  
% 函數的中間部分都是函數體
% 函數的最后要用end結尾
% 輸出變量和輸入變量可以有多個，用逗號隔開
% function [a,b,c]=test(d,e,f)
%     a=d+e;
%     b=e+f;
%     c=f+d;
% end
% 自定義的函數要單獨放在一個m文件中，不可以直接放在主函數里面（和其他大多數語言不同）

function [posit_x] = Positivization(x,type,i)
% 輸入變量有三個：
% x：需要正向化處理的指標對應的原始列向量
% type： 指標的類型（1：極小型， 2：中間型， 3：區間型）
% i: 正在處理的是原始矩陣中的哪一列
% 輸出變量posit_x表示：正向化后的列向量
    if type == 1  %極小型
        disp(['第' num2str(i) '列是極小型，正在正向化'] )
        posit_x = Min2Max(x);  %調用Min2Max函數來正向化
        disp(['第' num2str(i) '列極小型正向化處理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界線~~~~~~~~~~~~~~~~~~~~')
    elseif type == 2  %中間型
        disp(['第' num2str(i) '列是中間型'] )
        best = input('請輸入最佳的那一個值： ');
        posit_x = Mid2Max(x,best);
        disp(['第' num2str(i) '列中間型正向化處理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界線~~~~~~~~~~~~~~~~~~~~')
    elseif type == 3  %區間型
        disp(['第' num2str(i) '列是區間型'] )
        a = input('請輸入區間的下界： ');
        b = input('請輸入區間的上界： '); 
        posit_x = Inter2Max(x,a,b);
        disp(['第' num2str(i) '列區間型正向化處理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界線~~~~~~~~~~~~~~~~~~~~')
    else
        disp('沒有這種類型的指標，請檢查Type向量中是否有除了1、2、3之外的其他值')
    end
end

結果

正向化后的矩陣 X =  
    4.6900    0.7172    3.0000    1.0000
    2.0300    0.4069   35.0000    0.6940
    9.1100    0.5241    8.0000    0.9058
    8.6100    0.9655    8.0000    0.4443
    7.1300    0.6552    4.0000    0.6914
    2.3900    0.8414   16.0000    0.6007
    7.6900    0.8552   16.0000    0.6551
    9.3000    0.8690   27.0000         0
    5.4500    0.5724   49.0000    1.0000
    6.1900    0.8138   37.0000    0.7848
    7.9300    0.6345   45.0000    0.6992
    4.4000    0.8069   37.0000    0.5419
    7.4600    0.1448   31.0000    1.0000
    2.0100         0    7.0000    0.4546
    2.0400    0.5862   31.0000    1.0000
    7.7300    0.4069    2.0000    1.0000
    6.3500    0.6000   29.0000    0.1824
    8.2900    0.0276   15.0000    1.0000
    3.5400    0.8138         0    0.4088
    7.4400    0.4897   46.0000    0.2731

請輸入是否需要增加權重向量，需要輸入1，不需要輸入0
請輸入是否需要增加權重： 1
如果你有3個指標，你就需要輸入3個權重，例如它們分別為0.25,0.25,0.5, 則你需要輸入[0.25,0.25,0.5]
你需要輸入4個權數。請以行向量的形式輸入這4個權重: [0.25,0.25,0.25,0.25]
標准化矩陣 Z = 
    0.1622    0.2483    0.0245    0.3065
    0.0702    0.1408    0.2863    0.2127
    0.3150    0.1814    0.0655    0.2776
    0.2977    0.3342    0.0655    0.1361
    0.2466    0.2268    0.0327    0.2119
    0.0826    0.2912    0.1309    0.1841
    0.2659    0.2960    0.1309    0.2008
    0.3216    0.3008    0.2209         0
    0.1885    0.1981    0.4009    0.3065
    0.2141    0.2817    0.3027    0.2405
    0.2742    0.2196    0.3682    0.2143
    0.1522    0.2793    0.3027    0.1661
    0.2580    0.0501    0.2536    0.3065
    0.0695         0    0.0573    0.1393
    0.0705    0.2029    0.2536    0.3065
    0.2673    0.1408    0.0164    0.3065
    0.2196    0.2077    0.2373    0.0559
    0.2867    0.0095    0.1227    0.3065
    0.1224    0.2817         0    0.1253
    0.2573    0.1695    0.3763    0.0837

最后的得分為：

stand_S =

    0.0451
    0.0478
    0.0485
    0.0488
    0.0431
    0.0448
    0.0539
    0.0510
    0.0681
    0.0684
    0.0702
    0.0591
    0.0527
    0.0192
    0.0533
    0.0434
    0.0466
    0.0438
    0.0358
    0.0565


sorted_S =

    0.0702
    0.0684
    0.0681
    0.0591
    0.0565
    0.0539
    0.0533
    0.0527
    0.0510
    0.0488
    0.0485
    0.0478
    0.0466
    0.0451
    0.0448
    0.0438
    0.0434
    0.0431
    0.0358
    0.0192


index =

    11
    10
     9
    12
    20
     7
    15
    13
     8
     4
     3
     2
    17
     1
     6
    18
    16
     5
    19
    14