問題
在一個圓環上隨機取3點,求這3個點組成一個銳角三角形的概率
題解
如下圖所示:
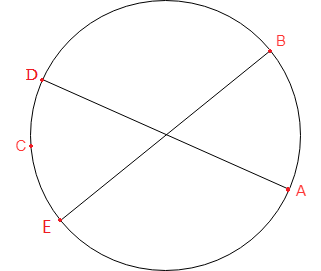
取單位圓上任意不同兩點A和B,A、B兩點確定以后,點A、B、C三點要夠成銳角三角形,點C必須在DE之間,否在將構成直角三角形(點C與點D或點E重合)或鈍角三角形。設AB弧所對應的圓心角為\(\theta\),則當且僅當\(\theta \in (0, \pi)\) 時有可能構成銳角三角形。\(\theta\) 的概率密度是 \(\frac{1}{\pi}\),此時組成銳角三角形需要C點在AB對應的DE段間的概率是 \(\frac{\theta}{2\pi}\)。故在一個圓環上隨機添加3點,三個點組成一個銳角三角形的概率為
\[\int_0^\pi \frac{1}{\pi}\cdot\frac{\theta}{2\pi}\mathrm{d}\theta = \frac{\theta ^ 2}{4\pi ^ 2}\bigg|_0^\pi = \frac{1}{4} \]
Python 代碼模擬
#! /usr/bin/env python3
# -*- coding: utf-8 -*-
# @Author: wzdnzd
import numpy as np
def simulate(n):
# 圓心角θ所對應的弦長 l = 2 * R * sin(θ/2), R為圓的半徑
def compute(theta):
if theta > np.pi:
theta = 2 * np.pi - theta
return 2 * np.sin(theta / 2)
# 根據三角形三條邊的平方關系判斷是否是銳角、直角或鈍角三角形
def judge(array):
if len(array) != 3:
raise ValueError('len(array) must be 3.')
if array[0] ** 2 + array[1] ** 2 > array[2] ** 2:
return -1
elif array[0] ** 2 + array[1] ** 2 == array[2] ** 2:
return 0
else:
return 1
acute, right, obtuse = 0, 0, 0
for _ in range(n):
angles = sorted(np.random.rand(3) * 2 * np.pi)
chords = sorted([compute(angles[1] - angles[0]),
compute(angles[2] - angles[1]),
compute(2 * np.pi + angles[0] - angles[2])])
flag = judge(chords)
if flag == -1:
acute += 1
elif flag == 0:
right += 1
else:
obtuse += 1
return [x / n for x in [acute, right, obtuse]]
if __name__ == "__main__":
probabilities = simulate(100000)
print('acute: {}\tright: {}\tobtuse: {}'.format(
probabilities[0], probabilities[1], probabilities[2]))
運行結果如下:
acute: 0.25009 right: 0.0 obtuse: 0.74991
