假設檢驗（Hypothesis Testing）

假設檢驗的定義

假設檢驗：先對總體參數提出某種假設，然后利用樣本數據判斷假設是否成立。在邏輯上，假設檢驗采用了反證法，即先提出假設，再通過適當的統計學方法證明這個假設基本不可能是真的。（說“基本”是因為統計得出的結果來自於隨機樣本，結論不可能是絕對的，所以我們只能根據概率上的一些依據進行相關的判斷。）

 

假設檢驗依據的是小概率思想，即小概率事件在一次試驗中基本上不會發生。

 

如果樣本數據拒絕該假設，那么我們說該假設檢驗結果具有統計顯著性。一項檢驗結果在統計上是“顯著的”，意思是指樣本和總體之間的差別不是由於抽樣誤差或偶然而造成的。

 

假設檢驗的術語

零假設（null hypothesis）：是試驗者想收集證據予以反對的假設，也稱為原假設，通常記為 H₀。

例如：零假設是測試版本的指標均值小於等於原始版本的指標均值。

 

備擇假設（alternative hypothesis）：是試驗者想收集證據予以支持的假設，通常記為H₁或 H_a。

例如：備擇假設是測試版本的指標均值大於原始版本的指標均值。

 

雙尾檢驗（two-tailed test）：如果備擇假設沒有特定的方向性，並含有符號“≠”，這樣的檢驗稱為雙尾檢驗。

例如：零假設是測試版本的指標均值等於原始版本的指標均值，備擇假設是測試版本的指標均值不等於原始版本的指標均值。

 

單尾檢驗（one-tailed test）：如果備擇假設具有特定的方向性，並含有符號 “>” 或 “<” ，這樣的檢驗稱為單尾檢驗。單尾檢驗分為左尾（lower tail）和右尾（upper tail）。

例如：零假設是測試版本的指標均值小於等於原始版本的指標均值，備擇假設是測試版本的指標均值大於原始版本的指標均值。

 

檢驗統計量（test statistic）：用於假設檢驗計算的統計量。

例如：Z值、t值、F值、卡方值。

 

顯著性水平（level of significance）：當零假設為真時，錯誤拒絕零假設的臨界概率，即犯第一類錯誤的最大概率，用α表示。

例如：在5%的顯著性水平下，樣本數據拒絕原假設。

 

置信度（confidence level）：置信區間包含總體參數的確信程度，即1-α。

例如：95%的置信度表明有95%的確信度相信置信區間包含總體參數（假設進行100次抽樣，有95次計算出的置信區間包含總體參數）。

 

置信區間（confidence interval）：包含總體參數的隨機區間。

 

功效（power）：正確拒絕零假設的概率，即1-β。當檢驗結果是不能拒絕零假設，人們又需要進行決策時，需要關注功效。功效越大，犯第二類錯誤的可能性越小。

 

臨界值（critical value）：與檢驗統計量的具體值進行比較的值。是在概率密度分布圖上的分位數。這個分位數在實際計算中比較麻煩，它需要對數據分布的密度函數積分來獲得。

 

臨界區域（critical region）：拒絕原假設的檢驗統計量的取值范圍，也稱為拒絕域（rejection region），是由一組臨界值組成的區域。如果檢驗統計量在拒絕域內，那么我們拒絕原假設。

 

p值（p-value）：在零假設為真時所得到的樣本觀察結果或獲得更極端結果的概率。也可以說，p值是當原假設為真時，錯誤拒絕原假設的實際概率。

左尾檢驗的P值為檢驗統計量x小於樣本統計值C的概率，即：p = P( x < C)
右尾檢驗的P值為檢驗統計量x大於樣本統計值C的概率，即：p = P( x > C)
雙尾檢驗的P值為檢驗統計量x落在樣本統計值C為端點的尾部區域內的概率的2倍，即：p = 2P( x > C) (當C位於分布曲線的右端時) 或p = 2P( X< C) (當C 位於分布曲線的左端時) 。

 

效應量（effect size）：樣本間差異或相關程度的量化指標。效應量越大，兩組平均數離得越遠，差異越大。如果結果具有統計顯著性，那么有必要報告效應量的大小。效應量太小，意味着即使結果有統計顯著性，也缺乏實用價值。

 

假設檢驗的兩類錯誤

第 I 類錯誤(棄真錯誤)：零假設為真時錯誤地拒絕了零假設。犯第 I 類錯誤的最大概率記為 α（alpha）。

第 II 類錯誤(取偽錯誤)：零假設為假時錯誤地接受了零假設。犯第 II 類錯誤的最大概率記為 β（beta）。

 

在假設檢驗中，我們可能在決策上犯這兩類錯誤。一般來說，在樣本量確定的情況下，任何決策無法同時避免這兩類錯誤的發生，即在減少第一類錯誤發生的同時，會增大第二類錯誤發生的幾率，或者在減少第二類錯誤發生的同時，會增大第一類錯誤發生的幾率。

 

在大多數情況下，人們會控制第一類錯誤發生的概率。在進行假設檢驗時，人們通過事先給定顯著性水平α的值來控制第一類錯誤發生的概率，常用的 α 值有 0.01，0.05，0.1。如果犯第一類錯誤的成本不高，那么可以選擇較大的α值；如果犯第一類錯誤的成本很高，則選擇較小的α值。

 

注：人們將只控制第一類錯誤的假設檢驗稱為顯著性檢驗，許多假設檢驗的應用都屬於這一類型。

 

假設檢驗的步驟

1，定義總體

2，確定原假設和備擇假設

3，選擇檢驗統計量（確定假設檢驗的種類）

4，選擇顯著性水平

5，從總體進行抽樣，得到一定的數據

6，根據樣本數據計算檢驗統計量的具體值

7，依據所構造的檢驗統計量的抽樣分布和顯著性水平，確定臨界值和拒絕域

8，比較檢驗統計量的值與臨界值，如果檢驗統計量的值在拒絕域內，則拒絕原假設

 

假設檢驗的決策標准

由於檢驗是利用事先給定顯著性水平的方法來控制犯錯概率的，所以對於兩個數據比較相近的假設檢驗，我們無法知道哪一個假設更容易犯錯，即我們通過這種方法只能知道根據這次抽樣而犯第一類錯誤的最大概率，而無法知道具體在多大概率水平上犯錯。計算P值有效的解決了這個問題，P值其實就是按照抽樣分布計算的一個概率值，這個值是根據檢驗統計量計算出來的。通過直接比較P值與給定的顯著性水平α的大小就可以知道是否拒絕原假設，顯然這就可以代替比較檢驗統計量的具體值與臨界值的大小的方法。而且通過這種方法，我們還可以知道在P值小於α的情況下犯第一類錯誤的實際概率是多少。假如P＝0.03<α（0.05），那么拒絕假設，這一決策可能犯錯的概率就是0.03。

 

因此假設檢驗的第7,8步可以改成：7，利用檢驗統計量的具體值計算p值；8，將給定的顯著性水平α與p值比較，作出結論：如果p值<=α，則拒絕原假設。

 

附：用於解讀p值的指導意見：p值小於0.01---強有力的證據判定備擇假設為真；

                                                 p值介於0.01~0.05---有力的證據判定備擇假設為真；

                                                 p值介於0.05~0.1---較弱的證據判定備擇假設為真；

                                                 p值大於0.1---沒有足夠的證據判定備擇假設為真。

 

需要指出的是，如果p>α，那么原假設不被拒絕，在這種情況下，實際上是無法做出決策的。如果我們需要做出決策，那么此時就需要關注犯第二類錯誤的概率。當同時控制第一類錯誤和第二類錯誤發生的概率時，假設檢驗的結論就是：拒絕原假設或接受原假設。

 

假設檢驗的種類

主要包括：Z檢驗，t檢驗，卡方檢驗，F檢驗。

 

下面分別來看一下這四種假設檢驗：

 

Z檢驗（Z test）：需要事先知道總體方差，另外，如果總體不服從正態分布，那么樣本量要大於等於30，如果總體服從正態分布，那么對樣本量沒有要求。

Z檢驗用於比較樣本和總體的均值是否不同或者兩個樣本的均值是否不同。檢驗統計量z值的分布服從正態分布。

 

由於總體方差一般都是未知的，並且Z檢驗只適合大樣本的情況，而t檢驗同時適用於大樣本和小樣本的情況（至於為什么，請看：https://www.cnblogs.com/HuZihu/p/9442316.html），因此用t檢驗比較多。

 

t檢驗（t test）：事先不知道總體方差，另外，如果總體不服從正態分布，那么樣本量要大於等於30，如果總體服從正態分布，那么對樣本量沒有要求。

t檢驗分為單樣本t檢驗，配對t檢驗和獨立樣本t檢驗。

 

單樣本t檢驗（One Sample T-Test）：用樣本均值和總體均值進行比較，來檢驗樣本與總體之間的差異性。

（是隨機樣本均值，μ₀是總體均值，s是樣本標准差，n是樣本中的觀察值數量，自由度為n-1）

 

配對t檢驗（Paired Sample T-Test）：用兩個配對樣本中各對觀測值的差值均數和假設的差值進行比較，來檢驗以下幾種情形： 1，同一受試對象或兩個同質受試對象接受兩種不同處理后的差異；2，同一受試對象接受處理前后的差異。

配對t檢驗的本質是先計算成對觀測值之間的差異的均值，之后執行單樣本t檢驗。

 （d為每對數據的差值，d¯為樣本差值的均數，S_d¯為樣本差值均數的標准差，即樣本差值的標准誤差，S_d為樣本差值的標准差，n為成對觀測值的對數，自由度為n-1）

 

獨立樣本t檢驗（Independent Samples T-Test）：用從兩個不同總體抽取出的樣本的均值進行比較，來檢驗兩個總體之間的差異性。其又分為方差相等和方差不相等這兩種情況。

 

方差相等（Equal Variance or pooled T-Test）：每組數據的樣本數量相同，或者兩組數據的方差相差不大。

 

 

方差不相等（Unequal Variance T-Test）：每組數據的樣本數量不同，並且兩組數據的方差相差較大。此假設檢驗亦稱為Welch's t-test。

 

卡方檢驗（chi-square test）：卡方檢驗屬於非參數檢驗，不存在具體參數，且不需要有總體服從正態分布的假設。

卡方檢驗分為擬合優度檢驗和獨立性檢驗。

 

擬合優度檢驗（Goodness-of-Fit Test）：用樣本中各個變量的觀察頻數與期望頻數進行比較，來檢驗總體的概率分布是否服從理論概率分布。

 

擬合優度檢驗的H₀是：總體服從某個概率分布。

建立四格表，表里填寫相應的觀察頻數和期望頻數。

計算χ²值：（O代表觀察頻數，E代表期望頻數）。如果統計量（χ²）的值很小，說明觀察頻數和期望頻數之間的差別不顯著，統計量越大，差別越顯著。

根據χ²分布及自由度可以確定在H₀假設成立的情況下獲得當前檢驗統計量的值及更極端情況的概率P。如果P值很小，說明觀察值與理論值偏離程度太大，應當拒絕原假設；否則不能拒絕原假設。

 

獨立性檢驗（Independence Test）：用樣本中兩個類別型變量的觀察頻數與期望頻數進行比較，來檢驗樣本中兩個類別型變量是否相互獨立。

 

獨立性檢驗的H₀是：兩個類別型變量相互獨立。

建立列聯表，一個變量作為行，另一個變量作為列。例如：

	貓	狗	合計
男	207	282	489
女	231	242	473
合計	438	524	962

（表里填寫的是分別喜歡貓或狗的男女人數）

計算出期望頻數，期望頻數=第i行合計數*第j列合計數/樣本量。（比如，喜歡貓的男性期望頻數就是489*438/962=222.6。）

計算χ²值：（O代表觀察頻數，E代表期望頻數），df=(行數 − 1)*(列數 − 1)

根據χ²分布及自由度可以確定在H₀假設成立的情況下獲得當前統計量及更極端情況的概率P。如果P值很小，說明兩個類別變量之間有關聯，應當拒絕原假設。

 

F檢驗（F test）

F檢驗分為方差齊性檢驗和方差分析。

 

方差齊性檢驗（F-Test for Equality of Variances）：用從兩個不同總體抽取出的樣本的方差進行比較，來檢驗兩個總體的方差是否相同。

（s² 是樣本方差：）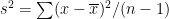

如果這兩個樣本來自於方差差不多大的總體，那么F值就會接近於1；相反，如果F值非常大，那就說明兩個總體差異較大。

 

方差齊性檢驗的前提：兩組樣本均取自正態分布的總體。（注：由於F檢驗對於數據的正態性非常敏感，因此在檢驗方差齊性的時候，Levene檢驗的穩健性要優於F檢驗。Levene檢驗也可用於多個樣本方差的比較。）

 

方差分析（Analysis of Variance，ANOVA）：用從兩個或兩個以上不同總體（各個總體的方差差不多大 ）抽取出的樣本的組內方差和組間方差進行比較，來檢驗多個總體均值的差異性。其又分為單因素方差分析和多因素方差分析。

 

這里主要說一下單因素方差分析：，即將多個樣本之間的均方差（組間均方差）除以樣本內部的均方差（組內均方差）。（其中是總均值，，k是樣本數量，N是k個樣本的總觀察值的數量）

 

方差分析的前提：總體需要滿足正態性和方差齊性。如果總體方差不齊，可以用Welch's ANOVA，具體請見：http://www.real-statistics.com/one-way-analysis-of-variance-anova/welchs-procedure/。