
文章首發於公眾號 “如風起”。
原文鏈接:
小白學統計|面板數據分析與Stata應用筆記(三)mp.weixin.qq.com

面板數據分析與Stata應用筆記整理自慕課上浙江大學方紅生教授的面板數據分析與Stata應用課程,筆記中部分圖片來自課程截圖。
筆記內容還參考了陳強教授的《高級計量經濟學及Stata應用(第二版)》
長面板數據分析
上兩篇筆記我們講到了短面板數據分析。短面板數據分析主要關注對不可觀測的個體效應的處理,而對於誤差自相關、異方差和截面相關的問題只提供經過校正的標准誤。
與短面板數據不同,長面板數據分析主要關注對誤差項的處理(因為時間T大),而將個體效應用虛擬變量來控制(因為個體n小)。
所以,對於長面板數據分析,我們不需要在固定效應模型、隨機效應模型和混合回歸模型之間進行選擇,長面板數據分析先驗假定長面板數據模型就是固定效應模型。
此外,需要注意的是,短面板數據分析對於時間效應,用虛擬變量來控制,而長面板數據分析,由於時間T相對較長,為避免損失較多的自由度,所以一般則用時間趨勢項來控制。
可以認為長面板數據模型是一個特殊的雙向固定效應模型。在這個模型中,個體效應用虛擬變量控制,時間效應用時間趨勢項控制,長面板數據模型的估計主要關注對誤差項的處理。
一、長面板數據模型的估計方法
通常有三種方法對長面板數據模型進行估計。
第一種:
使用OLS估計這個特殊的雙向固定效應模型,並對誤差項的自相關、異方差和截面相關的問題只提供面板校正的標准誤(使用命令xtscc或xtpcse命令實現),這種估計方法最為穩健。
第二種:
如果存在自相關、異方差和截面相關的問題,則使用FGLS估計這個特殊的雙向固定效應模型,這種方法只是解決了誤差項自相關的問題,而並未考慮異方差或截面相關的問題,對於誤差項的異方差和截面相關的問題仍然只是提供面板校正的標准誤(使用命令xtpcse實現),這種估計方法介於穩健和效率之間。
第三種:
使用FGLS估計這個特殊的雙向固定效應模型,對誤差項的自相關、異方差和截面相關的問題一並加以處理(使用命令xtgls實現),這種估計方法最有效率。
二、長面板數據模型的Stata估計命令
常用的估計長面板數據模型的Stata命令有三個:【xtpcse】、【xtgls】和【xtscc】
對於【xtscc】命令,我們在前兩篇短面板數據的筆記中已經講過,【xtscc】也適用於長面板數據分析,它可以實現長面板數據模型的第一種估計方法,對誤差項的自相關、異方差和截面相關問題提供面板校正的標准誤。
下面,我們講一下【xtpcse】和【xtgls】估計命令
1、【xtpcse】命令
基本命令格式:
xtpcse depvar indepvars,options
[/code]
#命令的關鍵在於選項(options),不同的選項可以處理不同的問題。
**對於誤差項三大問題【xtpcse】命令選項(options)的使用**
**(1)自相關問題(一階自相關)**
a.使用選項:corr(ar1),使用的估計方法為FGLS
#誤差項存在自相關時使用該選項;當T不比n大很多時使用該選項,因為此時T可能無法提供足夠多的信息去估計每個個體的自相關系數,所以約束了每個個體的自相關系數都相等
b.使用選項:corr(psar1),使用的估計方法為FGLS。
#誤差項存在自相關時使用該選項;當T比n大很多時使用該選擇項,當T比n大很多時每個個體的自相關系數可以不同,就可以使用選項
c.使用選項:corr(independent)或corr(ind),使用的估計方法為OLS。
#誤差項不存在自相關時,使用該選項
**(2)異方差與截面相關問題**
a.使用選項:independent
#誤差項不存在異方差和截面相關問題,使用該選項
b.使用選項:hetonly(提供考慮異方差的面板校正標准誤)
#誤差項存在異方差但不存在截面相關問題,則使用該選項
c.使用選項:不加選項即可(提供既考慮異方差又考慮截面相關的面板校正標准誤)
#誤差項存在異方差和截面相關問題時,不加任何選項
選項:corr(ind)+independent等價於LSDV
**2、【xtgls】命令**
基本命令格式:
```code
xtgls depvar indepvars,options
[/code]
#如果對誤差項的處理正確,那么【xtgls】比x【tpcse】估計效果更好
**對於誤差項三大問題【xtgls】命令選項(options)的使用**
**(1)自相關問題(一階自相關)**
【xtgls】與【xtpcse】命令的選項對自相關問題的處理是相同的
a.使用選項:corr(ar1),使用的估計方法為FGLS
#誤差項存在自相關時使用該選項;當T不比n大很多時使用該選項,因為此時T可能無法提供足夠多的信息去估計每個個體的自相關系數,所以約束了每個個體的自相關系數都相等
b.使用選項:corr(psar1),使用的估計方法為FGLS。
#誤差項存在自相關時使用該選項;當T比n大很多時使用該選擇項,當T比n大很多時每個個體的自相關系數可以不同,就可以使用選項
c.使用選項:corr(independent)或corr(ind),使用的估計方法為OLS。
#誤差項不存在自相關時,使用該選項
**(2)異方差與截面相關問題**
a.使用選項:panels(iid)
#誤差項不存在異方差和截面相關,使用該選項
b.使用選項:panles(heteroskedastic)
#誤差項存在異方差但不存在截面相關問題時,使用該選項
c.使用選項:panels(correlated)#只適用於長面板數據
#誤差項存在異方差和截面相關問題時,使用該選項
選項:corr(ind)+panels(iid)等價於LSDV
**三、長面板數據分析的實例操作**
#以數據集“mus08cigar.dta”為例估計香煙需求函數,數據來源於慕課上浙江大學方紅生教授的面板數據分析與Stata應用課程中。
“mus08cigar.dta”數據集包括了美國10個州1963-1992年有關香煙消費量的相關變量。
參考上一篇文章短面板數據分析的基本程序,我們對長面板數據進行分析。
**第一步 模型設定與數據**
長面板數據不需要進行模型的選擇,我們構造一個雙向固定效應模型
![]()
其中,被解釋變量lnc為人均香煙消費量的對數,解釋變量:lnp為實際香煙價格的對數,lnpmin為相鄰州最低香煙價格的對數,lny為人均可支配收入的對數。
**在Stata軟件中對數據進行分析,執行如下步驟:**
**1、導入數據到Stata中**
在Stata的“命令窗口”中輸入命令
```code
use"數據集路徑mus08cigar.dta"
[/code]
將“traffic.dta”數據集導入到Stata中,
例如
```code
use"C:Usersmus08cigar.dta"
[/code]
將數據導入Stata后,即可在Stata的“變量窗口”中看到“mus08cigar”數據集中的各個變量的名稱及其標簽。
**2、查看數據**
在Stata的“命令窗口”輸入命令
```code
des
[/code]
和命令
```code
xtdes
[/code]
查看“mus08cigar”數據集。


從輸出結果我們可以看到:“mus08cigar”數據集包含300個觀測值,6個變量。
面板數據的截面數 ,時間數 , ,說明這是一個長面板數據集。
輸入命令
```code
xtset state year
[/code]
告訴Stata軟件,這是一個以截面變量state為州,時間變量為year的面板數據。
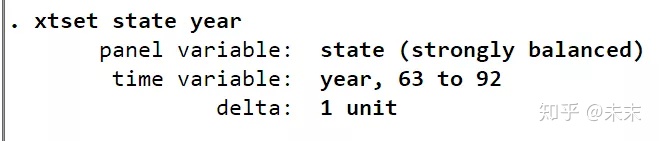
由“strongly balance”可知,這是一個平衡面板數據。
至此,我們可以知道,“mus08cigar”數據集是一個10個州,1963-1992年的長面板數據集且為平衡面板數據集。
**第二步 描述性統計作圖**
**1、描述性統計**
**使用命令【sum 關鍵變量】可以得到關鍵變量的描述性統計表。**
在Stata中輸入命令
```code
sum lnc lnp lnpmin lny
[/code]
得到解釋變量與被解釋變量的觀測值、均值、標准差、最小值和最大值。
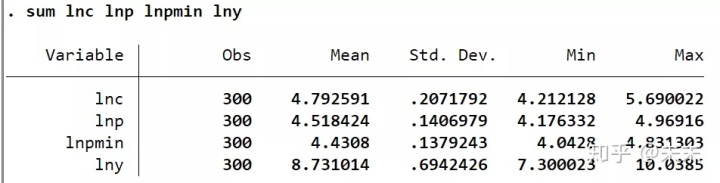
**2、繪制散點圖及回歸直線**
**在回歸之前,我們先畫出核心變量lnp與被解釋變量lnc的散點圖及回歸直線,來預先觀測一下核心變量與被解釋變量之間是否存在理論上預期的負相關系。**
使用命令
```code
twoway(scatter lnc lnp)(lfit lnc lnp)
[/code]
畫出核心變量“lnp”與被解釋變量“lnc”的散點圖及回歸直線。

由結果可知,lnp與lnc之間是負相關系的,與理論預期一致。
接下來,我們做出相鄰州的香煙價格的對數與被解釋變量的散點圖及回歸直線,看一下核心變量lnpmin與被解釋變量lnc之間是否存在理論上預期的正相關系。使用命令
```code
twoway(scatter lnc lnpmin)(lfit lnc lnpmin)
[/code]
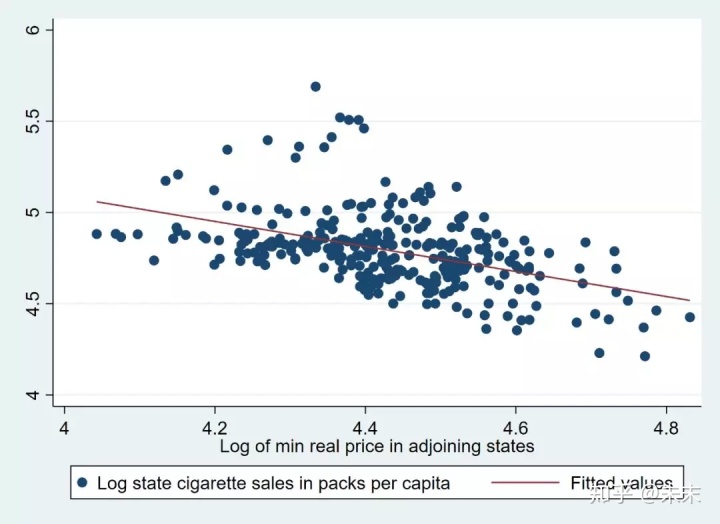
由結果可知,相鄰州的香煙價格的對數lnpmin與被解釋變量lnc之間是正相關系的,這與我們的理論預期並不符合。
不過,因為我們並沒有控制其他的影響因素,所以這個結果並不是完全正確的,在之后的操作中,我們可以使用命令【avplot】繪制變量之間的偏相關圖。
**3、繪制核心變量的時間序列圖**
使用命令
```code
xtline lnc
[/code]
做出核心變量人均香煙消費的對數lnc在各個州的時間序列圖,以研究分析人均香煙消費的對數lnc在每個州中的變動趨勢。
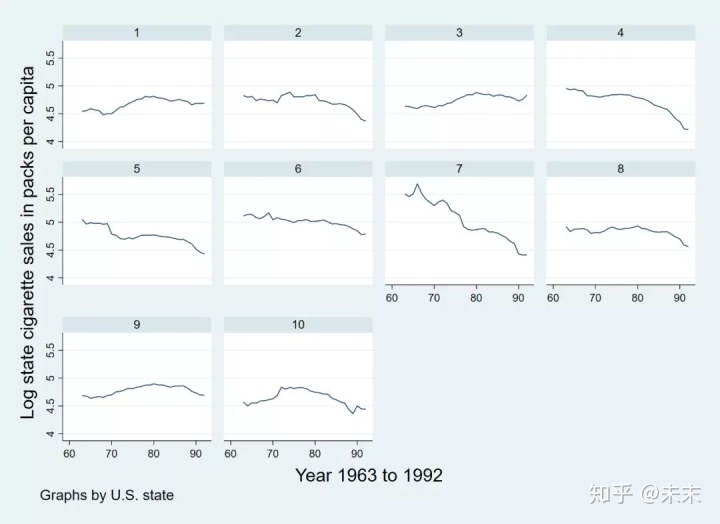
觀察lnc在各個州的時序圖,我們可以發現,1980年之后,所有州的人均香煙消費率基本都呈現出下降趨勢。
使用命令
```code
xtline lnp
[/code]
做出美國10個州1963-1992年實際香煙價格對數的時間序列圖。
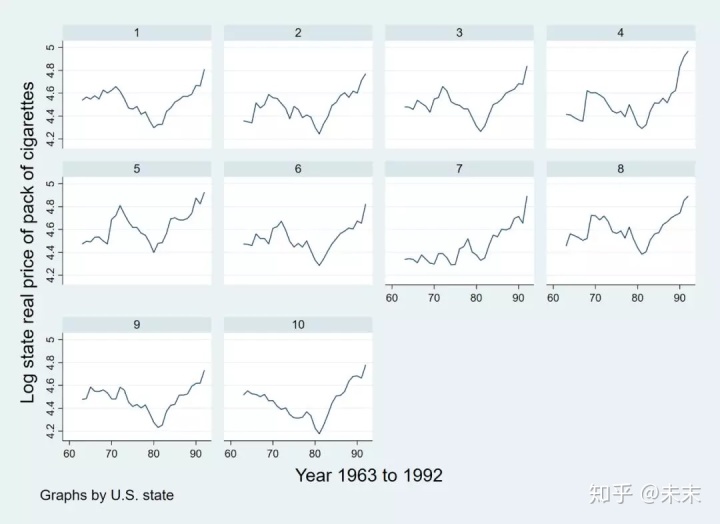
觀察發現:1980年之后,所有州的香煙價格基本都呈現了上升的趨勢。
**第三步 模型估計**
**首先** ,我們先假定不存在自相關、異方差和截面相關這三大問題,使用LSDV估計雙向固定效應模型。
依次進行如下操作:
使用命令
```code
tab state,gen(state)
[/code]
生成州虛擬變量;
使用命令
```code
gen t=year-62
[/code]
生成時間趨勢變量;
輸入命令
```code
reg lnc lnp lnpmin lny state2-state10 t
[/code]
進行LSDV估計;
輸入命令
```code
est store ols
[/code]
保存結果。
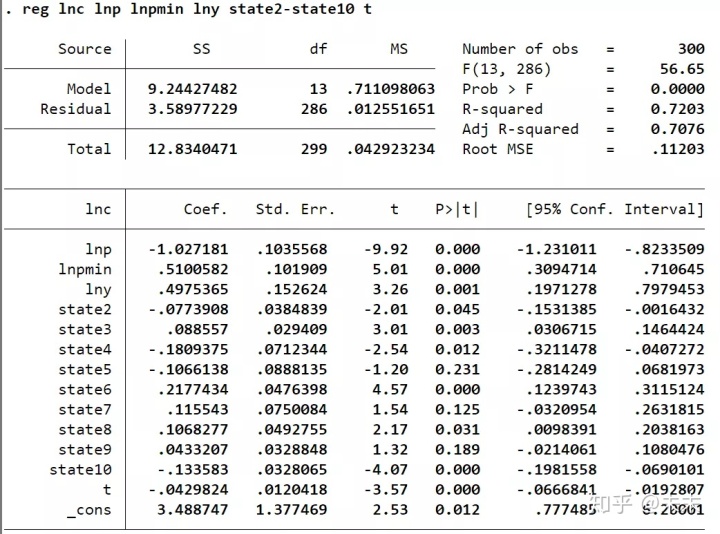
然后,我們輸入命令
```code
avplot lnp
[/code]
查看核心解釋變量lnp與被解釋變量lnc的偏相關圖。
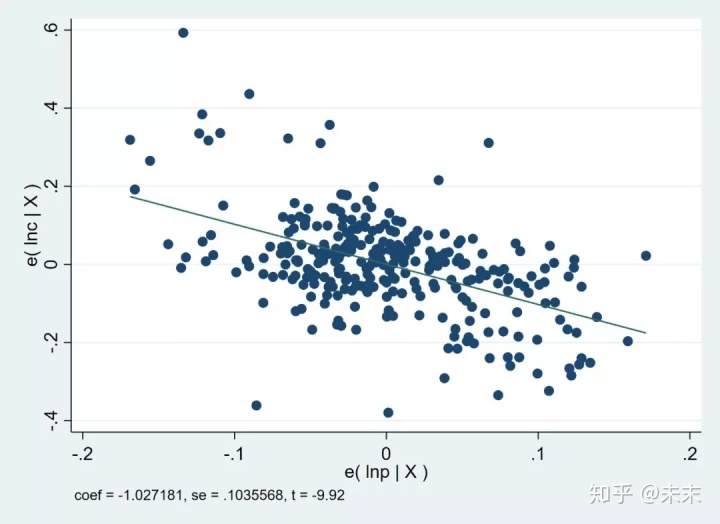
可以發現,兩者之間明顯呈現負相關關系。
**接下來** ,我們檢驗誤差項是否存在自相關、異方差和截面相關的問題。
**1、自相關的檢驗**
使用命令
```code
xtserial lnc lnp lnpmin lny state2-state10 t
[/code]
檢驗誤差項的自相關問題。

由檢驗結果可知,P值為0,所以拒絕一階自相關不存在的原假設,表明存在自相關問題。
**2、異方差的檢驗**
使用命令【xttest3】對誤差項的異方差問題進行檢驗。
#【xttest3】只能在【xtreg,fe】和【xtgls】命令之后使用;
#第一次使用【xttest3】的同學,需要使用命令【ssc install xttest3】進行安裝
在Stata中輸入命令
```code
quietly xtreg lnc lnp lnpmin lny t,fe
[/code]
然后輸入命令
```code
xttest3
[/code]
(也可以輸入命令【quietly xtgls lnc lnp lnpmin lny state2-state10 t】和【xttest3】)

由檢驗結果可知,P值為0,所以拒絕原假設,認為誤差項存在異方差問題。
**3、截面相關的檢驗**
使用命令【xttest2】對誤差項的截面相關問題進行檢驗。
#【xttest2】只能在【xtreg,fe】、【xtgls】或【ivreg2】之后使用,只適用於長面板數據;
#第一次使用【xttest2】的同學,需要使用命令【ssc install xttest2】進行安裝
在Stata中輸入命令
```code
quietly xtreg lnc lnp lnpmin lny t,fe
[/code]
然后輸入命令
```code
xttest2
[/code]
(也可以輸入命令【quietly xtgls lnc lnp lnpmin lny state2-state10 t】和【xttest2】)
當然,因為我們上一步進行了誤差項異方差問題的檢驗,所以這一步我們可以直接輸入命令
```code
xttest2
[/code]

可以看到,檢驗結果的P值為0,所以拒絕原假設,認為誤差項存在截面相關的問題。
綜上,通過檢驗,我們發現模型誤差項存在自相關、異方差和截面相關的問題。
**第四步 報告計量結果**
通過第三步對模型誤差項的檢驗,我們知道模型的誤差項存在自相關、異方差和截面相關的問題,所以,我們需要對誤差項的自相關、異方差和截面相關問題進行處理並報告計量結果。
對【xtpcse】、【xtgls】和【xtscc】三個命令的結果分別進行報告。
**依次輸入命令:**
```code
xtpcse lnc lnp lnpmin lny state2-state10 t,corr(psar1)
est store xtpcse
xtgls lnc lnp lnpmin lny state2-state10 t,corr(psar1) panels(correlated)
est store xtgls
xtscc lnc lnp lnpmin lny state2-state10 t
est store xtscc
[/code]
最后通過【esttab】命令將所有的存儲結果放在一起進行比較。
輸入命令
```code
esttab ols xtpcse xtgls xtscc,b(%9.2f)p mtitle(ols xtpcse xtgls xtscc)obslast star(* 0.1 ** 0.05 *** 0.01)compress nogap k(lnp lnpmin lny t)
[/code]
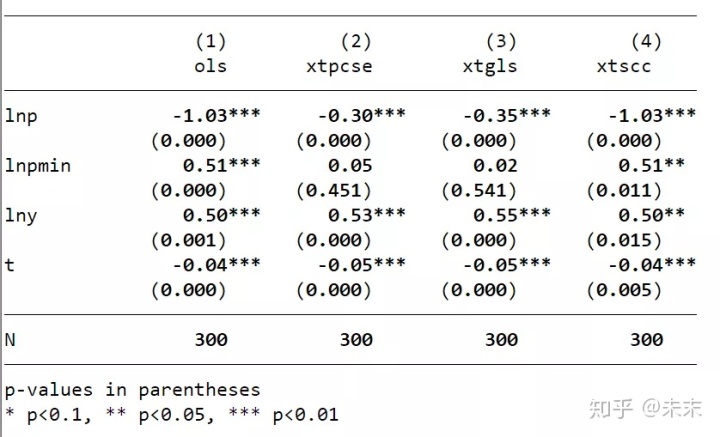
輸出的表格中,(1)的結果是不對誤差項做任何處理的結果,(2)、(3)、(4)是分別使用三種命令並對誤差項的三大問題進行處理的結果。
