快速莫比烏斯/沃爾什變換 (FMT/FWT)

更新了 FWT-xor 地方關於底數選取的討論。

\[c_x=\sum_{i\oplus j=x}a_ib_j \]

當 \(\oplus\) 為 \(+\) 時，這個就是多項式乘法。

FMT/FWT 則是處理 \(\oplus\) 為 \(\rm{or,and,xor}\) 時的問題。

快速莫比烏斯變換和莫比烏斯函數/反演並無關系。

FMT 處理 \(\rm{or/and}\) 時的問題，可以看作是集合的 交/並 來看。

FWT 處理 \(\rm{xor}\) 時的問題。但是有時把 FMT 和 FWT 統稱為 FWT。

下面的講解可能都會帶一點集合的味道，但是我不擅長這玩意，有描述不對的地方麻煩指出。

如果我的描述讓你感到了疑惑，可以訪問 這篇博文 ，也許他的講解會讓你更理解一些。

計算

1.\(\rm or\)(並)

\[c_x=\sum_{i∪j=x}a_ib_j \]

考慮對一個序列 \(\text F\) 進行莫比烏斯變換，得到 \(\rm{FMT(F)}\) ,\(\rm F\) 序列的第 \(\rm x\) 項記為 \(\rm{F_x}\)。

如果我們有 \(\rm{FMT(c)_n=FMT(a)_n*FMT(b)_n}\) ，並且可以 \(\rm{FMT(F)→F}\) ，那就可以解決這個問題了。

我們考慮讓 \(\rm{FMT(F)_n=\sum_{i\subseteq n}F_i}\)。

\[\begin{aligned} &\rm{FMT(a)_n*FMT(b)_n}\\ &\rm{=\sum_{i\subseteq n}a_i\sum_{j\subseteq n}b_j}\\ &\rm{=\sum_{k\subseteq n}\sum_{i∪j=k}a_ib_j}\\ &\rm{=FMT(c)_n} \end{aligned} \]

交換枚舉的那個意義是先枚舉 \(\rm{k=i∪j}\)，然后再枚舉合法的 \(\rm{i,j}\) ，這樣和之前的枚舉是等價的。

問題就轉化為了如何快速變換了，也就是如何快速求子集和。

那我們考慮一種增量構造的方法。

令 \(\rm{T_n}\) 表示 \(\rm{FMT(F)_n}\) 。

新加入第 \(i\) 個點。

如果不選，那么集合是 不選 \(i\) 的，答案不會變。

如果選了，那么集合是 選擇 \(i\) 了的， 不選 \(i\) 時的集合 會成為新的集合的子集，那答案也要對應加上去。

也就是用 選 \(i\) 的答案加上 不選 \(i\) 的答案，合並即可。

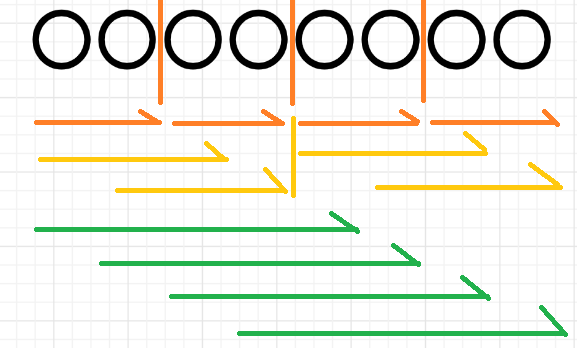
如圖，這個過程可以分成 \(\log\) 層來做，箭頭就是累加，時間復雜度 \(\mathcal O(n\log n)\) 。

考慮反過來的過程，我們就是要通過子集和反推原來的數列，那就把加進來的減回去就好了。

void FMT_or(int *f,int n,int op){//op=1 FMT op=-1 IFMT
	for(int i=1;i<n;i<<=1)
		for(int o=i<<1,j=0;j<n;j+=o)
			for(int k=0;k<i;k++)
				(f[i+j+k]+=f[j+k]*op+p)%=p;
}

---

2.\(\rm{and}\)(交)

\[c_x=\sum_{i∩j=x}a_ib_j \]

和 \(\rm{or}\) 相似地，我們考慮 \(\rm{FMT(F)_n}=\sum_{n\subseteq i}F_i\)。

\[\begin{aligned} &\rm{FMT(a)_n*FMT(b)_n}\\ &\rm{=\sum_{n\subseteq i}\sum_{n\subseteq j}a_ib_j}\\ &\rm{=\sum_{n\subseteq x}\sum_{i∩j=x}a_ib_j}\\ &\rm{=FMT(c)_n} \end{aligned} \]

最后的改變枚舉對象和上面也是類似的，可以不重不漏的枚舉到所有的情況，只是換了個形式和 FMT(c) 重合。

也是相似地，我們考慮增量構造的方法求 \(\rm{\sum_{n\subseteq i}F_i}\)。

新加入一個元素 \(i\) 。

如果 選 \(i\) ，對應的集合和答案都不會變。

如果 不選 \(i\) ，集合在 \(i\) 這一位就對應 0 ，也就是縮小了，會成為 選 \(i\) 對應集合的子集。

由於求和方式的不同，和上面相反，這里需要的是用 不選 \(i\) 的答案加上 選 \(i\) 的答案。代碼類似。

反過來的話是類似的，逐步減去即可。

void FMT_and(int *f,int n,int op){//op=1 FMT op=-1 IFMT
	for(int i=1;i<n;i<<=1)
		for(int o=i<<1,j=0;j<n;j+=o)
			for(int k=0;k<i;k++)
				(f[j+k]+=f[i+j+k]*op+p)%=p;
}

---

3.\(\rm{xor}\)

\[c_x=\sum_{i\ xor\ j=x}a_ib_j \]

這里的 \(\rm{FWT(F)}\) 不太好構造，稍微推導一下這個是怎么來的。

設 \(\rm{FWT(F)_n=\sum_{i=0}^n}g(n,i)F_i\) ，這么設的原因是因為 \(\rm{FWT(F)_n}\) 的第 \(i\) 項的系數肯定只和 \(n,i\) 線性相關，因為我們沒有乘除操作。

然后帶入 \(\rm{FWT(c)_n=FWT(a)_n*FWT(b)_n}\) 中。

\[\begin{aligned} &\rm{\sum_{i=0}^ng(n,i)c_i=\sum_{j=0}^ng(n,j)a_j\sum_{k=0}^ng(n,k)b_k}\\ &\rm{\sum_{i=0}^ng(n,i)\sum_{j\ xor\ k=i}a_jb_k=\sum_{j=0}^ng(n,j)a_j\sum_{k=0}^ng(n,k)b_k}\\ &\rm{\sum_{j=0}^n\sum_{k=0}^ng(n,j\ xor \ k)a_jb_k=\sum_{j=0}^n\sum_{k=0}^ng(n,j)g(n,k)a_jb_k}\\ \end{aligned} \]

不難發現， \(\rm{g(n,j\ xor\ k)=g(n,j)*g(n,k)}\)，那接下來要思考的就是啥樣的東西會把 \(\rm{j,k}\) 和 \(\rm{j\ xor\ k}\) 聯系起來。

雖然確實難想到，但是 \(\rm{popcount(a)+popcount(b)\equiv popcount(a\ xor\ b)\pmod 2}\) 。

所以就有 \(\rm{g(n,i)=(-1)^{|i∩n|}}\) 。這里把 \(i,n\) 看做集合，實際就是取出了 \(i\) 中 \(n\) 是 1 的位數。

那么就可以 \(\rm{FWT(F)_x=\sum_{i=0}^n(-1)^{|i∩x|}F_i}\)。

按道理，這里的 -1 是可以換成任意數的，但是稍微把 0,1 這種數帶進去就知道有問題。問題出在哪呢？

我們定義 g 的時候就說了，它和 n,i 線性相關，但是當底數是 0,1 的時候，它似乎和 n,i 不太相關。0 只有它的 0 次冪可以定義為 1，但計算起來就會出問題。1 的任何整數次冪都是 1，所以完全和指數沒有關系。

那如果放 2 進去當底數呢，它不滿足 \(\rm{2^i}= 2^{i\ mod\ 2}\) ，所以不太行。

綜合下來，只有 -1 作為底數，便於計算，也便於進行逆運算。

容易證明 \(\rm{g(n,i)*g(n,j)=(-1)^{|i∩n|+|j∩n|}=(-1)^{|(i\ xor\ j)∩n|}=g(n,i\ xor\ j)}\) 。

依然仿造 \(\rm{FMT}\) 考慮增量構造方法。

新加入一位 \(i\) ，分選或者不選考慮。

選。和選的集合取並，大小不變。和不選的集合取並，大小 -1 。

不選。和選的集合取並，大小不變。和不選的集合取並，大小也不變。

所以 \(i\) 這一位如果 選 ，那會累加到原來的 選 上，累減到原來的 不選 上。

如果 不選，那會累加到原來的選和不選上。

也就是 int x=f[j+k],y=f[i+j+k];f[i+j+k]=x-y,f[j+k]=x+y ，就有 \(\rm{FFT}\) 那種感覺了。

逆變換的話是反過來，移一下項，f[i+j+k]=(x-y)/2,f[j+k]=(x+y)/2。

於是就做完了。

void FWT_xor(int *f,int n,int op){//op=1 FWT op=-1 IFWT
	for(int i=1;i<n;i<<=1)
		for(int o=i<<1,j=0;j<n;j+=o)
			for(int k=0;k<i;k++){
				int x=f[j+k],y=f[i+j+k];
				f[j+k]=(x+y)%p,f[i+j+k]=(x-y+p)%p;
				if(op==-1)(f[j+k]*=inv2)%=p,(f[i+j+k]*=inv2)%=p;
			}
}

---

感謝閱讀。