第4章 李群李代數

一、概述

1. 李群和李代數的核心思想

   1. 可以理解為專門用於矩陣旋轉的東西，符合封結幺逆法則；

   2. 李群可以理解為旋轉矩陣，李代數可以理解為旋轉向量；

   3. 李群是連續群，李代數可以表出李群的導數，所以李代數表示的是李群的局部性質；

   4. 進而我們可以理解為：旋轉向量表達了旋轉矩陣的局部（旋轉發生那一瞬間的領域內）性質；

   5. 由拉格朗日中值定理可知：導數控制函數。李代數控制李群，\(\phi\)控制\(R\)；^【1】

      也就是說想要估計出函數值，我們可以研究該函數的導數，用來描述某個點領域內性質。故而我們需要建立對李群的求導模型，通過分析導數的性質來估計出相機在這一時刻（領域內）的位姿。

      但是我們知道群是指只有一個運算的集合（我們選擇矩陣乘法），所以李群不對加法封閉^【2】，但是我們知道李代數是建立在向量空間上的，支持加法運算。所以我們需要一種讓李群映射到李代數的機制，然后通過對李代數求導，求出李群的導數。不過，對李代數求導后的結果非常復雜，所以我們需要尋找另外一種求導方式^【3】，這就是我們接下來所要介紹的內容。

      【注】

      ^【1】：某個名牌大學考研的復試題——你知道導數的作用是什么嗎？

      ^【2】：李群也是一種群。甭跟我扯什么鱷魚不是魚、日本人不是人。

      ^【3】：對誰求導不重要，因為我們總可以通過這個導數控制相同的函數。

2. 李群的兩種求導模型（都是映射到了李代數空間）

   1. BCH公式線性化（將李群的變化與李代數的變化聯系起來）；

   2. 對李代數求導的求導模型；（復雜）

      1. 需要求出左右雅可比矩陣的逆；

   3. 對微擾動求導的擾動模型；（精簡）

      1. 不需要求出左右雅可比矩陣的逆；

3. 這兩種求導模型都是會有誤差存在的

4. 李群和李代數的基礎符號

   1. 特殊正交群\(SO(3)\)，特殊歐式群\(SE(3)\)；

   2. 特殊正交群上的李代數\(\mathfrak{so}(3)\)，這里我們具象化為三維\(\phi\)向量或者反對稱陣\(\widehat{\phi}\)；

      

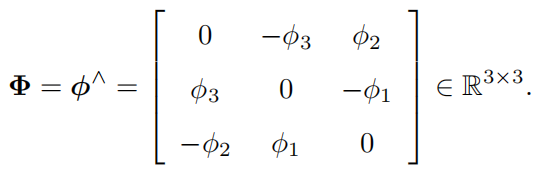
   3. 特殊歐式群上的李代數\(\mathfrak{se}(3)\)，這里我們具象化為六維\(\xi\)向量或者四維方陣\(\widehat{\xi}\)；

      

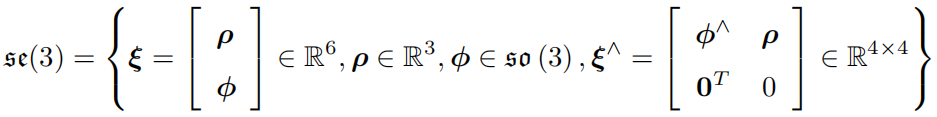
      \(\rho\)表示三維空間中的平移，\(\phi\)表示三維空間中的旋轉。

   4. 反對稱矩陣與相應的三維向量：\(\wedge\)和\(\vee\)；

      

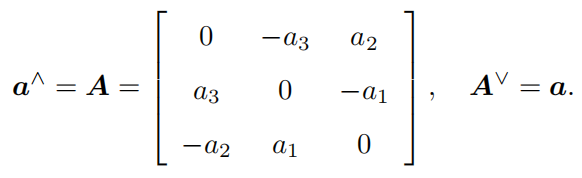
   5. 向量\(\overrightarrow{a}\)和\(\overrightarrow{\omega}\)都表示旋轉向量的單位方向向量，\(\theta\)表示旋轉角，\(\overrightarrow{\phi}\)表示旋轉向量，\(R\)表示旋轉矩陣；

   6. 有時為了格式不顯得過於復雜，會省略掉向量標識\(\overrightarrow{}\)；

5. Sophus庫的使用

   1. \(SO(3)\)和\(\mathfrak{so}(3)\)

      // 構造旋轉向量、旋轉矩陣、四元數
      Eigen::AngleAxisd RV = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1));
      Eigen::Matrix3d RM = RV.toRotationMatrix();
      Eigen::Quaterniond QD(RM);
      // 通過上述旋轉表述構造李群
      Sophus::SO3d SO3_RM(RM);
      Sophus::SO3d SO3_QD(QD);
      // 輸出SO(3)時，以so(3)形式輸出
      cout << "SO(3) from matrix    :" << SO3_RM.log().transpose() << endl;
      cout << "SO(3) from quaternion:" << SO3_QD.log().transpose() << endl;
      
      // 使用對數映射獲得它的李代數
      Eigen::Vector3d so3 = SO3_RM.log();
      cout << "so3 = " << so3.transpose() << endl;
      // hat為向量到反對稱矩陣
      cout << "so3 hat=" << endl << Sophus::SO3d::hat(so3) << endl;
      // vee為反對稱矩陣到向量
      cout << "so3 hat vee= " << Sophus::SO3d::vee(Sophus::SO3d::hat(so3)).transpose() << endl; 
      
      // 增量擾動模型的更新
      Eigen::Vector3d update_so3(1e-4, 0, 0);
      Sophus::SO3d SO3_updated = Sophus::SO3d::exp(update_so3) * SO3_RM;
      cout << "SO3 updated = " << endl << SO3_updated.matrix() << endl;
      

   2. \(SE(3)\)和\(\mathfrak{se}(3)\)

      // 構造旋轉向量、旋轉矩陣、四元數
      Eigen::AngleAxisd RV = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1));
      Eigen::Matrix3d RM = RV.toRotationMatrix();
      Eigen::Quaterniond QD(RM);
      // 通過上述旋轉表述構造李群
      Sophus::SO3d SO3_RM(RM);
      Sophus::SO3d SO3_QD(QD);
      // 對SE(3)操作大同小異
      Eigen::Vector3d t(1,0,0);           // 沿X軸平移1
      Sophus::SE3d SE3_RMt(RM, t);           // 從R,t構造SE(3)
      Sophus::SE3d SE3_QDt(QD, t);            // 從q,t構造SE(3)
      cout << "SE3 from RM,t = " << SE3_RMt.log().transpose() << endl;
      cout << "SE3 from QD,t = " << SE3_QDt.log().transpose() << endl;
      // 李代數se(3) 是一個六維向量，方便起見先typedef一下
      typedef Eigen::Matrix<double,6,1> Vector6d;
      Vector6d se3 = SE3_RMt.log();
      cout << "se3 = " << se3.transpose() << endl;
      // 觀察輸出，會發現在Sophus中，se(3)的平移在前，旋轉在后.
      // 同樣的，有hat和vee兩個算符
      cout << "se3 hat = " << endl << Sophus::SE3d::hat(se3) << endl;
      cout << "se3 hat vee = " << Sophus::SE3d::vee(Sophus::SE3d::hat(se3)).transpose() << endl;
      
      // 最后，演示一下更新
      Vector6d update_se3; //更新量
      update_se3.setZero();
      update_se3(0,0) = 1e-4;
      Sophus::SE3d SE3_updated = Sophus::SE3d::exp(update_se3) * SE3_RMt;
      cout << "SE3 updated = " << endl << SE3_updated.matrix() << endl;
      

二、詳述

1. 從物理角度引出

   

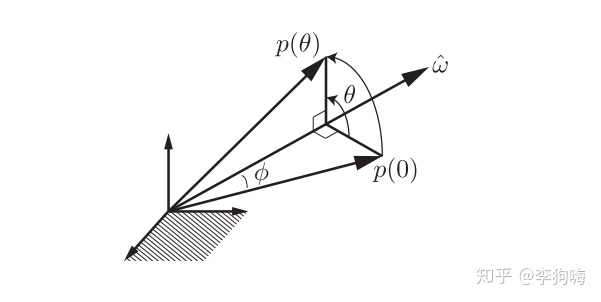
   假設有一個三維的向量\(\overrightarrow{p(0)}\)繞着旋轉軸\(\overrightarrow{\omega}\)旋轉了\(\theta\)角度（旋轉所需時間為\(t\)）到達了\(\overrightarrow{p(t)}\)處，由小學二年級就學過的知識知道：\(\overrightarrow{速度}=\overrightarrow{角速度}\times\overrightarrow{（旋轉中心，旋轉點）}\)。

   我們不妨設\(\overrightarrow{p(t)}\)領域處的速度為\(\overset{\bullet}{\overrightarrow{p(t)}}\)，故而有公式：\(\overset{\bullet}{\overrightarrow{p(t)}}=\overrightarrow{\omega}\times\overrightarrow{p(t)}=\widehat{\overrightarrow{\omega}}\cdot\overrightarrow{p(t)}\)^【1】。這其實是一個關於\(\overrightarrow{p(t)}\)的微分方程^【2】，並且當\(\overrightarrow{\omega}\)是單位向量，即值為\(1\ \mathbf{rad/s}\)時有\(\theta=t\)，所以不難解出：

   \[\overrightarrow{p(t)}=e^{\widehat{\overrightarrow{\omega}}\cdot{t}}\cdot{\overrightarrow{p(0)}}，由此我們不難看出\overrightarrow{p(0)}到\overrightarrow{p(t)}的旋轉矩陣：R(t)=e^{\widehat{\overrightarrow{\omega}}\cdot{t}}=e^{\widehat{\overrightarrow{\omega}}\cdot{\theta}}=e^{\widehat{\overrightarrow{\phi}}}； \]

   所以我們便可的出結論：旋轉向量和旋轉矩陣存在指數映射關系，且多對一對應（旋轉周期性）。

   為了統一化表述，我們稱旋轉矩陣為李群\(SO(3)\)，旋轉向量為\(\mathfrak{so}(3)\)，它們之間有指數映射關系。

   注^【1】：如果這個時候你仍然以向量為參考，那可能有點兒不太好理解，但要是將視線移至坐標系身上的化，也就是說是坐標系在旋轉，那就不難理解：旋轉軸是\(\overrightarrow{\omega}\)，旋轉中心是原點。

   注^【2】：標量微分方程與矢量微分方程如下所示：

   \[\begin{aligned} &\overset{\bullet}{x(t)}=a\cdot{x(t)}，且x(0)=x_0&\Longrightarrow&\quad x(t)=e^{at}\cdot{x_0}； \\\\ &\overset{\bullet}{X(t)}=A\cdot{X(t)}，且X(0)=X_0&\Longrightarrow&\quad X(t)=e^{At}\cdot{X_0}； \end{aligned} \]

2. 指數與對數映射

   1. 矩陣的泰勒展開

      \[e^{\widehat{\overrightarrow{\omega}}\cdot{\theta}}=\sum_{n=0}^{\infty}{\frac{1}{n!}(\overrightarrow{\omega}}{\theta})^n=\sum_{n=0}^{\infty}{\frac{{\theta}^n}{n!}(\overrightarrow{\omega}})^n \]

   2. 反對稱陣的性質

      \[\begin{cases} \widehat{\overrightarrow{\omega}}\cdot{\widehat{\overrightarrow{\omega}}}=\overrightarrow{\omega}\cdot{\overrightarrow{\omega}^T}-I \\\\ \widehat{\overrightarrow{\omega}}\cdot{\widehat{\overrightarrow{\omega}}\cdot{\widehat{\overrightarrow{\omega}}}}=-{\widehat{\overrightarrow{\omega}}} \end{cases} \]

   3. 指數映射的推導

      1. \(\mathfrak{so}(3) \Longrightarrow SO(3)\)的推導

         

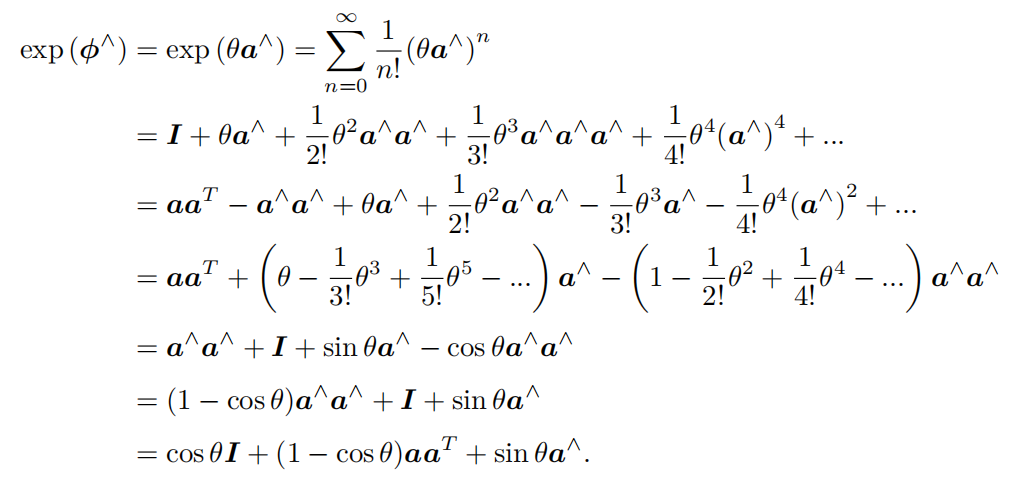
      2. \(\mathfrak{se}(3) \Longrightarrow SE(3)\)的推導

         

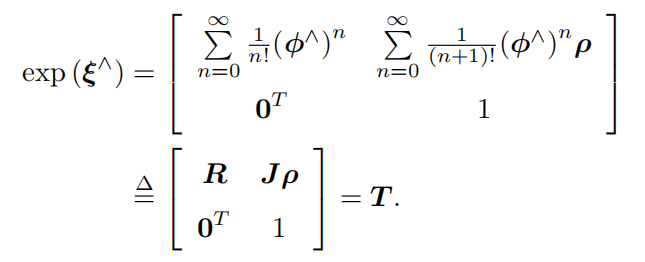
         如果你嘗試這將上面的\(J\)泰勒展開，將會得到下面的公式（請務必有印象！）：

         

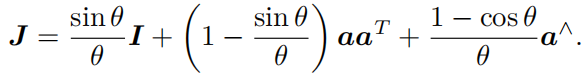
         而旋轉矩陣\(R\)通過上述的\(\mathfrak{so}(3) \Longrightarrow SO(3)\)已經給出。

   4. 對數映射的推導

      1. \(SO(3)\Longrightarrow\mathfrak{so}(3)\)的推導

         

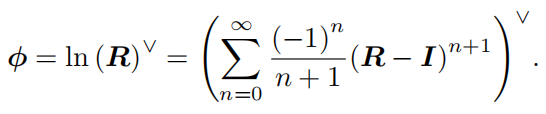
         只有傘兵才會這樣推導，之前在《矩陣旋轉》中就提到了如何從旋轉矩陣到旋轉向量，我們只需知道旋轉矩陣的跡\(\mathbf{tr}(R)\)解出\(\theta\)，並解出特征值為1的特征向量並歸一化得到\(\omega\)。

      2. \(SE(3)\Longrightarrow\mathfrak{se}(3)\)的推導

         由上述\(SO(3)\Longrightarrow\mathfrak{so}(3)\)我們可以通過旋轉\(R\)求出旋轉向量\(\phi\)，而\(\overrightarrow{t}=J\rho\)得\(\rho=J^{-1}\overrightarrow{t}\)；

3. 李群和李代數的對應關系

   

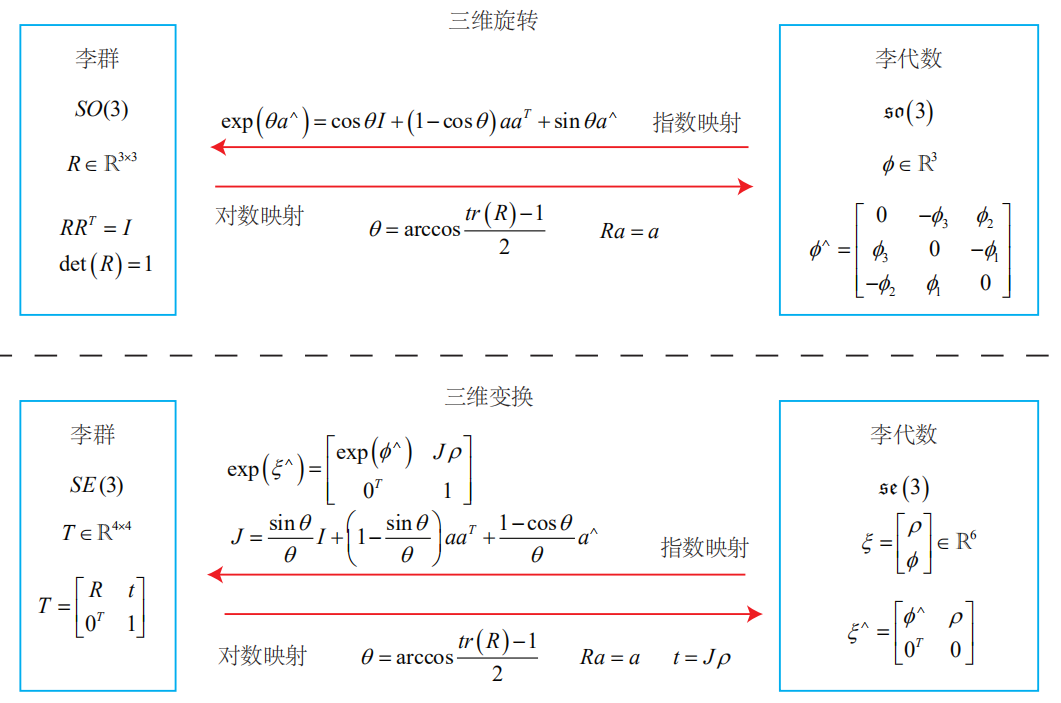
三、李代數的求導和擾動模型（左乘）

1. BCH公式和它的線性近似式

   1. BCH公式的引出

      在高等數學中，我們研究的大部分問題都是標量（也就是純數值）的問題，所以一定滿足下面恆等式

      \[\ln(e^A\cdot{e^B})\equiv{A+B}\\ \ln(e^\widehat{a}\cdot{e^\widehat{b}})\equiv{(a+b)^{\wedge}} \]

      但是很不幸的是，我們在SLAM中研究的是向量（或者說矩陣），反正不是標量，所以不能滿足上式。這個東西在向量空間中的計算很是復雜，但是這個世界上總有些神仙搗鼓這種玩意兒，比如Baker-Campbell-Hausdorff這哥仨就為這個東西的計算給出了BCH公式。

   2. BCH的完全展開

      \[\ln(e^A\cdot{e^B})=A+B+\frac{1}{2}[A，B]+\frac{1}{12}[A，[A，B]]-\frac{1}{12}[B，[A，B]]+\cdots \]

      其中\([，]\)表示李括號運算。也就是說，這天底下就沒有干干凈凈的事，矩陣指數之積會產生一堆李括號余項。

   3. BCH線性近似式

      但凡事不能說得太絕對。雖說這BCH公式的完全展開很復雜，但是后面那一堆東西叫做余項啊！也就是說，當\(\overrightarrow{\phi_1}\)或者\(\overrightarrow{\phi_2}\)是小量的時候，它們的高階就是高階無窮小量了，可以被忽略的！這個時候BCH公式就變得非常‘和藹可親’了（近乎線性的表達）

      \[\ln(e^{\widehat{\phi_1}}\cdot{e^{\widehat{\phi_2}}})^{\vee}\approx \begin{cases} 左乘模型：J_l^{-1}(\phi_2)\cdot{\phi_1}+\phi_2，當\phi_1為小量時； \\\\ 右乘模型：J_r^{-1}(\phi_1)\cdot{\phi_2}+\phi_1，當\phi_2為小量時； \end{cases} \]

      至此，我們將李群\(SO(3)\)（旋轉矩陣）和李代數\(\mathfrak{so}(3)\)（旋轉向量）線性化了。

      可以理解為：旋轉矩陣\(R_2\)左乘了一個微小旋轉矩陣\(R_1\)，相當於旋轉向量\(\phi_2\)加上了經過左雅可比逆\(J_l^{-1}(\phi_2)\)旋轉后的旋轉向量\(\phi_1\)。右乘微小矩陣\(R_2\)亦可模仿理解。

   4. BCH公式的意義

      1. 李群 \(\Longrightarrow\) 李代數

         \[\begin{cases} 左乘模型：e^{\widehat{\Delta\phi}}\cdot{e^{\widehat{\phi}}}=e^{【J_l^{-1}(\phi)\cdot{\Delta\phi}+\phi】^{\wedge}} \\\\ 右乘模型：e^{\widehat{\phi}}\cdot{e^{\widehat{\Delta\phi}}}=e^{【J_r^{-1}(\phi)\cdot{\Delta\phi}+\phi】^{\wedge}} \end{cases} \]

      2. 李代數 \(\Longrightarrow\) 李群

         \[e^{【\phi+\Delta\phi】^{\wedge}}= \begin{cases} 左乘模型：e^{【\phi+J_l^{-1}(\phi)\cdot{J_l(\phi){\Delta\phi}}】^{\wedge}} =e^{【J_l(\phi){\Delta\phi}】^{\wedge}}\cdot{e^{\widehat{\phi}}} \\\\ 右乘模型：e^{【\phi+J_r^{-1}(\phi)\cdot{J_r(\phi){\Delta\phi}}】^{\wedge}} =e^{\widehat{\phi}}\cdot{e^{【J_r(\phi){\Delta\phi}】^{\wedge}}} \end{cases} \]

      3. 李代數解決李群的求導問題

         李群沒有加法，所以很難用導數的一般定義去求導數，但是李代數允許加法^【1】。所以如果想要對李群求導數，我們可以運用指數映射法則和BCH公式轉換成李代數，然后用定義區求導數（乘除變加減）。

         【注】^【1】：李群是群，不對加法封閉。李代數定義在向量空間，對加法封閉。

   5. 左右雅可比矩陣的計算

      

   6. 在\(SE(3)\)上同樣有線性化公式

      

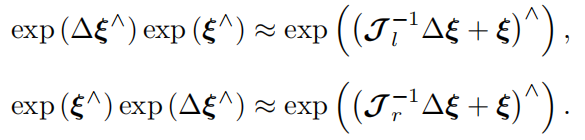
      其中的左右雅可比矩陣表述十分復雜，並且我們以后不會用到它來計算，所以就將其視為一個常數符號。

2. 李代數\(SO(3)\)的求導

   假設一個向量\(\overrightarrow{p}\)經過了旋轉矩陣\(R\)的作用，旋轉矩陣對應的李代數（旋轉向量）為\(\phi\)；

   1. 對李代數求導（求導模型）

      \[公式 控制\begin{aligned} &\frac{\part{(Rp)}}{\part{\phi}} = \frac{\part{(Rp)}}{\part{\phi}} = \frac{\part{(e^{\widehat{\phi}}\cdot{p})}}{\part{\phi}} \\\\=&\underset{\Delta\phi\rightarrow0}{\lim} \frac{(e^{(\phi+\Delta\phi)^{\wedge}}-e^{\phi^{\wedge}})\cdot{p}}{\Delta\phi} ，（利用左乘模型得） \\\\=&\underset{\Delta\phi\rightarrow0}{\lim} \frac{(e^{【J_l(\phi){\Delta\phi}】^{\wedge}}\cdot{e^{\widehat{\phi}}}-e^{\phi^{\wedge}})\cdot{p}}{\Delta\phi} ，（利用矩陣的等價無窮小替換） \\\\=&\underset{\Delta\phi\rightarrow0}{\lim} \frac{【J_l(\phi){\Delta\phi}】^{\wedge}\cdot{e^{\widehat{\phi}}p}}{\Delta\phi} ，（將反對陳矩陣\wedge符號換成叉積\times，再交換順序） \\\\=& -【e^{\widehat{\phi}}p】^{\wedge}J_l(\phi) = -(Rp)^{\wedge}J_l{(\phi)} \end{aligned} \]

   2. 對微擾動求導（擾動模型）

      假設這個時候對\(R\)有一個作用在左邊的微小擾動\(\Delta R\)，對應的李代數為\(\psi\)。（左右干擾模型不同！！）

      \[\begin{aligned} &\frac{\part{(Rp)}}{\part{\psi}} = \frac{\part{(Rp)}}{\part{\psi}} = \frac{\part{(e^{\widehat{\phi}}\cdot{p})}}{\part{\psi}} \\\\=&\underset{\Delta\phi\rightarrow0}{\lim} \frac{(e^{\psi^{\wedge}}e^{\phi^{\wedge}}-e^{\phi^{\wedge}})\cdot{p}}{\psi} ，（利用矩陣的等價無窮小替換） \\\\=&\underset{\Delta\phi\rightarrow0}{\lim} \frac{\psi^{\wedge}\cdot{e^{\phi^{\wedge}}p}}{\psi} ，（將反對陳矩陣\wedge符號換成叉積\times，再交換順序） \\\\=& -【e^{\widehat{\phi}}p】^{\wedge}=-(Rp)^{\wedge} \end{aligned} \]

3. 李代數\(SE(3)\)的求導

   

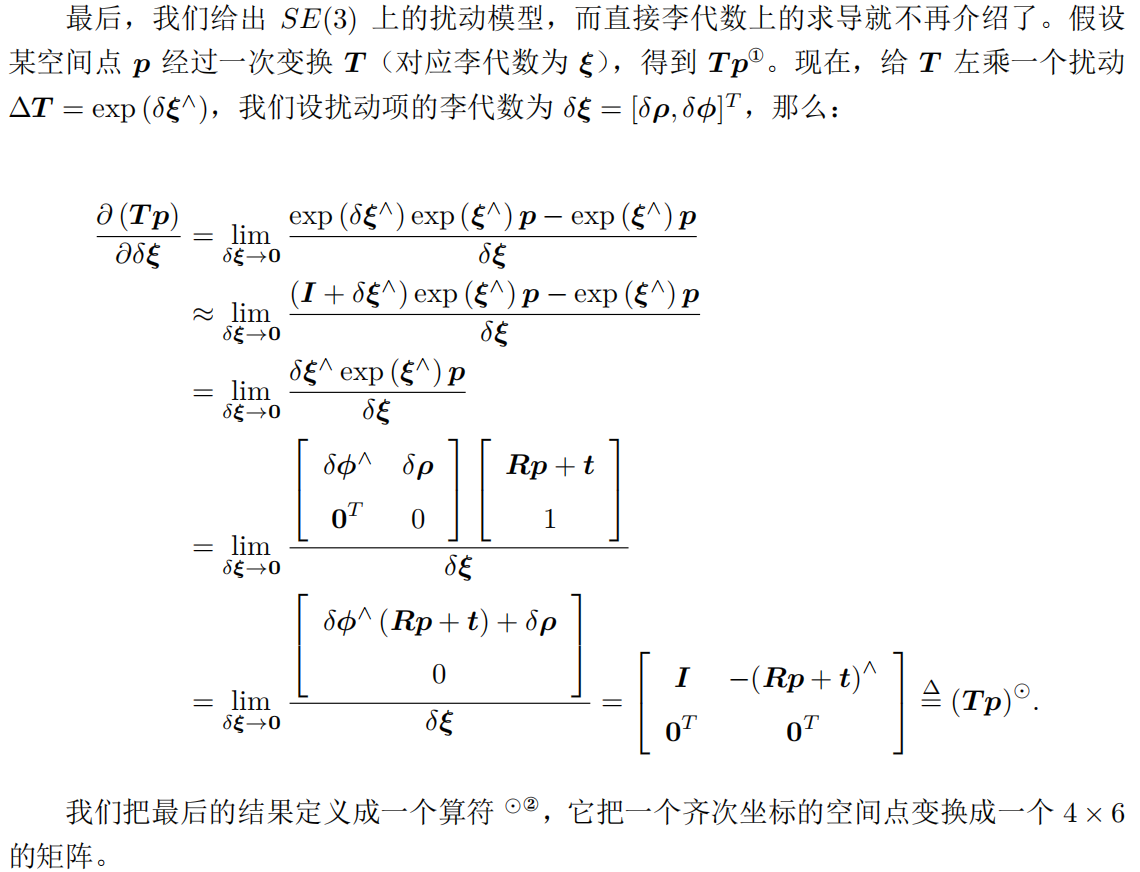
   第2、3行是因為用矩陣的等價無窮小替換；

四、評估軌跡的誤差

1. 向量的長度（或大小）

   1. 歐式距離

      在三維及三維以下的向量空間中，向量的長度的平方是坐標值的平方和。

   2. 歐式推廣

      在n維坐標系中，我們也可以用這一思想表示向量的長度（或者稱之為大小）。

      \[\overrightarrow{\alpha}=[\alpha_1，\alpha_2，\cdots，\alpha_n]^T，則||\overrightarrow{\alpha}||_2^2=\alpha_1^2+\alpha_2^2+\cdots+\alpha_n^2 \]

2. 矩陣的左右乘法區別

3. 每個位姿李代數誤差

   我們記第\(i\)時刻的真實軌跡為\(T_{(GT，i)}\)、觀測（估計）軌跡為\(T_{(Esti，i)}\)、絕對軌跡誤差\(T_{(ATE，i)}\)。

   由於誤差的作用使得真實軌跡變換到了估計軌跡，我們的關注點是坐標系的變換，所以有三者的轉換公式：\(T_{(Esti，i)}=T_{(GT，i)}\cdot{T_{(ATE，i)}}\)，即有\(T_{(ATE，i)}=T_{(GT，i)}^{-1}\cdot{T_{(Esti，i)}}\)。

   得到了每個位姿的誤差公式，那如何確定誤差的大小呢？我們知道李群是很難估計大小的，所以我們可以借助其對應的李代數來確定大小，這就需要用到對數映射公式：\(\xi=【\log(T)】^{\vee}\)。

   所以每個位姿的李代數上的誤差為：\(【\log(T_{(GT，i)}^{-1}\cdot{T_{(Esti，i)}})】^{\vee}\)，那么它的大小也就可以用二范數來計算。

   當然我們也可以計算第i時刻的鄰域\(\Delta{t}\)時間內，真實軌跡（的變化量）與估計軌跡（的變化量）的相對誤差：

   \[【\log（T_{(GT，i)}^{-1}\cdot{T_{(GT，i+\Delta{t})}}）^{-1}（T_{(Esti，i)}^{-1}\cdot{T_{(Esti，i+\Delta{t})}}）】^{\vee} \]