參數方程的幾何解釋
如果二維空間內有兩個點(2,1)和(0,2),那么經過這兩點的直線方程是什么?
初中的知識可以告訴我們,斜率是 \(k = \displaystyle\frac{y_2 - y_1}{x_2 - x_1}\) 。現在使用向量和參數方程來理解這個問題。假設在二維空間內有兩個向量 a<2,1> 和 b<0,2>,如下圖所示:
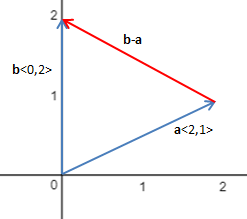
一個不太准確的說法是,將 b-a 的兩端延長,就是所求的直線,只要能夠恰當地表示這條直線就好了。由於向量表示的大小和方向的量,與位置無關,所以可以將 b-a 平移:

現在使用平移后的 b-a,它與 b 的線性組合就可以表示所求直線(向量終點站直線上):
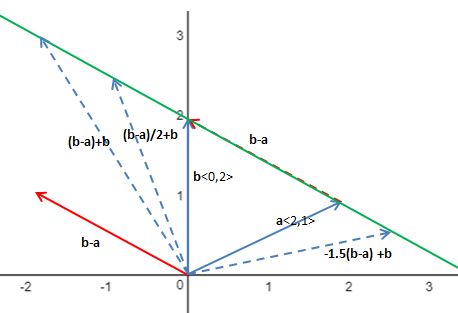
將 b-a 的倍數設為 t,那么直線可以表示為:

轉換成 x,y 的參數方程,x = -2t, y = 2 + t
