用python做時間序列預測七：時間序列復雜度量化

本文介紹一種方法,幫助我們了解一個時間序列是否可以預測，或者說了解可預測能力有多強。

Sample Entropy （樣本熵）

Sample Entropy是Approximate Entropy(近似熵)的改進，用於評價波形前后部分之間的混亂程度，
熵越大，亂七八糟的波動越多，越不適合預測；熵越小，亂七八糟的波動越小，預測能力越強。

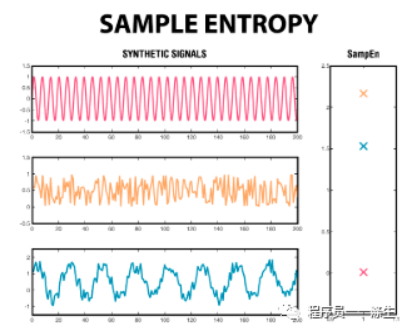
具體思想和實現如下：

• 思想
  Sample Entropy最終得到一個 -np.log(A/B) ，該值越小預測難度越小，所以A/B越大，預測難度越小。
  A：從0位置開始，取m+1個元素構成一個向量，然后移動一步，再取m+1個元素構成一個向量，如此繼續直到最后得到一個向量集合Xa,看有多少向量彼此的距離小於容忍度r(即有多少向量彼此相似，又稱自相似個數)。
  B：從0位置開始，取m個元素構成一個模板向量，然后移動一步，再取m個元素構成一個模板向量，如此繼續直到最后得到一個向量集合Xb，看有多少向量彼此的距離小於容忍度r(即有多少向量彼此相似，又稱自相似個數)。
  而實際上A總是小於等於B的，所以A/B越接近1，預測難度越小，直覺上理解，應該就是波形前后部分之間的變化不大，那么整個時間序列的波動相對來說會比較純(這也是熵的含義，熵越小，信息越純，熵越大，信息越混亂)，或者說會具有一定的規律，而如果A和B相差很大，則時間序列波動不純，或者說幾乎沒有規律可言。
  比如：U = [0.2, 0.6, 0.7, 1.2, 55, 66]，m=2,
  那么可以計算得到：
  Xa = [[0.2, 0.6, 0.7], [0.6, 0.7, 1.2], [0.7, 1.2, 55.0], [1.2, 55.0, 66.0]]
  Xb = [[0.2, 0.6], [0.6, 0.7], [0.7, 1.2], [1.2, 55.0], [55.0, 66.0]]
  假設Xa中相似向量的個數比Xb多，那么應該出現Xa滿足r，但是Xb不滿足r的情況，但是拿Xa和Xb的前兩個向量來分析，如果Xa滿足r，則0.2-0.6 ，0.6-0.7，0.7-1.2中的最大值應該<=r,也就是說0.2-0.6 ，0.6-0.7肯定<=r,如此推斷，Xb肯定也滿足r， 所以只有可能出現Xb滿足r，Xa不滿足r的情況。
• python實現

def SampEn(U, m, r):
    """
    用於量化時間序列的可預測性
    :param U: 時間序列
    :param m: 模板向量維數
    :param r: 距離容忍度，一般取0.1~0.25倍的時間序列標准差，也可以理解為相似度的度量閾值
    :return: 返回一個-np.log(A/B)，該值越小預測難度越小
    """
    def _maxdist(x_i, x_j):
        """
         Chebyshev distance
        :param x_i:
        :param x_j:
        :return:
        """
        return max([abs(ua - va) for ua, va in zip(x_i, x_j)])

    def _phi(m):
        x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)]
        C = [len([1 for j in range(len(x)) if i != j and _maxdist(x[i], x[j]) <= r]) for i in range(len(x))]
        return sum(C)

    N = len(U)
    return -np.log(_phi(m + 1) / _phi(m))
    
if __name__ == '__main__':
    _U = [0.2, 0.6, 0.7, 1.2, 55, 66]
    rand_small = np.random.randint(0, 100, size=120)
    rand_big = np.random.randint(0, 100, size=136)
    m = 2
    print(SampEn(_U, m, r=0.2 * np.std(_U)))
    print(SampEn(rand_small, m, r=0.2 * np.std(rand_small)))
    print(SampEn(rand_big, m, r=0.2 * np.std(rand_big)))    

ok,本篇就這么多內容啦~，感謝閱讀O(∩_∩)O。