title: 層次分析法
date: 2020-02-25 19:14:41
categories: 數學建模
tags: [MATLAB, 評價模型]
mathjax: true
定義
層次分析法（The Analytic Hierarchy Process即AHP)是由美國運籌學家、 匹茲堡大學教授T . L. Saaty於20世紀70年代創立的一種系統分析與決策的綜合 評價方法，是在充分研究了人類思維過程的基礎上提出來的，它較合理地解 決了定性問題定量化的處理過程。
AHP的主要特點是通過建立遞階層次結構，把人類的判斷轉化到若干因 素兩兩之間重要度的比較上，從而把難於量化的定性判斷轉化為可操作的重 要度的比較上面。在許多情況下，決策者可以直接使用AHP進行決策，極大 地提高了決策的有效性、可靠性和可行性，但其本質是一種思維方式，它把 復雜問題分解成多個組成因素，又將這些因素按支配關系分別形成遞階層次 結構，通過兩兩比較的方法確定決策方案相對重要度的總排序。整個過程體 現了人類決策思維的基本特征，即分解、判斷、綜合，克服了其他方法回避 決策者主觀判斷的缺點。
步驟
第一步遞階層次結構
分析系統中各因素之間的關系，建立系統的遞階層次結構。
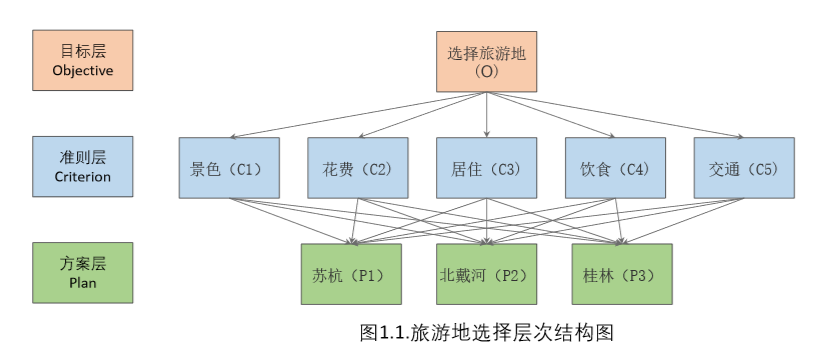
第二步構造判斷矩陣
{1，2，3，...，9}:代表重要程度，逐漸遞增
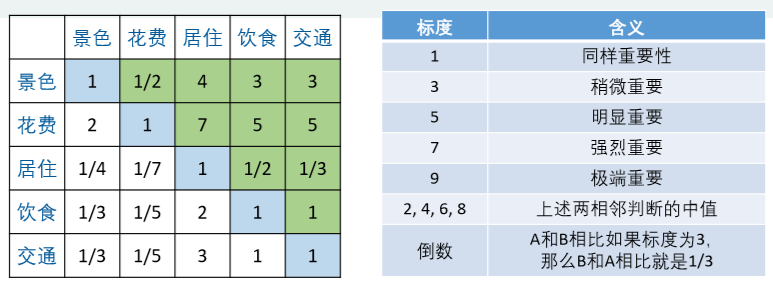
得到一個方陣，我們記為A，對應的元素為\(a_{ij}\).
（1）\(a_{ij}\)表示的意義是，與指標j相比，i的重要程度。
（2）當i=j時，兩個指標相同，因此同等重要記為1，這就解釋了主對角線元素為1。
（3）\(a_{ij}\)>0且滿足\(a_{ij}*a_{ji}=1\)（我們稱滿足這一條件的矩陣為正互反矩陣）
第三步一致性檢驗
判斷矩陣各行（各列）之間成倍數關系
\(a_{ij}\)>0且滿足\(a_{ij}*a_{ji}=1\)（我們稱滿足這一條件的矩陣為正互反矩陣）
在層次分析法中，我們構造的判斷矩陣均是正互反矩陣
若正互反矩陣滿足\(a_{ij}*a_{jk}=a_{ik}\)，則我們稱其為一致矩陣
注意：在使用判斷矩陣求權重之前，必須對其進行一致性檢驗。
\[\left[\begin{array}{cccc}{a_{11}} & {a_{12}} & {\cdots} & {a_{1 n}} \\{a_{21}} & {a_{22}} & {\cdots} & {a_{2 n}} \\{\vdots} & {\vdots} & {\ddots} & {\vdots} \\{a_{n 1}} & {a_{n 2}} & {\cdots} & {a_{n n}}\end{array}\right]為一致矩陣的充要條件：\left\{\begin{array}{l}{a_{ij}>0} \\{a_{11}=a_{22}=\cdots=a_{n n}=1} \\{\left[a_{i 1}, a_{i 2}, \cdots, a_{i n}\right]=k_{i}\left[a_{11}, a_{12}, \cdots, a_{1 n}\right]}\end{array}\right. \]
\[<Empty \space Math \space Block> \]
一致性檢驗的步驟
第一步：計算一致性指標CI
\[CI=\frac{入_{max}-n}{n-1} \]
第二步：查找對應的平均隨機一致性指標RI
第三步：計算一致性比例CR
\[CR=\frac{CI}{RI} \]
如果CR < 0.1, 則可認為判斷矩陣的一致性可以接受；否則需要對 判斷矩陣進行修正。
第四步判斷矩陣計算權重
歸一化
權重一定要進行歸一化處理
eg：
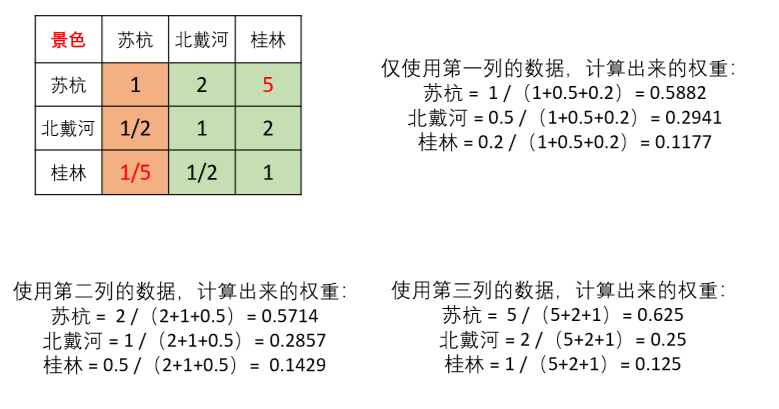
方法1：算術平均法求權重
-
第一步：將判斷矩陣按照列歸一化 （每一個元素除以其所在列的和）
-
第二步：將歸一化的各列相加(按行求和)
-
第三步：將相加后得到的向量中每個元素除以n即可得到權重向量
假設判斷矩陣為
\[A=\left[\begin{array}{cccc}{a_{11}} & {a_{12}} & {\cdots} & {a_{1 n}} \\{a_{21}} & {a_{22}} & {\cdots} & {a_{2 n}} \\{\vdots} & {\vdots} & {\ddots} & {\vdots} \\{a_{n 1}} & {a_{n 2}} & {\cdots} & {a_{n n}}\end{array}\right] \]
那么算術平均法求得的權重向量
\[\omega_{i}=\frac{1}{n} \sum_{j=1}^{n} \frac{a_{i j}}{\sum_{k=1}^{n} a_{k j}}（i=1，2，...n） \]
方法2：幾何平均法求權重
幾何平均法求權重也有三步：
-
第一步：將A的元素按照行相乘得到一個新的列向量
-
第二步：將新的向量的每個分量開n次方
-
第三步：對該列向量進行歸一化即可得到權重向量
-
假設判斷矩陣為
\[A=\left[\begin{array}{cccc}{a_{11}} & {a_{12}} & {\cdots} & {a_{1 n}} \\{a_{21}} & {a_{22}} & {\cdots} & {a_{2 n}} \\{\vdots} & {\vdots} & {\ddots} & {\vdots} \\{a_{n 1}} & {a_{n 2}} & {\cdots} & {a_{n n}}\end{array}\right] \]
那么幾何平均法求得的權重向量
\[\omega_{i}=\frac{\left(\prod_{j=1}^{n} a_{i j}\right)^{\frac{1}{n}}}{\sum_{k=1}^{n}\left(\prod_{j=1}^{n} a_{k j}\right)^{\frac{1}{n}}}, \quad(i=1,2, \cdots, n) \]
方法3：特征值法求權重
假如我們的判斷矩陣一致性可以接受，那么我們可以仿照一致矩陣權重的求法。
-
第一步：求出矩陣A的最大特征值以及其對應的特征向量
-
第二步：對求出的特征向量進行歸一化即可得到我們的權重
實際建模
以往的論文利用層次分析法解決實際問題時，都是采用其中某一種方法求權重，而不同的計算方法可能會導致結果有所偏差。為了保證結果的穩健性，本文采用了三種方法分別求出了權重，再根據得到的權重矩陣計算各方案的得分，並進行排序和綜合分析，這樣避免了采用單一方法所產生的偏差，得出的結論將更全面、更有效。
三種權值求平均權值
代碼
%% 注意：在論文寫作中，應該先對判斷矩陣進行一致性檢驗，然后再計算權重，因為只有判斷矩陣通過了一致性檢驗，其權重才是有意義的。
%% 在下面的代碼中，我們先計算了權重，然后再進行了一致性檢驗，這是為了順應計算過程，事實上在邏輯上是說不過去的。
%% 因此大家自己寫論文中如果用到了層次分析法，一定要先對判斷矩陣進行一致性檢驗。
%% 而且要說明的是，只有非一致矩陣的判斷矩陣才需要進行一致性檢驗。
%% 如果你的判斷矩陣本身就是一個一致矩陣，那么就沒有必要進行一致性檢驗。
% 在每一行的語句后面加上分號(一定要是英文的哦;中文的長這個樣子；)表示不顯示運行結果
% 多行注釋:選中要注釋的若干語句,快捷鍵Ctrl+R
% 取消注釋:選中要取消注釋的語句,快捷鍵Ctrl+T
disp('請輸入判斷矩陣A') %matlab中disp()就是屏幕輸出函數，類似於c語言中的printf（）函數
% 注意，disp函數比較特殊，這里可要分號，可不要分號哦
A=input('A=');
% 這里輸入的就是我們的判斷矩陣，其為n階方陣（行數和列數相同）
% [1 3 1/3 1/3 1 1/3;1/3 1 1/4 1/5 1 1/5;3 4 1 1 2 3;3 5 1 1 2 1;1 1 1/2 1/2 1 1;3 5 1/3 1 1 1]
% [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% 在開始下面正式的步驟之前，我們有必要檢驗下A是否因為粗心而輸入有誤
ERROR = 0; % 默認輸入是沒有錯誤的
%(1)檢查矩陣A的維數是否不大於1或不是方陣
[r,c]=size(A);
%size(A)函數是用來求矩陣的大小的,返回一個行向量，第一個元素是矩陣的行數，第二個元素是矩陣的列數
%[r,c]=size(A) %將矩陣A的行數返回到第一個輸出變量r，將矩陣的列數返回到第二個輸出變量c
if r ~= c || r <= 1
% 注意哦，不等號是 ~= (~是鍵盤Tab上面那個鍵，要和Shift鍵同時按才會出來)，別和C語言里面的!=搞混了
% ||表示邏輯運算符‘或’（在鍵盤Enter上面，也要和Shift鍵一起按） 邏輯運算符且是 && （&讀and，連接符號，是and的縮寫。 ）
ERROR = 1;
end
% Matlab的判斷語句，if所在的行不需要冒號，語句的最后一定要以end結尾 ；中間的語句要注意縮進。
%(2)檢驗是否為正互反矩陣 a_ij > 0 且 a_ij * a_ji = 1
if ERROR == 0
[n,n] = size(A);
% 因為我們的判斷矩陣A是一個非零方陣，所以這里的r和c相同，我們可以就用同一個字母n表示
% 判斷是否有元素小於0
% for i = 1:n
% for j = 1:n
% if A(i,j)<=0
% ERROR = 2;
% end
% end
% end
if sum(sum(A <= 0)) > 0
ERROR = 2;
end
end
%順便檢驗n是否超過了15，因為RI向量為15維
if ERROR == 0
if n > 15
ERROR = 3;
end
end
if ERROR == 0
% 判斷 a_ij * a_ji = 1 是否成立
if sum(sum(A' .* A ~= ones(n))) > 0
ERROR = 4;
end
% A' 表示求出 A 的轉置矩陣，即將a_ij和a_ji互換位置
% ones(n)函數生成一個n*n的全為1的方陣, zeros(n)函數生成一個n*n的全為0的方陣
% ones(m,n)函數生成一個m*n的全為1的矩陣
% MATLAB在矩陣的運算中，“/”號和“*”號代表矩陣之間的乘法與除法，對應元素之間的乘除法需要使用“./”和“.*”
% 如果a_ij * a_ji = 1 滿足， 那么A和A'對應元素相乘應該為1
end
if ERROR == 0
% % % % % % % % % % % % %方法1： 算術平均法求權重% % % % % % % % % % % % %
% 第一步：將判斷矩陣按照列歸一化（每一個元素除以其所在列的和）
% 第二步：將歸一化的各列相加
% 第三步：將相加后的向量除以n即可得到權重向量
Sum_A = sum(A);
% matlab中的sum函數的用法
% a=sum(x);%按列求和
% a=sum(x,2);%按行求和
% a=sum(x(:));%對整個矩陣求和
% % 基礎：matlab中如何提取矩陣中指定位置的元素？
% % （1）取指定行和列的一個元素（輸出的是一個值）
% % A(2,1) A(3,2)
% % （2）取指定的某一行的全部元素（輸出的是一個行向量）
% % A(2,:) A(5,:)
% % （3）取指定的某一列的全部元素（輸出的是一個列向量）
% % A(:,1) A(:,3)
% % （4）取指定的某些行的全部元素（輸出的是一個矩陣）
% % A([2,5],:) 只取第二行和第五行（一共2行）
% % A(2:5,:) 取第二行到第五行（一共4行）
% % （5）取全部元素(按列拼接的，最終輸出的是一個列向量)
% % A(:)
SUM_A = repmat(Sum_A,n,1);
% B = repmat(A,m,n):將矩陣A復制m×n塊，即把A作為B的元素，B由m×n個A平鋪而成。
% 另外一種替代的方法如下：
% SUM_A = [];
% for i = 1:n %循環哦，不需要加冒號，這里表示循環n次
% SUM_A = [SUM_A;Sum_A];
% end
Stand_A = A ./ SUM_A;
% MATLAB在矩陣的運算中，“*”號和“/”號代表矩陣之間的乘法與除法，對應元素之間的乘除法需要使用“./”和“.*”
% 這里我們直接將兩個矩陣對應的元素相除即可
disp('算術平均法求權重的結果為：');
disp(sum(Stand_A,2) / n)
% 首先對標准化后的矩陣按照行求和，得到一個列向量，然后再將這個列向量的每個元素同時除以n即可（注意這里也可以用./哦）
% % % % % % % % % % % % %方法2： 幾何平均法求權重% % % % % % % % % % % % %
% 第一步：將A的元素按照行相乘得到一個新的列向量
Prduct_A = prod(A,2);
% prod函數和sum函數類似，一個用於乘，一個用於加
% 第二步：將新的向量的每個分量開n次方
Prduct_n_A = Prduct_A .^ (1/n);
% 這里對元素操作，因此要加.號哦。 ^符號表示乘方哦 這里是開n次方，所以我們等價求1/n次方
% 第三步：對該列向量進行歸一化即可得到權重向量
% 將這個列向量中的每一個元素除以這一個向量的和即可
disp('幾何平均法求權重的結果為：');
disp(Prduct_n_A ./ sum(Prduct_n_A))
% % % % % % % % % % % % %方法3： 特征值法求權重% % % % % % % % % % % % %
% 計算矩陣A的特征值和特征向量的函數是eig(A),其中最常用的兩個用法：
% （1）E=eig(A)：求矩陣A的全部特征值，構成向量E。
% （2）[V,D]=eig(A)：求矩陣A的全部特征值，構成對角陣D，並求A的特征向量構成V的列向量。（V的每一列都是D中與之相同列的特征值的特征向量）
[V,D] = eig(A); %V是特征向量, D是由特征值構成的對角矩陣（除了對角線元素外，其余位置元素全為0）
Max_eig = max(max(D)); %也可以寫成max(D(:))哦~
% 那么怎么找到最大特征值所在的位置了？ 需要用到find函數，它可以用來返回向量或者矩陣中不為0的元素的位置索引。
% 下面例子來自博客：https://www.cnblogs.com/anzhiwu815/p/5907033.html
% 關於find函數的更加深入的用法可參考原文
% >> X = [1 0 4 -3 0 0 0 8 6];
% >> ind = find(X)
% ind =
% 1 3 4 8 9
% 其有多種用法，比如返回前2個不為0的元素的位置：
% >> ind = find(X,2)
% >> ind =
% 1 3
%若X是一個矩陣，索引該如何返回呢？
% >> X = [1 -3 0;0 0 8;4 0 6]
% X =
% 1 -3 0
% 0 0 8
% 4 0 6
% >> ind = find(X)
% ind =
% 1
% 3
% 4
% 8
% 9
% 這是因為在Matlab在存儲矩陣時，是一列一列存儲的，我們可以做一下驗證：
% >> X(4)
% ans =
% -3
% 假如你需要按照行列的信息輸出該怎么辦呢？
% [r,c] = find(X)
% r =
% 1
% 3
% 1
% 2
% 3
% c =
% 1
% 1
% 2
% 3
% 3
% [r,c] = find(X,1) %只找第一個非0元素
% r =
% 1
% c =
% 1
% 那么問題來了，我們要得到最大特征值的位置，就需要將包含所有特征值的這個對角矩陣D中，不等於最大特征值的位置全變為0
% 這時候可以用到矩陣與常數的大小判斷運算，共有三種運算符：大於> ;小於< ;等於 == （一個等號表示賦值；兩個等號表示判斷）
% 例如：A > 2 會生成一個和A相同大小的矩陣，矩陣元素要么為0，要么為1（A中每個元素和2比較，如果大於2則為1，否則為0）
[r,c]=find(D == Max_eig , 1);
% 找到D中第一個與最大特征值相等的元素的位置，記錄它的行和列。
disp('特征值法求權重的結果為：');
disp( V(:,c) ./ sum(V(:,c)) )
% 我們先根據上面找到的最大特征值的列數c找到對應的特征向量，然后再進行標准化。
% % % % % % % % % % % % %下面是計算一致性比例CR的環節% % % % % % % % % % % % %
% 當CR<0.10時，我們認為判斷矩陣的一致性可以接受；否則應對其進行修正。
CI = (Max_eig - n) / (n-1);
RI=[0 0.00001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %注意哦，這里的RI最多支持 n = 15
% 這里n=2時，一定是一致矩陣，所以CI = 0，我們為了避免分母為0，將這里的第二個元素改為了很接近0的正數
CR=CI/RI(n);
disp('一致性指標CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
disp('因為CR<0.10，所以該判斷矩陣A的一致性可以接受!');
else
disp('注意：CR >= 0.10，因此該判斷矩陣A需要進行修改!');
end
elseif ERROR == 1
disp('請檢查矩陣A的維數是否不大於1或不是方陣')
elseif ERROR == 2
disp('請檢查矩陣A中有元素小於等於0')
elseif ERROR == 3
disp('A的維數n超過了15，請減少准則層的數量')
elseif ERROR == 4
disp('請檢查矩陣A中存在i、j不滿足A_ij * A_ji = 1')
end
作業
評價下表中20條河流的水質情況。 注：含氧量越高越好；PH值越接近7越好；細菌總數越少越好；植物性營養物量介於10‐20之間最佳，超 過20或低於10均不好。
topsis作業，求出四個指標的權重。
代碼結果
請輸入判斷矩陣A
A=[1 2 1 4;1/2 1 1 5;1 1 1 3;1/4 1/5 1/3 1]
算術平均法求權重的結果為：
0.3619
0.2761
0.2831
0.0789
幾何平均法求權重的結果為：
0.3645
0.2725
0.2852
0.0779
特征值法求權重的結果為：
0.3670
0.2743
0.2813
0.0774
一致性指標CI=
0.0351
一致性比例CR=
0.0394
因為CR<0.10，所以該判斷矩陣A的一致性可以接受!