本文的閱讀等級:中級
一實(或復) 正交矩陣(orthogonal matrix) 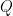 是一個實(或復) 方陣滿足
是一個實(或復) 方陣滿足
 ,
,
即  。 寫出
。 寫出 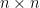 階實正交矩陣的行向量(column vector) 表達,
階實正交矩陣的行向量(column vector) 表達, 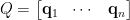 ,則
,則  ,矩陣乘積
,矩陣乘積  的
的 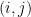 元等於
元等於 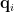 與
與  的內積。 因此,
的內積。 因此,  若
若  ,
,  若
若  。 換句話說,實正交矩陣
。 換句話說,實正交矩陣 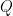 的行向量
的行向量  是向量空間
是向量空間 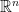 的一組單范正交基底(orthonormal basis),單范表示歸一,
的一組單范正交基底(orthonormal basis),單范表示歸一, 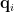 是單位向量,正交意味
是單位向量,正交意味 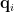 垂直
垂直  。 不過,復正交矩陣的行向量並非
。 不過,復正交矩陣的行向量並非  的一個單范正交集,因為兩個復向量
的一個單范正交集,因為兩個復向量 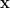 與
與  的內積定義為
的內積定義為  (見“ 內積的定義 ”)。 如欲將實正交矩陣推廣至復矩陣,將轉置改為共軛轉置。 一么正矩陣(酉矩陣,unitary matrix)
(見“ 內積的定義 ”)。 如欲將實正交矩陣推廣至復矩陣,將轉置改為共軛轉置。 一么正矩陣(酉矩陣,unitary matrix) 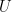 是一個復方陣滿足
是一個復方陣滿足
 ,
,
即  。 同樣地,設
。 同樣地,設  ,則
,則  。 么正矩陣的行向量
。 么正矩陣的行向量  是向量空間
是向量空間 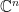 的一組單范正交基底。 例如,
的一組單范正交基底。 例如,
![U=\begin{bmatrix} \displaystyle\frac{1+i}{2}&\displaystyle\frac{1+i}{2}\\[0.8em] \displaystyle\frac{1-i}{2} &\displaystyle\frac{-1+i}{2} \end{bmatrix} U=\begin{bmatrix} \displaystyle\frac{1+i}{2}&\displaystyle\frac{1+i}{2}\\[0.8em] \displaystyle\frac{1-i}{2}&\displaystyle\frac{-1+i}{2} \end{bmatrix}](/image/aHR0cHM6Ly9zMC53cC5jb20vbGF0ZXgucGhwP2xhdGV4PVUlM0QlNUNiZWdpbiU3QmJtYXRyaXglN0QrKyU1Q2Rpc3BsYXlzdHlsZSU1Q2ZyYWMlN0IxJTJCaSU3RCU3QjIlN0QlMjYlNUNkaXNwbGF5c3R5bGUlNUNmcmFjJTdCMSUyQmklN0QlN0IyJTdEJTVDJTVDJTVCMC44ZW0lNUQrKysrJTVDZGlzcGxheXN0eWxlJTVDZnJhYyU3QjEtaSU3RCU3QjIlN0QlMjYlNUNkaXNwbGF5c3R5bGUlNUNmcmFjJTdCLTElMkJpJTdEJTdCMiU3RCsrKyslNUNlbmQlN0JibWF0cml4JTdEJmJnPWZmZmZmZiZmZz0wMDAwMDAmcz0w.png) ,
,
其中 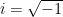 。 因為
。 因為  ,若
,若 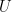 是一么正矩陣,則
是一么正矩陣,則  也是么正矩陣。 所以,么正矩陣
也是么正矩陣。 所以,么正矩陣 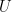 的共軛列向量(row vector) 構成
的共軛列向量(row vector) 構成 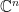 的一個單范正交集(事實上,
的一個單范正交集(事實上, 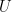 的列向量即構成單范正交集,因為
的列向量即構成單范正交集,因為  ,
,  也是么正矩陣)。 類似地,實正交矩陣
也是么正矩陣)。 類似地,實正交矩陣 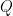 的列向量構成
的列向量構成 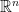 的一個單范正交集。 在一般情況下,么正矩陣與復正交矩陣是不同的,但實么正矩陣與實正交矩陣是相同的。 所以,么正矩陣的所有性質皆可套用於實正交矩陣。
的一個單范正交集。 在一般情況下,么正矩陣與復正交矩陣是不同的,但實么正矩陣與實正交矩陣是相同的。 所以,么正矩陣的所有性質皆可套用於實正交矩陣。
么正矩陣出現於許多矩陣分解式,舉兩個例子。 第一是矩陣三角化的Schur 定理:任一方陣 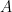 可分解為
可分解為  ,其中
,其中 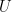 是一么正矩陣,
是一么正矩陣, 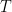 是上三角矩陣(見“ 矩陣三角化的Schur定理 ”)。 第二是正規矩陣(normal matrix) 的么正對角化(unitarily diagonalizable):若
是上三角矩陣(見“ 矩陣三角化的Schur定理 ”)。 第二是正規矩陣(normal matrix) 的么正對角化(unitarily diagonalizable):若 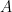 為一正規矩陣,
為一正規矩陣,  ,則存在一么正矩陣
,則存在一么正矩陣 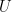 使得
使得  ,其中
,其中 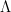 為一對角矩陣(見“ 特殊矩陣(2):正規矩陣 ”)。 事實上,可么正對角化是正規矩陣的一個充要條件。
為一對角矩陣(見“ 特殊矩陣(2):正規矩陣 ”)。 事實上,可么正對角化是正規矩陣的一個充要條件。
以下令 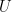 為一
為一 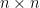 階么正矩陣,所有的性質都是由定義式得來。
階么正矩陣,所有的性質都是由定義式得來。
性質1 .向量的長度不因么正變換而改變,即每一  ,
,
 。
。
性質1說明么正變換是一個保長((length-preserving) 變換。使用定義式,
 。
。
反過來說,若所有向量  都滿足
都滿足  ,平方后整理可得
,平方后整理可得  ,可知
,可知  ,並推得
,並推得  。 所以,保長是么正矩陣的一個充要條件。
。 所以,保長是么正矩陣的一個充要條件。
性質2 .兩向量的內積不因么正變換而改變,即任何  ,
,
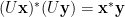 。
。
性質2說明么正變換具有內積不變性。 使用定義式,
 。
。
將上式的  替換為
替換為 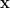 ,性質2可推得性質1。 所以,內積不變性是么正矩陣的另一個充要條件。
,性質2可推得性質1。 所以,內積不變性是么正矩陣的另一個充要條件。
性質3 .么正矩陣的特征值之絕對值為 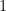 。
。
假設 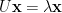 ,等號兩邊同時取向量長度。 利用性質1,等號左邊為
,等號兩邊同時取向量長度。 利用性質1,等號左邊為  ,但等號右邊為
,但等號右邊為  ,所以
,所以 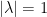 ,換句話說,么正矩陣的特征值可表示為
,換句話說,么正矩陣的特征值可表示為  。
。
性質4 .么正矩陣 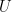 可么正對角化,
可么正對角化,  ,其中
,其中 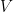 是一么正矩陣,
是一么正矩陣,  。
。
么正矩陣 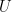 滿足
滿足  ,因此屬於正規矩陣家族,本身也可被么正對角化。 下面介紹
,因此屬於正規矩陣家族,本身也可被么正對角化。 下面介紹 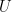 對應相異特征值的特征向量互為正交的一個證明。 假設非零向量
對應相異特征值的特征向量互為正交的一個證明。 假設非零向量 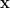 與
與  使得
使得  ,
,  ,且
,且  。 使用性質2,
。 使用性質2,
 。
。
比較等號兩邊,推得  或
或  。 使用性質三,令
。 使用性質三,令  ,則
,則  。 但已知
。 但已知 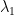 不等於
不等於  ,推論
,推論  ,證明
,證明 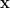 正交於
正交於  。
。
性質5 .么正矩陣 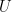 的行列式為
的行列式為  。
。
根據性質3, 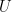 的特征值滿足
的特征值滿足  。 行列式等於特征值之積,故
。 行列式等於特征值之積,故  。 另一個作法計算
。 另一個作法計算
 ,
,
但  ,所以
,所以  。
。
對於一實正交矩陣 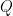 ,
,  為實數,由性質5可知
為實數,由性質5可知 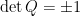 。 據此,實正交矩陣可以區分為兩類:若
。 據此,實正交矩陣可以區分為兩類:若  ,則
,則 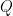 稱為適當的(proper) 的正交矩陣;若
稱為適當的(proper) 的正交矩陣;若  ,則
,則 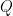 稱為不適當的正交矩陣。 令
稱為不適當的正交矩陣。 令  是平面上逆時針旋轉角為
是平面上逆時針旋轉角為  的旋轉矩陣,
的旋轉矩陣,  是平面上以
是平面上以  為鏡射軸指向的鏡射矩陣,公式如下(見“ 幾何變換矩陣的設計 ”):
為鏡射軸指向的鏡射矩陣,公式如下(見“ 幾何變換矩陣的設計 ”):
![R(\theta)=\left[\!\!\begin{array}{cr} \sin\theta&-\cos\theta\\ \cos\theta&\sin\theta \end{array}\!\!\ right],~~F(\phi)=\left[\!\!\begin{array}{cr} \cos 2\phi&\sin 2\phi\\ \sin 2\phi&-\cos 2\phi \ end{array}\!\!\right] R(\theta)=\left[\!\!\begin{array}{cr} \sin\theta&-\cos\theta\\ \cos\theta&\sin\theta \end{array}\!\!\right],~~F(\phi)=\left[\!\!\begin{array}{cr} \cos 2\phi&\sin 2\phi\\ \sin 2\phi&-\cos 2\phi \end{array}\!\!\right]](/image/aHR0cHM6Ly9zMC53cC5jb20vbGF0ZXgucGhwP2xhdGV4PVIlMjglNUN0aGV0YSUyOSUzRCU1Q2xlZnQlNUIlNUMlMjElNUMlMjElNUNiZWdpbiU3QmFycmF5JTdEJTdCY3IlN0QrKyU1Q3NpbiU1Q3RoZXRhJTI2LSU1Q2NvcyU1Q3RoZXRhJTVDJTVDKyslNUNjb3MlNUN0aGV0YSUyNiU1Q3NpbiU1Q3RoZXRhKyslNUNlbmQlN0JhcnJheSU3RCU1QyUyMSU1QyUyMSU1Q3JpZ2h0JTVEJTJDJTdFJTdFRiUyOCU1Q3BoaSUyOSUzRCU1Q2xlZnQlNUIlNUMlMjElNUMlMjElNUNiZWdpbiU3QmFycmF5JTdEJTdCY3IlN0QrKyU1Q2NvcysyJTVDcGhpJTI2JTVDc2luKzIlNUNwaGklNUMlNUMrKyU1Q3NpbisyJTVDcGhpJTI2LSU1Q2NvcysyJTVDcGhpKyslNUNlbmQlN0JhcnJheSU3RCU1QyUyMSU1QyUyMSU1Q3JpZ2h0JTVEJmJnPWZmZmZmZiZmZz0wMDAwMDAmcz0w.png) 。
。
因為  ,平面旋轉是適當的正交矩陣。 另一方面,
,平面旋轉是適當的正交矩陣。 另一方面,  ,平面鏡射是不適當的正交矩陣(見“ 旋轉與鏡射 ”)。 平面旋轉與鏡射是保長變換,提示我們這兩種矩陣是實正交矩陣。
,平面鏡射是不適當的正交矩陣(見“ 旋轉與鏡射 ”)。 平面旋轉與鏡射是保長變換,提示我們這兩種矩陣是實正交矩陣。
最后補充一個么正矩陣的充分條件:假設 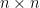 階矩陣
階矩陣 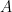 的特征值
的特征值 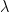 滿足
滿足 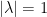 。 若每一
。 若每一  使得
使得  ,則
,則 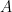 是一個么正矩陣(見“ 每周問題July 6, 2015 ”)。 注解提供兩個證明:第一個證明使用奇異值分解[1] ,第二個證明使用矩陣三角化的Schur定理[2] 。
是一個么正矩陣(見“ 每周問題July 6, 2015 ”)。 注解提供兩個證明:第一個證明使用奇異值分解[1] ,第二個證明使用矩陣三角化的Schur定理[2] 。
注解
[1] 令 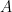 的特征值為
的特征值為  ,奇異值為
,奇異值為  。 給定的不等式等價於
。 給定的不等式等價於
 ,
,
其中  。 令
。 令 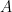 的奇異值分解為
的奇異值分解為  ,其中
,其中 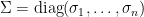 且
且  。 使用恆等式
。 使用恆等式  ,又
,又  且
且  ,推得
,推得  。 但
。 但  ,可知
,可知  。 因此,
。 因此,  ,即知
,即知  ,證明
,證明 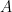 是一么正矩陣。
是一么正矩陣。
[2] 根據Schur 定理,寫出  ,其中
,其中 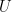 是么正矩陣,
是么正矩陣, ![T=[t_{ij}] T=[t_{ij}]](/image/aHR0cHM6Ly9zMC53cC5jb20vbGF0ZXgucGhwP2xhdGV4PVQlM0QlNUJ0XyU3QmlqJTdEJTVEJmJnPWZmZmZmZiZmZz0wMDAwMDAmcz0w.png) 是上三角矩陣,主對角元為
是上三角矩陣,主對角元為 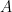 的特征值
的特征值  ,每一
,每一  。 考慮
。 考慮  ,其中
,其中  是第
是第 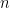 個標准單位向量,則
個標准單位向量,則  。 我們得到
。 我們得到
 。
。
對於單位向量 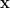 ,給定條件等價於
,給定條件等價於  ,再有
,再有  ,使得
,使得  ,
,  。 套用歸納法,重復上述步驟令
。 套用歸納法,重復上述步驟令  ,
,  ,可推論
,可推論 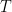 是一個對角矩陣滿足
是一個對角矩陣滿足  (因為
(因為  )。 所以,
)。 所以,
 。
。

