本文的阅读等级:中级
一实(或复) 正交矩阵(orthogonal matrix) 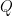 是一个实(或复) 方阵满足
是一个实(或复) 方阵满足
 ,
,
即  。 写出
。 写出 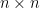 阶实正交矩阵的行向量(column vector) 表达,
阶实正交矩阵的行向量(column vector) 表达, 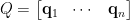 ,则
,则  ,矩阵乘积
,矩阵乘积  的
的 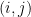 元等于
元等于 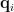 与
与  的内积。 因此,
的内积。 因此,  若
若  ,
,  若
若  。 换句话说,实正交矩阵
。 换句话说,实正交矩阵 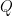 的行向量
的行向量  是向量空间
是向量空间 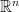 的一组单范正交基底(orthonormal basis),单范表示归一,
的一组单范正交基底(orthonormal basis),单范表示归一, 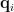 是单位向量,正交意味
是单位向量,正交意味 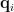 垂直
垂直  。 不过,复正交矩阵的行向量并非
。 不过,复正交矩阵的行向量并非  的一个单范正交集,因为两个复向量
的一个单范正交集,因为两个复向量 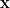 与
与  的内积定义为
的内积定义为  (见“ 内积的定义 ”)。 如欲将实正交矩阵推广至复矩阵,将转置改为共轭转置。 一么正矩阵(酉矩阵,unitary matrix)
(见“ 内积的定义 ”)。 如欲将实正交矩阵推广至复矩阵,将转置改为共轭转置。 一么正矩阵(酉矩阵,unitary matrix) 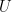 是一个复方阵满足
是一个复方阵满足
 ,
,
即  。 同样地,设
。 同样地,设  ,则
,则  。 么正矩阵的行向量
。 么正矩阵的行向量  是向量空间
是向量空间 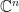 的一组单范正交基底。 例如,
的一组单范正交基底。 例如,
![U=\begin{bmatrix} \displaystyle\frac{1+i}{2}&\displaystyle\frac{1+i}{2}\\[0.8em] \displaystyle\frac{1-i}{2} &\displaystyle\frac{-1+i}{2} \end{bmatrix} U=\begin{bmatrix} \displaystyle\frac{1+i}{2}&\displaystyle\frac{1+i}{2}\\[0.8em] \displaystyle\frac{1-i}{2}&\displaystyle\frac{-1+i}{2} \end{bmatrix}](/image/aHR0cHM6Ly9zMC53cC5jb20vbGF0ZXgucGhwP2xhdGV4PVUlM0QlNUNiZWdpbiU3QmJtYXRyaXglN0QrKyU1Q2Rpc3BsYXlzdHlsZSU1Q2ZyYWMlN0IxJTJCaSU3RCU3QjIlN0QlMjYlNUNkaXNwbGF5c3R5bGUlNUNmcmFjJTdCMSUyQmklN0QlN0IyJTdEJTVDJTVDJTVCMC44ZW0lNUQrKysrJTVDZGlzcGxheXN0eWxlJTVDZnJhYyU3QjEtaSU3RCU3QjIlN0QlMjYlNUNkaXNwbGF5c3R5bGUlNUNmcmFjJTdCLTElMkJpJTdEJTdCMiU3RCsrKyslNUNlbmQlN0JibWF0cml4JTdEJmJnPWZmZmZmZiZmZz0wMDAwMDAmcz0w.png) ,
,
其中 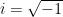 。 因为
。 因为  ,若
,若 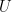 是一么正矩阵,则
是一么正矩阵,则  也是么正矩阵。 所以,么正矩阵
也是么正矩阵。 所以,么正矩阵 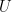 的共轭列向量(row vector) 构成
的共轭列向量(row vector) 构成 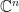 的一个单范正交集(事实上,
的一个单范正交集(事实上, 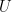 的列向量即构成单范正交集,因为
的列向量即构成单范正交集,因为  ,
,  也是么正矩阵)。 类似地,实正交矩阵
也是么正矩阵)。 类似地,实正交矩阵 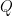 的列向量构成
的列向量构成 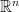 的一个单范正交集。 在一般情况下,么正矩阵与复正交矩阵是不同的,但实么正矩阵与实正交矩阵是相同的。 所以,么正矩阵的所有性质皆可套用于实正交矩阵。
的一个单范正交集。 在一般情况下,么正矩阵与复正交矩阵是不同的,但实么正矩阵与实正交矩阵是相同的。 所以,么正矩阵的所有性质皆可套用于实正交矩阵。
么正矩阵出现于许多矩阵分解式,举两个例子。 第一是矩阵三角化的Schur 定理:任一方阵 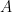 可分解为
可分解为  ,其中
,其中 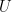 是一么正矩阵,
是一么正矩阵, 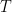 是上三角矩阵(见“ 矩阵三角化的Schur定理 ”)。 第二是正规矩阵(normal matrix) 的么正对角化(unitarily diagonalizable):若
是上三角矩阵(见“ 矩阵三角化的Schur定理 ”)。 第二是正规矩阵(normal matrix) 的么正对角化(unitarily diagonalizable):若 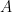 为一正规矩阵,
为一正规矩阵,  ,则存在一么正矩阵
,则存在一么正矩阵 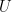 使得
使得  ,其中
,其中 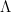 为一对角矩阵(见“ 特殊矩阵(2):正规矩阵 ”)。 事实上,可么正对角化是正规矩阵的一个充要条件。
为一对角矩阵(见“ 特殊矩阵(2):正规矩阵 ”)。 事实上,可么正对角化是正规矩阵的一个充要条件。
以下令 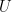 为一
为一 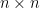 阶么正矩阵,所有的性质都是由定义式得来。
阶么正矩阵,所有的性质都是由定义式得来。
性质1 .向量的长度不因么正变换而改变,即每一  ,
,
 。
。
性质1说明么正变换是一个保长((length-preserving) 变换。使用定义式,
 。
。
反过来说,若所有向量  都满足
都满足  ,平方后整理可得
,平方后整理可得  ,可知
,可知  ,并推得
,并推得  。 所以,保长是么正矩阵的一个充要条件。
。 所以,保长是么正矩阵的一个充要条件。
性质2 .两向量的内积不因么正变换而改变,即任何  ,
,
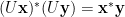 。
。
性质2说明么正变换具有内积不变性。 使用定义式,
 。
。
将上式的  替换为
替换为 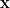 ,性质2可推得性质1。 所以,内积不变性是么正矩阵的另一个充要条件。
,性质2可推得性质1。 所以,内积不变性是么正矩阵的另一个充要条件。
性质3 .么正矩阵的特征值之绝对值为 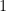 。
。
假设 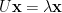 ,等号两边同时取向量长度。 利用性质1,等号左边为
,等号两边同时取向量长度。 利用性质1,等号左边为  ,但等号右边为
,但等号右边为  ,所以
,所以 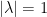 ,换句话说,么正矩阵的特征值可表示为
,换句话说,么正矩阵的特征值可表示为  。
。
性质4 .么正矩阵 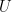 可么正对角化,
可么正对角化,  ,其中
,其中 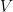 是一么正矩阵,
是一么正矩阵,  。
。
么正矩阵 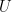 满足
满足  ,因此属于正规矩阵家族,本身也可被么正对角化。 下面介绍
,因此属于正规矩阵家族,本身也可被么正对角化。 下面介绍 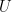 对应相异特征值的特征向量互为正交的一个证明。 假设非零向量
对应相异特征值的特征向量互为正交的一个证明。 假设非零向量 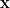 与
与  使得
使得  ,
,  ,且
,且  。 使用性质2,
。 使用性质2,
 。
。
比较等号两边,推得  或
或  。 使用性质三,令
。 使用性质三,令  ,则
,则  。 但已知
。 但已知 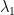 不等于
不等于  ,推论
,推论  ,证明
,证明 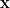 正交于
正交于  。
。
性质5 .么正矩阵 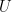 的行列式为
的行列式为  。
。
根据性质3, 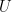 的特征值满足
的特征值满足  。 行列式等于特征值之积,故
。 行列式等于特征值之积,故  。 另一个作法计算
。 另一个作法计算
 ,
,
但  ,所以
,所以  。
。
对于一实正交矩阵 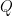 ,
,  为实数,由性质5可知
为实数,由性质5可知 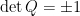 。 据此,实正交矩阵可以区分为两类:若
。 据此,实正交矩阵可以区分为两类:若  ,则
,则 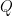 称为适当的(proper) 的正交矩阵;若
称为适当的(proper) 的正交矩阵;若  ,则
,则 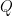 称为不适当的正交矩阵。 令
称为不适当的正交矩阵。 令  是平面上逆时针旋转角为
是平面上逆时针旋转角为  的旋转矩阵,
的旋转矩阵,  是平面上以
是平面上以  为镜射轴指向的镜射矩阵,公式如下(见“ 几何变换矩阵的设计 ”):
为镜射轴指向的镜射矩阵,公式如下(见“ 几何变换矩阵的设计 ”):
![R(\theta)=\left[\!\!\begin{array}{cr} \sin\theta&-\cos\theta\\ \cos\theta&\sin\theta \end{array}\!\!\ right],~~F(\phi)=\left[\!\!\begin{array}{cr} \cos 2\phi&\sin 2\phi\\ \sin 2\phi&-\cos 2\phi \ end{array}\!\!\right] R(\theta)=\left[\!\!\begin{array}{cr} \sin\theta&-\cos\theta\\ \cos\theta&\sin\theta \end{array}\!\!\right],~~F(\phi)=\left[\!\!\begin{array}{cr} \cos 2\phi&\sin 2\phi\\ \sin 2\phi&-\cos 2\phi \end{array}\!\!\right]](/image/aHR0cHM6Ly9zMC53cC5jb20vbGF0ZXgucGhwP2xhdGV4PVIlMjglNUN0aGV0YSUyOSUzRCU1Q2xlZnQlNUIlNUMlMjElNUMlMjElNUNiZWdpbiU3QmFycmF5JTdEJTdCY3IlN0QrKyU1Q3NpbiU1Q3RoZXRhJTI2LSU1Q2NvcyU1Q3RoZXRhJTVDJTVDKyslNUNjb3MlNUN0aGV0YSUyNiU1Q3NpbiU1Q3RoZXRhKyslNUNlbmQlN0JhcnJheSU3RCU1QyUyMSU1QyUyMSU1Q3JpZ2h0JTVEJTJDJTdFJTdFRiUyOCU1Q3BoaSUyOSUzRCU1Q2xlZnQlNUIlNUMlMjElNUMlMjElNUNiZWdpbiU3QmFycmF5JTdEJTdCY3IlN0QrKyU1Q2NvcysyJTVDcGhpJTI2JTVDc2luKzIlNUNwaGklNUMlNUMrKyU1Q3NpbisyJTVDcGhpJTI2LSU1Q2NvcysyJTVDcGhpKyslNUNlbmQlN0JhcnJheSU3RCU1QyUyMSU1QyUyMSU1Q3JpZ2h0JTVEJmJnPWZmZmZmZiZmZz0wMDAwMDAmcz0w.png) 。
。
因为  ,平面旋转是适当的正交矩阵。 另一方面,
,平面旋转是适当的正交矩阵。 另一方面,  ,平面镜射是不适当的正交矩阵(见“ 旋转与镜射 ”)。 平面旋转与镜射是保长变换,提示我们这两种矩阵是实正交矩阵。
,平面镜射是不适当的正交矩阵(见“ 旋转与镜射 ”)。 平面旋转与镜射是保长变换,提示我们这两种矩阵是实正交矩阵。
最后补充一个么正矩阵的充分条件:假设 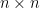 阶矩阵
阶矩阵 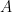 的特征值
的特征值 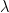 满足
满足 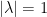 。 若每一
。 若每一  使得
使得  ,则
,则 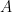 是一个么正矩阵(见“ 每周问题July 6, 2015 ”)。 注解提供两个证明:第一个证明使用奇异值分解[1] ,第二个证明使用矩阵三角化的Schur定理[2] 。
是一个么正矩阵(见“ 每周问题July 6, 2015 ”)。 注解提供两个证明:第一个证明使用奇异值分解[1] ,第二个证明使用矩阵三角化的Schur定理[2] 。
注解
[1] 令 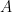 的特征值为
的特征值为  ,奇异值为
,奇异值为  。 给定的不等式等价于
。 给定的不等式等价于
 ,
,
其中  。 令
。 令 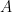 的奇异值分解为
的奇异值分解为  ,其中
,其中 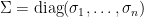 且
且  。 使用恒等式
。 使用恒等式  ,又
,又  且
且  ,推得
,推得  。 但
。 但  ,可知
,可知  。 因此,
。 因此,  ,即知
,即知  ,证明
,证明 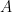 是一么正矩阵。
是一么正矩阵。
[2] 根据Schur 定理,写出  ,其中
,其中 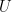 是么正矩阵,
是么正矩阵, ![T=[t_{ij}] T=[t_{ij}]](/image/aHR0cHM6Ly9zMC53cC5jb20vbGF0ZXgucGhwP2xhdGV4PVQlM0QlNUJ0XyU3QmlqJTdEJTVEJmJnPWZmZmZmZiZmZz0wMDAwMDAmcz0w.png) 是上三角矩阵,主对角元为
是上三角矩阵,主对角元为 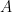 的特征值
的特征值  ,每一
,每一  。 考虑
。 考虑  ,其中
,其中  是第
是第 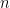 个标准单位向量,则
个标准单位向量,则  。 我们得到
。 我们得到
 。
。
对于单位向量 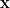 ,给定条件等价于
,给定条件等价于  ,再有
,再有  ,使得
,使得  ,
,  。 套用归纳法,重复上述步骤令
。 套用归纳法,重复上述步骤令  ,
,  ,可推论
,可推论 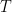 是一个对角矩阵满足
是一个对角矩阵满足  (因为
(因为  )。 所以,
)。 所以,
 。
。

