今天要給大家分享的統計方法是馬爾可夫多態模型,思路來源是下面這篇文章:
Ward DD, Wallace LMK, Rockwood K
Cumulative health deficits, APOE genotype, and risk for later-life mild cognitive impairment and dementia
Journal of Neurology, Neurosurgery & Psychiatry 2021;92:136-142.
我們知道輕度認知損害隨着時間的發展有可能會發展成痴呆,也可能會恢復,有可能不變,那這篇文章要解決的問題就是找到引起人群不同認知狀態變化的風險因子,因子其實有很多啦,作者本文只關注一個,叫做年齡相關的健康赤字(age-related health deficits)。作者想探討年齡相關的健康赤字是如何對認知狀態的轉換起作用的。
作者用了馬爾可夫多態模型Markov multi-state models回答了自己的研究問題,相應地,如果你的感興趣的結局變量是分類變量,比如狀態,並且各種狀態之間可以相互轉換,你想看看到底哪些因素影響了某種轉化的風險,那么今天介紹的馬爾可夫多態模型就值得你好好研究下了。
多態馬爾可夫模型
要理解多態馬爾可夫模型multistate Markov models,首先要知道馬爾可夫過程(Markov process)
馬爾可夫過程(Markov process)是一類隨機過程,因為是俄國數學家A.A.馬爾可夫於1907年提出來的,所以有了這么個名字。該過程就是說:在已知目前狀態(現在)的條件下,它未來的演變(將來)不依賴於它以往的演變 (過去 )。這種已知“現在”的條件下,“將來”與“過去”獨立的特性稱為馬爾可夫性質,具有這種性質的隨機過程叫做馬爾可夫過程,最簡單的馬爾可夫過程就是一階過程,每一個狀態的轉移只依賴於其之前的那一個狀態。
假設這個模型的每個狀態都只依賴於之前的狀態,這個假設被稱為馬爾科夫假設,這個假設可以大大地簡化具有馬爾可夫過程的隨機性問題。
現在給出馬爾可夫模型的說明
The Markov models stand out as much simpler than other models from a probability point of view, and this simplifies the likelihood evaluation
可以理解為馬爾可夫模型是對狀態改變情況的合理的簡化假設。那么我們接着看多態模型:
多態模型的基本說明如下圖:

就是說多態模型是來探討轉換狀態的,一個個體在觀測的特定時期一定是處於確定數量狀態中的一種,對於這類情況我們就可以用多態模型來研究。如果這些狀態的轉換如果滿足馬爾可夫性質,此時就叫做馬爾可夫多態模型。
就是你手上恰好有縱向隨訪數據,結局變量是分類變量(連續變量也可以轉化成有臨床意義的分類變量),你好奇隨着時間的變化,個體的在各個類別的轉化情況是怎么樣的,以及影響轉化概率的因素有哪些,那么就可以考慮使用多態模型。
A multi-state model describes how an individual moves between a series of states in continuous time
經典的多態模型就是研究疾病狀態轉換時使用的多態馬爾可夫多態模型,模型圖示如下:就是一個病人疾病可以加深可以恢復,並且隨時都可能死亡的多態模型,在這種模型中,下次狀態的改變只和當前狀態有關
in which individuals can advance or recover between adjacent disease states, or die from any state.:
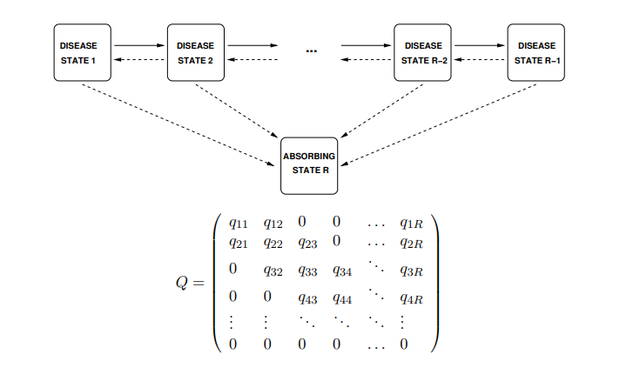
Fitting multi-state models to panel data generally relies on the Markov assumption, that future evolution only depends on the current state.
常見的操作就是使用多態Markov模型(Multi-states Markov model,MSM)利用縱向數據估計特定人群在不同時間內健康狀態的轉換概率,並對其健康狀態的轉換風險進行多因素探討,這兒也給大家貼兩篇多態馬爾可夫模型的中文文獻,感興趣的同學可以自行去下載查看:
展元元, 韓耀風, 方亞. 基於多狀態Markov模型的我國老年人無失能期望壽命及其影響因素. 中華流行病學雜志, 2021, 42(6): 1024-1029
石舒原, 趙厚宇, 劉志科, 楊晴晴, 沈鵬, 詹思延, 林鴻波, 孫鳳. 多狀態馬爾科夫模型估計2型糖尿病患者慢性並發症累積數量的轉移概率及影響因素研究. 中華流行病學雜志, 2021, 42(7): 1274-1279
反正我覺得這個模型對做科研的臨床醫生應該挺有用的吧,值得去學習的。
論文報告方法
依然是回到我們文章開頭提到的文章中,文章中是有畫一個狀態轉化的示意圖的,如下:
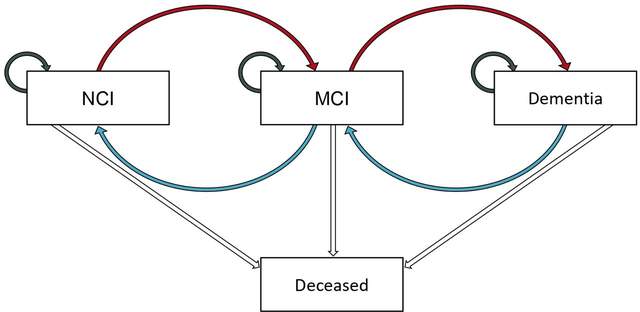
在文章中作者定義了3種狀態NCI, MCI and dementia,並且認為轉換過程可以向前也可以向后,並且隨時可以死亡,但是轉換只能在相鄰兩種狀態之間轉換而不能跳躍(當然做統計的時候這些條件都是可以自己根據客觀情況設定的)。論文報告了各個狀態的轉換次數和相應轉換方式的轉換概率,如圖:

就是所作者報告了各個狀態轉換的次數和轉換概率,這個很好理解。
結合研究問題,文章最重要的結果信息就是年齡相關的健康赤字frailty index score對狀態轉換的影響究竟如何,作者給出了不同亞組健康赤字對不同轉換的HR的森林圖:
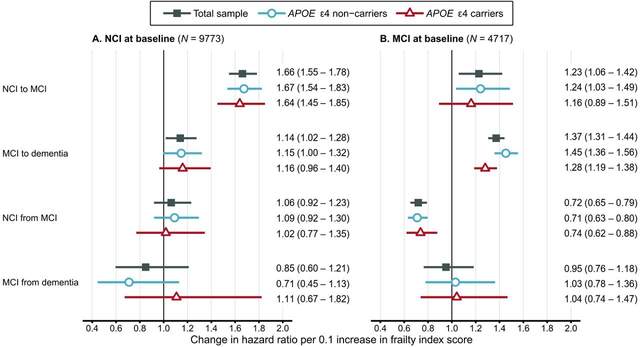
可以看到,frailty index score對每條作者關心的轉換方式的HR都是有展示的,並且好多亞組的結果都呈現在了上圖中,比如通過上圖我們就可以知道,無論是否攜帶APOE,frailty index score的增長總是會使得從NCI轉換成MCI,和MCI轉換成痴呆的風險變高。
根據上面的結果作者就明白了年齡相關的健康赤字究竟是如何影響痴呆狀態發生發展的。
上面基本上就是論文的主要分析,細枝末節大家自己去看原文哈,我們接着看操作。
實例操練
我現在手上有如下數據集:
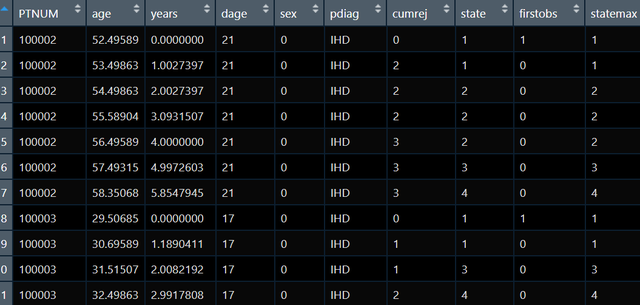
其中PTNUM是病人編號,age是每次隨訪的年齡,year是隨訪時時間,state是隨訪時的狀態總共有4種,我現在想做馬爾可夫多態模型看一下究竟是哪些因素影響了各個狀態轉換,在做多態模型的時候需要將同一個病人的數據放一起,並且個體內隨訪時間應該升序排列(就像上圖一樣的):
observations from the same subject must be adjacent in the dataset, and observations must be ordered by time within subjects.
數據這么處理后我們就可以很方便地統計出狀態轉化次數矩陣,代碼如下:
statetable.msm(state, PTNUM, data=cav)轉換次數輸出結果如下:
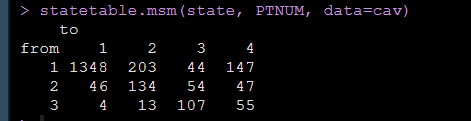
上面的結果就顯示了隨着隨訪的進行,有多少人從一個狀態轉化到了另外一個狀態,就是論文中報告的每個轉化的轉化次數,我們還可以使用pmatrix.msm函數得到轉化概率矩陣,如下圖:
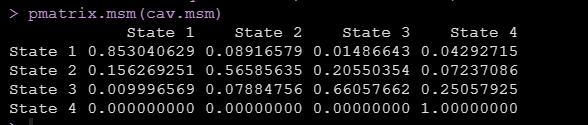
有了狀態轉換次數和狀態轉換概率,論文中的table2就出來了。
再繼續探討狀態轉換的影響因素,在探究狀態轉化影響因素之前,我們需要設定一個轉化的限制矩陣,比如論文中的狀態轉化情況就可以用如下矩陣表示:
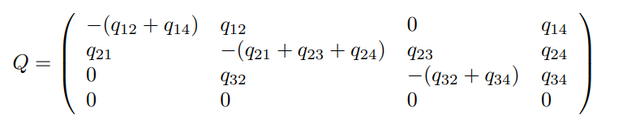
就是說我可以從狀態1NCI轉換到狀態2MCI,也可以從MCI轉回NCI,每一種狀態也都可以轉成狀態4死亡,但是也不能跨狀態轉換,而且死亡之后也不可能轉換成狀態1,2,3。那么相應的不可轉換的情況在矩陣中都要固定為0。
狀態轉換的情況我們根據實際設定好之后我們就可以運行多態模型了,代碼如下:
msm_model <- msm(state ~ years, subject = PTNUM, data = mydata, covariates = ~ dage + ihd, qmatrix = twoway4.q, death = 4, method = "BFGS", control = list(fnscale = 4000, maxit = 10000))代碼運行的過程就是就是去尋找最符合我們數據maximise the likelihood的同時又滿足我們設定的轉換參數的過程。
運行上面的代碼即可得到相應影響因素的HR和置信區間,比如兩個協變量dage和ihd對各個狀態轉化情況的HR如下:
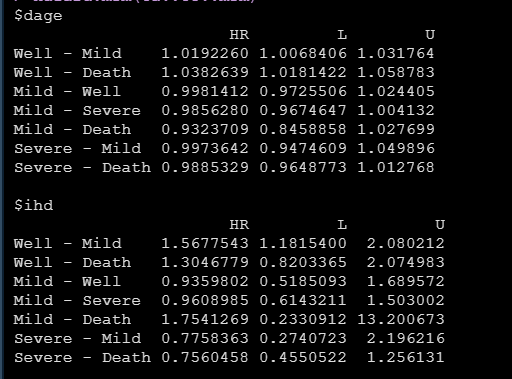
后面的工作就是根據各個亞組的HR和置信區間將森林圖做出來,然后對標論文就算完成啦。今天的分享就到這兒。
小結
今天給大家寫了馬爾可夫多態模型的原理的做法,希望能給到大家一些思路上的啟發,感謝大家耐心看完,自己的文章都寫的很細,重要代碼都在原文中,希望大家都可以自己做一做,請轉發本文到朋友圈后私信回復“數據鏈接”獲取所有數據和本人收集的學習資料。如果對您有用請先記得收藏,再點贊分享。
也歡迎大家的意見和建議,大家想了解什么統計方法都可以在文章下留言,說不定我看見了就會給你寫教程哦,有疑問歡迎私信,有合作意向請直接滴滴我。
