最小生成樹
Prim算法
算法思想:從圖中任意取出一個頂點,把它當成一顆樹,然后從與這棵樹相連接的邊中選取一條最短的(權值最小)的邊,並將這條邊及其所連接的頂點並入到當前樹中。
生成樹生成過程
候選邊長的算法:此時樹中只有0這個頂點,與0相連接的頂點分別為1、2、3長度分別為5、1、2這個長度就是候選邊的邊長,如果后續有其他頂點加入到生成樹中,也需要把新加入的頂點可能到達的邊加入到候選邊長中。
一、如圖a所示,先選取點0,然后選取候選邊的邊長分別為5、1和2,最小邊長為1;
二、如圖b所示,選取邊長為1的邊,此時候選邊長分別為5、3、2、6和2,最小邊長為2;

三、如圖c所示,選取邊長為2的邊,此時候選邊的邊長分別為5、3、2和3,其中最小邊長為2;
四、選取邊長為2的邊,此時候選邊長分別為3、4、5、,其中最小邊長為3

五、選取邊長為3的邊,此時所有頂點都已並入樹中,生成樹求解完畢

Prime算法執行過程
從樹中某一個頂點v0開始,構造生成樹的算法執行過程如下:
1)將v0到其他頂點的所有邊當作候選邊;
2)重復以下步驟n-1次,使得其他n-1個頂點被並入到生成樹中。
- 從候選邊中挑選出權值最小的邊輸出,並將與該邊另一端相接的頂點v並入到生成樹中;
- 考察所有剩余頂點vi,如果(v,vi)的權值比lowcost[vi],則用(v,vi)的權值更新lowcost[vi]
Prime算法代碼
void Prim(MGraph g, int v0, int &sum) {
int lowcost[maxSize], vset[maxSize], v;
int i, j, k, min;
v = v0;
for (i = 0; i < g.n; ++i) {
lowcost[i] = g.edges[v0][i];
vset[i] = 0;
}
vset[v0] = 1; // 將v0並入樹中
sum = 0; // sum清零用來累計樹的權值
for (i = 0; i < g.n-1; ++i) {
min = INF; // INF是一個已經定義的比圖中所有邊權值都大的常量
// 下面這個循環用於選出候選邊中的最小者
for (j = 0; j < g.n; ++j) {
if (vset[j] == 0 && lowcost[j] < min) { // 選出當前生成樹其他頂點到最短邊中最短的一條
min = lowcost[j];
k = j;
}
vset[k] = 1;
v = k;
sum += min; // 這里用sum記錄了最小生成樹的權值
// 下面這個循環以剛進入的頂點v為媒介更新候選邊
for (j = 0; j < g.n; ++j) {
if (vset[j] == 0 && g.edges[v][j] < lowcost[j]) {
lowcost[j] = g.edges[v][j];
}
}
}
}
}
Kruskal算法
每次找出候選邊中權值最小的邊,就將改變並入生成樹中。重復直至所有邊都被檢測完
Kruskal算法執行過程
總思想:每次找到候選邊中權值最小的邊,將該邊並入到生成樹中。- 先找到圖a中權值最小的邊為1
- 將權值為1的邊兩端連接並入到生成樹中,查找到下一個最小的權值為2

- 此時有兩個權值為2的邊,將其中一個與生成樹進行連接,我選擇的是2-4這條邊,0-3這條邊也可以。再次查找到最小的權值為2
- 將權值為2的邊與生成樹進行連接,此時還剩下點1,點1能連接到生成樹中的最小邊長為3

- 將點1與生成樹進行連接,最后所有的點都並入到生成樹中,算法結束。

相關存儲結構
| 數組下標 | 邊的信息 | 邊的權值 |
|---|---|---|
| 0 | (0,1) | 5 |
| 1 | (0,2) | 1 |
| 2 | (0,3) | 2 |
| 3 | (1,2) | 3 |
| 4 | (2,3) | 6 |
| 5 | (1,4) | 4 |
| 6 | (2,4) | 2 |
| 7 | (3,4) | 3 |
Kruskal算法代碼
typedef struct {
int a, b; // a和b為一條邊所連的兩個頂點
int w; // 邊的權值
}Road;
Road road[maxSize];
int v[maxSize]; // 定義並查集數組
int getRoot(int a) { //取根節點
while (a != v[a]) // 在並查集中查找根結點的函數
a = v[a]; //當a等於v[a]時找到根節點
return a;
}
根據下圖所示,只有根節點結點與上一個結點相同,即0為根節點
| 結點 | 上一個節點 |
|---|---|
| 0 | 0 |
| 1 | 2 |
| 2 | 0 |
| 3 | 0 |
| 4 | 2 |
 |
void Kruskal(MGraph g, int &sum, Road road[]) {
int i, N, E, a, b;
N = g.n;
E = g.e;
sum = 0;
for (i = 0; i < N; ++i) v[i] = i;
sort(road, E); // 對road數組中的E條邊按其權值從小到大排序, 假設該函數已定義好
for (i = 0; i < E; ++i) {
a = getRoot(road[i].a);
b = getRoot(road[i].b);
if (a != b) {
v[a] = b;
sum += road[i].w;
}
}
}
最短路徑
Dijkstra算法
不適合用於有負權值的帶權圖
Dijkstra算法代碼
void Dijkstra(MGraph g, int v, int dist[], int path[]) {
int set[maxSize];
int min, i, j, u;
// 從這句開始對各數組進行初始化
for (i = 0; i < g.n; ++i) {
dist[i] = g.edges[v][i];
set[i] = 0;
if (g.edges[v][i] < INF)
path[i] = v;
else {
path[i] = -1;
}
}
set[v] = 1; path[v] = -1;
// 初始化結束
// 關鍵操作開始
for (i = 0; i < g.n-1; ++i) {
min = INF;
// 這個循環每次從剩余頂點中選出一個頂點,通往這個頂點的路徑在通往所有剩余頂點的路徑中是長度最短的
for (j = 0; j < g.n; ++j) {
if (set[j] == 0 && dist[j] < min) {
u = j;
min = dist[j];
}
}
set[u] = 1; // 將選出的頂點並入最短路徑中
// 這個循環以剛並入的頂點作為中間點,對所有通往剩余頂點的路徑進行檢測
for (j = 0; j < g.n; ++j) {
// 這個if語句判斷頂點u的加入是否為出現通往頂點j的更短的路徑
if (set[j] == 0 && dist[u]+g.edges[u][j] < dist[j]) {
dist[j] = dist[u] + g.edges[u][j];
path[j] = u;
}
}
}
}
Floyd算法
不能解決帶有負權回路圖,可解決負權值圖
Floyd算法代碼
void Floyd(MGraph g, int Path[][maxSize]) {
int i, j, k;
int A[maxSize][maxSize];
// 這個雙循環對數組A[][]和Path[][]進行了初始化
for (i = 0; i < g.n; ++i) {
for (j = 0; j < g.n; ++j) {
A[i][j] = g.edges[i][j];
Path[i][j] = -1;
}
}
// 下面三層循環是主要操作,完成了以k為中間點對所有的頂點對{i, }進行檢測和修改
for (k = 0; k < g.n; ++k) {
for (i = 0; i < g.n; ++i) {
for (j = 0; j < g.n; ++j) {
if (A[i][j] > A[i][k] + A[k][j]) {
A[i][j] = A[i][k] + A[k][j];
Path[i][j] = k;
}
}
}
}
}
拓撲排序
AOV網
Aov網是一種以頂點表示活動、以邊表示活動先后次序且沒有回路的有向圖
在一個有向圖中找到拓撲排序的過程如下:
① 從有向圖中選擇一個沒有前驅(入度為零)的頂點輸出;
② 刪除①中的頂點,並刪除剩余圖中從該頂點發出的全部邊;
③重復上述兩步,直到剩余的圖中不存在沒有前驅的頂點為止。
下面來舉個例子:
某產品生產過程如圖所示: 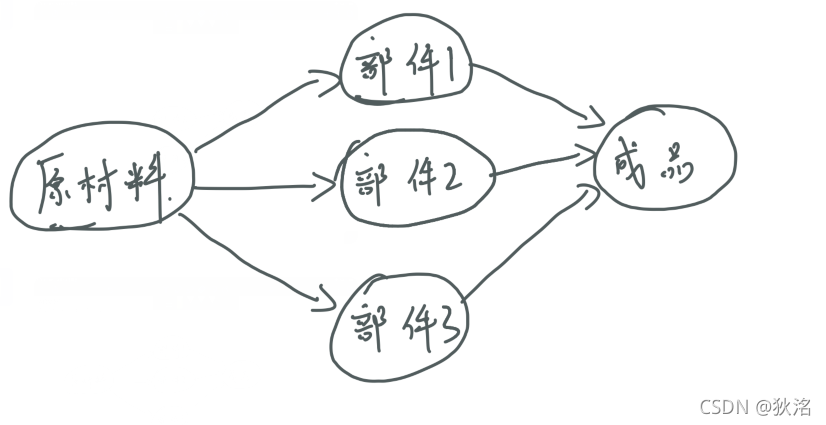-
先找到入度為零的頂點,即為原材料頂點,刪除該頂點,並刪除該頂點出發的所有邊

-
這時會發現部件1、部件2、部件3入度都為0,這時可以選擇這三個中的任意一個,我選擇的部件1

按照上邊1、2兩步刪除部件2,部件3

拓撲排序中對鄰接表表頭結構的修改
typedef struct {
char data;
int count; // 此處為新增代碼,count用來統計頂點當前的入度
ArcNode *firstarc;
}VNode;
拓撲排序算法代碼
【分析】:先找到所有入度為0的頂點,將它們壓入入stack[ ]棧中,然后出棧,出棧時將以此次出棧點為firstarc的頂點的入度全部減1,再次進行遍歷,查看是否有新的入度為0的頂點,如果有就將它入棧
int TopSort(AGraph *G) { //使用指針是為了避免整個圖的復制
int i, j, n = 0; //n 是用於統計輸出頂點的個數
int stack[maxSize], top = -1; // 定義並初始化棧、棧中保存所有入度為0的頂點
ArcNode *p;
// 這個循環將圖中入度為0的頂點入棧
for (i = 0; i < G->n; ++i) { // 圖中的頂點從0開始編號
if (G->adjlist[i].count == 0) {
stack[++top] = i;
}
}
// 關鍵操作開始
while (top != -1) {
i = stack[top--]; // 頂點出棧
++n; // 計數器加1,統計當前頂點
cout << i << " "; // 輸出當前頂點
p = G->adjlist[i].firstarc;
// 這個循環實現了將所有由此頂點引出的邊所指向的頂點的入度都減少1
// 並將這個過程中入度變為0的頂點入棧
while (nullptr != p) {
j = p->adjvex;
--(G->adjlist[j].count);
if (G->adjlist[j].count == 0)
stack[++top] = j;
p = p->nextarc;
}
}
// 關鍵操作結束
return n == G->n;
}
算法的對比
| BFS | DFS | Prime | Kruskal | Dijkstra | Floyd | |
|---|---|---|---|---|---|---|
| 無權圖 | √ | √ | √ | |||
| 帶權圖 | × | √ | √ | |||
| 帶負值的圖 | × | × | √ | |||
| 帶負值的網絡圖 | × | × | × | |||
| 時間復雜度 | ||||||
| 通常用於 |
表的對比
| 鄰接矩陣 | 鄰接表 | 十字鏈表 | 鄰接多重表 | |
|---|---|---|---|---|
| 空間復雜度 | O(| \(v^{2}\) |) | 無向圖O(| v | + 2| E |) 有向圖O(| v | + | E |) |
O(| v | + | E |) | O(| v | + | E |) |
| 找相鄰邊 | 遍歷對應行或列 時間復雜度為O(| v |) |
找有向圖的入邊必須遍歷 整個鄰接表 |
很方便 | 很方便 |
| 刪除邊或頂點 | 刪除邊很方便 刪除頂點需要大量移動數據 |
無向圖中刪除邊或頂點 都不方便 |
很方便 | 很方便 |
| 適用於 | 稠密圖 | 稀疏圖和其他 | 只能存有向圖 | 只能存無向圖 |
| 表示方式 | 唯一 | 不唯一 | 不唯一 | 不唯一 |
| Adjacent(G,x,y) | O(| 1 |) | O(| 1 |) ~ O(| v |) | ||
| Neighbors(G,x) | 無向圖:O(| v |) 有向圖:O(| v |) |
無向圖:O(| 1 |) ~ O(| v |) 有:出邊O(| 1 |) ~ O(| v |) 入邊:O(| E |) |
||
| InsertVertex(G,x) | O(| 1 |) | O(| 1 |) | ||
| DeleteVertex(G,x) | O(| v |) | O(| 1 |) ~ O(| E |) 有:刪出邊O(| 1 |) ~ O(| v |) 刪入邊O(| E |) |
||
| AddEdge(G,x,y) | O(| 1 |) | O(| 1 |) | ||
| FirstNeighbor(G,x) | 無:O(| 1 |) ~ O(| v |) 有:O(| 1 |) ~ O(| v |) |
無: O(| 1 |) 有:找出邊 O(| 1 |) 找入邊O(| 1 |) ~ O(| E |) |
||
| NextNeighbor(G,x,y) | O(| 1 |) ~ O(| V |) | O(| 1 |) | ||
| Get_edg_value(G,x,y) | O(| 1 |) | O(| 1 |) ~ O(| V |) | ||
| Set_edge_value(G,x,y,v) | O(| 1 |) | O(| 1 |) ~ O(| V |) |
錯題
- 鄰接矩陣適用於有向圖和無向圖的存儲,但不能存儲帶權的有向圖和無向圖,而只能使用鄰接表存儲形式來存儲它。(×)
【解析】 鄰接矩陣存儲帶權圖時,若Vi-Vj存在路徑,則在矩陣中的(i,j)位置寫入權值即可。 - 用鄰接矩陣法存儲一個圖時,在不考慮壓縮存儲的情況下,所占用的存儲空間大小只與圖中結點個數有關,而與圖的邊數無關。(√)
【解析】 所謂鄰接矩陣存儲,就是用一個一維數組存儲圖中頂點的信息,用一個二維數組存儲圖中邊的信息(即各頂點之間的鄰接關系),存儲頂點之間鄰接關系的二維數組稱為鄰接矩陣。
鄰接矩陣表示法的空間復雜度為O(n2),其中n為圖的頂點數|V| - 任何無向圖都存在生成樹。(×)
【解析】 只有圖為無向連通圖時才能生成樹。多個連通分量無法構成樹 - 在用Floyd 算法求解各頂點的最短路徑時,每個表示兩點間路徑的pathk-1[I,J]一定是pathk [I,J]的子集(k=1,2,3,…,n)。
【解析】
- 拓撲排序算法適用於有向無環圖。(×)
【解析】 題內說的是“拓撲排序算法”,該算法是可以用在有向圖中來檢查是否存在環,但只有有向無環圖才能進行拓撲排序 - 只有無環有向圖才能進行拓撲排序(√)
【解析】 有環的圖是相互依賴的,所以不能。 - 對一個AOV 網,從源點到終點的路徑最長的路徑稱作關鍵路徑(×)
【解析】 AOV網的應用一般是求拓撲排序,AOE網的應用一般是求關鍵路徑 - AOE 網一定是有向無環圖
【解析】 能求出關鍵路徑的AOE網一定是有向無環圖
