數據結構基礎（八）圖Graph

今天我們就來學習“數據結構入門系列”中最后一個數據結構“圖”。圖是很常用的數據結構，比如計算機網絡、社交網絡、谷歌地圖都需要用到此數據結構，掌握圖的知識可以完善我們的數據結構知識體系，也能幫助我們解決算法中更為復雜的問題。

簡單來說，圖是一種用來表示相連數據的數據結構，類似我們的社交網絡，圖中有很多的節點，每個節點代表一個數據，每個節點可以和其他節點相連。其中每個節點叫做頂點（vertice），連接頂點之間的線叫做相連線（edge）。下圖就是一個用來表示社交網絡的圖數據結構：

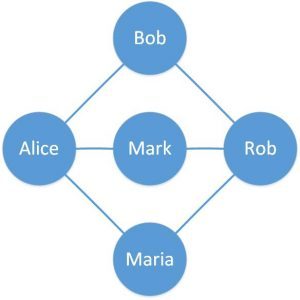
在此圖中，我們含有5個頂點和6條相連線，每個頂點包含了人名，而連接線代表相連人名之間是朋友關系。如果我們要更正式地表示圖，那么圖就可以用一對（V，E）集合來表示，其中V是一堆頂點的集合，而E是一堆相連線的集合，請看下圖：

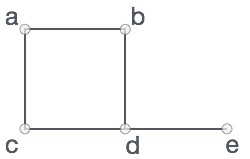
在此圖中：V = {a, b, c, d, e}，E = {ab, ac, bd, cd, de}

上面提到的圖是無向圖，而常見的圖有以下三種：

1. 無向圖（Undirected Graph）：在無向圖中，每個頂點和其他頂點通過相連線連接。
2. 有向圖（Directed Graph）：有向圖中的相連線是有方向的。
3. 權重圖（Weighted Graph）：在權重圖中，每條相連線有各自的權重。

下圖是有向圖：

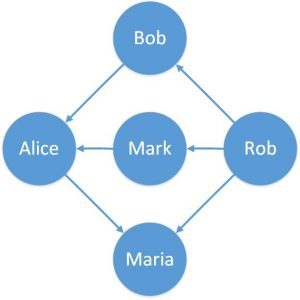
此圖可以用來表示用戶之間相互關注的情況，如果Mark指向Alice，則代表Mark關注了Alice。下圖是權重圖：

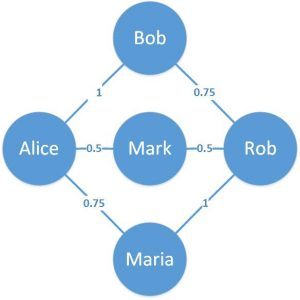
此圖可以用來表示兩個好友之間的親密程度，數值越高代表越親密。可見不同的圖可以用來表示不同的關系，而有向圖是最常見的圖，我們接下來就用Java實現有向圖。

有向圖的實現（Directed Graph）

有向圖的實現有兩種，一種是用矩陣（Matrix）的形式來實現，另一種是用鏈表（List）的形式來實現。

如果我們使用矩陣來實現有向圖，來看一個例子：

每行代表相應的頂點，如果M[i][j] = 1，那么就代表頂點 i 連向 j，如果是0，則表達頂點間沒有聯系。用矩陣的方式來實現圖的優勢很明顯，我們可以很快地判斷兩個頂點之間是否相連，可是用矩陣實現的空間復雜度很高，我們需要O(V^2)來記錄所有的數據，不管頂點之間是否有相連線。為了解決空間復雜度的問題，我們可以使用鏈表的方式來實現圖：

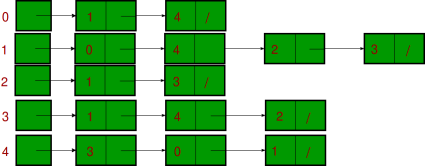
在鏈表實現中，我們實際上使用了儲存鏈表的數組來表示圖，圖的左側用數組來實現，代表我們的所有頂點，而每個頂點含有一個鏈表，鏈表上儲存了該頂點指向的頂點。以下是Java的實現代碼：

public class ListGraph {

    ArrayList<ArrayList<Integer>> graphs;

    public ListGraph(int v) {
        graphs = new ArrayList<>(v);
        for (int i = 0; i < v; i++) {
            graphs.add(new ArrayList<>());
        }
    }

    public void addEdge(int start, int end) {
        graphs.get(start).add(end);
    }

    public void removeEdge(int start, int end) {
        graphs.get(start).remove((Integer)end);
    }
}

有向圖的實現很簡單，我們直接使用Java中的ArrayList來代表左側的數組和數組上的鏈表，其中兩個重要方法addEdge和removeEdge直接使用ArrayList自帶的方法add和remove即可。使用鏈表的形式來實現圖，我們可以只記錄有用的數據，省下了很多空間。了解完圖的鏈表實現，我們來了解一下如何遍歷圖：

圖的遍歷（Graph Traversal）

遍歷圖有兩種常見的方式，一種是深度優先搜索（Depth-first Search），另一種是寬度優先搜索（Breadth-first search）。首先我們來學習深度優先搜索：

深度優先搜索（Depth-First Search）

圖的深度優先和樹的前序遍歷（Pre-order Traversal）有點類似。在深度優先遍歷中，我們假設初始狀態所有頂點都沒被訪問，然后從每一頂點v出發，先訪問該頂點，然后依次從它的各個未被訪問的鄰接點出發，深度優先遍歷圖，直到圖中所有和v相通的頂點都被訪問到。若遍歷完后，還有其他頂點沒被訪問到，則另選一個未被訪問的頂點作為起始點，重復上述過程，直到所有頂點都被訪問完為止。

下面以“有向圖”為例，來對深度優先搜索進行演示：

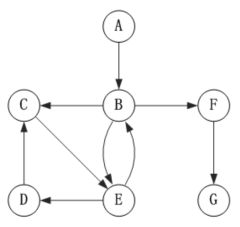
對於上面的圖，我們從頂點A開始搜索：

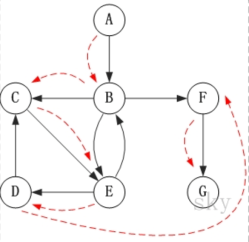
以下是具體的遍歷步驟：

1. 訪問A
2. 訪問B（在訪問A之后，接下來應該訪問的是A出發的另一個頂點，既頂點B）
3. 訪問C（在訪問B之后，接下來訪問的是從B出發的另一個頂點，既C，E，F。在此圖中，我們按照字母排序順序訪問，因此先訪問C。）
4. 訪問E（接下來訪問與C連接的另一個頂點E。）
5. 訪問D（接下來訪問從E出發的頂點B和D，因為B已被訪問過，所以訪問頂點D。）
6. 訪問F（接下來回溯“訪問A的另一個連接頂點F”）
7. 訪問G

因此訪問順序是：A -> B -> C -> E -> D -> F -> G。

在圖的深度優先搜索中，我們盡可能先遍歷一個頂點可以達到的最深處，其中可能會出現的問題就是會有循環出現，所以我們需要一個數組來記錄哪些節點已經被訪問過。以下是Java的回溯實現代碼：

public class GraphTraversal {

    ListGraph graph;
    boolean[] visited;

    public GraphTraversal(ListGraph listGraph) {
        this.graph = listGraph;
        visited = new boolean[listGraph.graphs.size()];
    }

    public void DFSTraversal(int v) {
        if(visited[v]) return;
        visited[v] = true;
        System.out.print(v + " -> ");
        Iterator<Integer> neighbors = graph.graphs.get(v).listIterator();
        while (neighbors.hasNext()) {
            int nextNode = neighbors.next();
            if (!visited[nextNode]) {
                DFSTraversal(nextNode);
            }
        }
    }
    
    public void DFS() {
        for (int i = 0; i < graph.graphs.size(); i++) {
            if (!visited[i]) {
                DFSTraversal(i);
            }
        }
    }
}

廣度優先搜索（Breadth-First Search)

廣度優先搜索算法也叫做“寬度優先搜索”或“橫向優先搜索”，其方法是從圖中的某一頂點v出發，在訪問了v之后依次訪問v的各個沒有訪問到的鄰接點，然后分別從這些鄰接點出發依次訪問他們的鄰接點，使得先被訪問的頂點的鄰接點先與后被訪問頂點的鄰接點被訪問，直到圖中所有已被訪問的頂點的鄰接點都被訪問到。如果此時圖中尚有頂點未被訪問，則需要另選一個未曾被訪問到的頂點作為新的起始點，重復上述過程，直至圖中所有頂點都被訪問到為止。換句話說，廣度優先搜索遍歷圖的過程是以v為起點，由近至遠，依次訪問和v有路徑相通且路徑長度為1，2，…的頂點。

下面以“有向圖”為例，對廣度優先搜索進行演示：

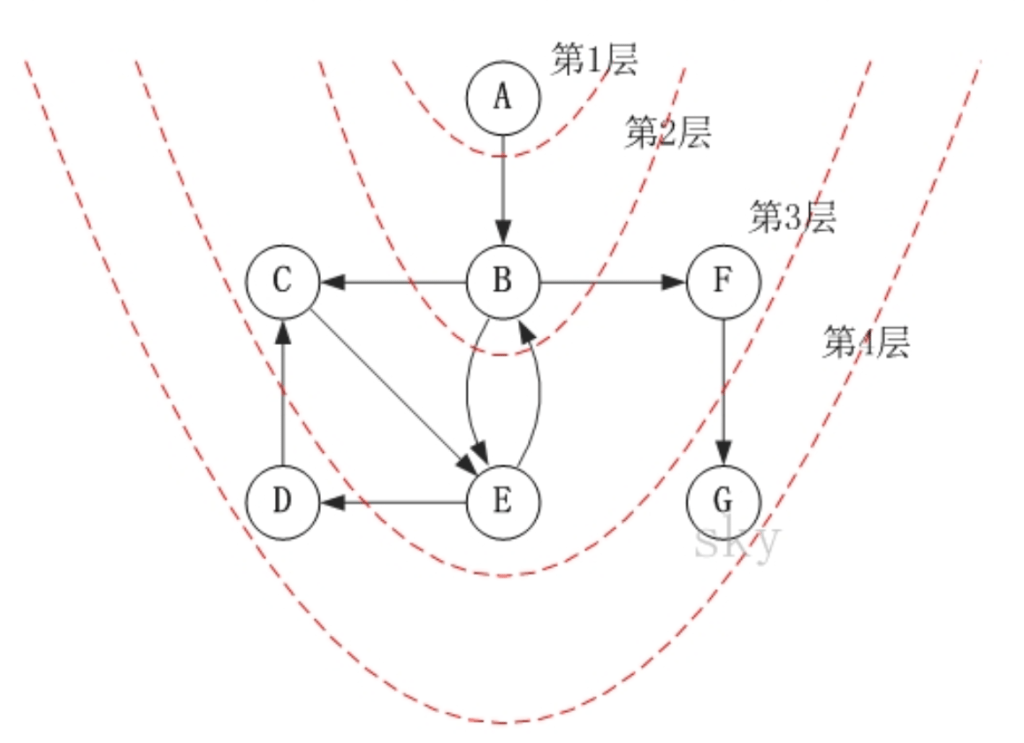
以下是訪問步驟：

1. 訪問A
2. 訪問B
3. 依次訪問C，E，F（在B被訪問之后，接下來訪問B的鄰接點，既C，E，F。）
4. 依次訪問D，G（在訪問完C，E，F之后，再依次訪問他們出發的另一個頂點。還是按照C，E，F的順序訪問，C的已經全部訪問過了，那么就只剩下E，E；先訪問E的鄰接點D，再訪問F的鄰接點G。

訪問順序是：A -> B -> C -> E -> F -> D -> G。

在實現中，我們需要使用queue來儲存接下來要遍歷的頂點（每層的鄰接點），在Java中我們通過Deque來實現Queue，以下是代碼：

public void BFSTraversal(int v) {
    Deque<Integer> queue = new ArrayDeque<>();
    visited[v] = true;
    queue.offerFirst(v);
    while (queue.size() != 0) {
        Integer cur = queue.pollFirst();
        System.out.print(cur + " -> ");
        Iterator<Integer> neighbors = graph.graphs.get(cur).listIterator();
        while (neighbors.hasNext()) {
            int nextNode = neighbors.next();
            if (!visited[nextNode]) {
                visited[nextNode] = true;
                queue.offerLast(nextNode);
            }
        }
    }
}

public void BFS() {
    for (int i = 0; i < graph.graphs.size(); i++) {
        if (!visited[i]) {
            BFSTraversal(i);
        }
    }
}

以上就是圖的兩種遍歷方法：深度優先遍歷和廣度優先遍歷。簡單來說，深度優先遍歷就是選擇一條路徑走到頭再回來，而廣度深度優先就是將最近的鄰接點先訪問完，再向更遠的頂點延伸。

Leetcode相關題目和源代碼

Leetcode題目

• Island Perimeter (463)
• Number of Islands (200)
• Max Area of Island (695)
• Number of Closed Islands (1254)
• Rotting Oranges (994)
• Sliding Puzzle (773)

GitHub源代碼

• GitHub源代碼