從一個最簡單也最經典問題說起:
能說一說
System.out.println( 1f == 0.999999999999f );的打印結果是什么嗎?這么寫有什么問題嗎?
對於這樣一個問題,回答結果一般也就兩種情況。
其實這個題目考察的目的簡單而明確:浮點數在計算機中是如何運算的?寫代碼時有什么要注意的?會有哪些坑?能說出這3個方面基本就可以了,但有些小伙伴可能忘記了。
那有同學會說了,考這樣一個破題目有實際意義嗎?工作中能遇到這種情況???
你別說,以前代碼走查時還真看到過這種用==來進行浮點數等值判斷的代碼,而且這種浮點數的精度問題在工作中還是有相當的概率會遇到的,一旦沒有發現,上線后往往就會出大問題,要背鍋的。。。

連《阿里巴巴Java開發手冊》中都有一條強制性規約和浮點數運算有關,所以其重視程度可見一斑:
浮點數之間的等值判斷,基本數據類型不能用==來比較,包裝數據類型不能用 equals 來判斷。
”

一些奇怪的現象
在涉及諸如float或者double這類浮點型數據處理時,偶爾總會有一些奇葩問題,從而會導致各種超出預期的現象發生,以前也舉過例子,比如:
- 條件判斷超預期
System.out.println( 1f == 0.9999999f ); // 打印:false
System.out.println( 1f == 0.99999999f ); // 打印:true ?
- 數據轉換超預期
float f = 1.1f;
double d = (double) f;
System.out.println(f); // 打印:1.1
System.out.println(d); // 打印:1.100000023841858 ?
- 基本運算超預期
System.out.println( 0.2 + 0.7 );
// 打印:0.8999999999999999 ?
- 數據自增超預期
float f2 = 84552631f;
for (int i = 0; i < 10; i++) {
System.out.println(f2);
f2++;
}
// 打印:8.4552632E7 ?
// 打印:8.4552632E7 ?
// 打印:8.4552632E7 ?
// 打印:8.4552632E7 ?
// 打印:8.4552632E7 ?
// 打印:8.4552632E7 ?
// 打印:8.4552632E7 ?
// 打印:8.4552632E7 ?
// 打印:8.4552632E7 ?
// 打印:8.4552632E7 ?
所以如果在業務代碼中一旦涉及到諸如:訂單金額、商品金額、交易值、貨幣運算等這種對精度要求很高的場景時,使用浮點數就一定要慎重了,一不注意就可能鍋從天而降了,而且排查起來有時候還挺費勁。
計算機是怎么表示小數的?
學過 《計算機組成原理》 或者類似 《計算機系統》 這些課程的小伙伴們應該都知道,浮點數在計算機中的存儲方式遵循IEEE 754 浮點數計數標准,可以表示為:
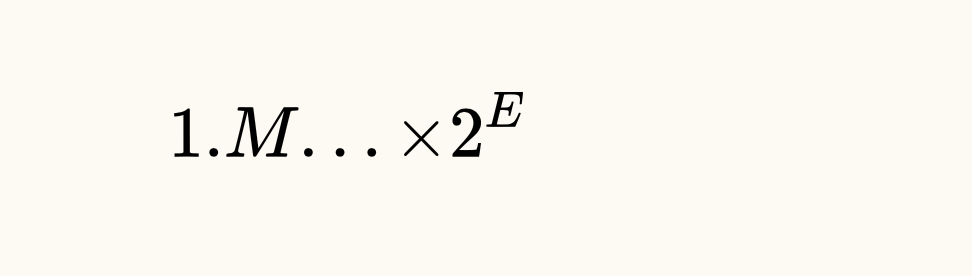
采用尾數 + 階碼的編碼方式,更通俗一點說,就是類似於數學課本上所學的科學計數法表示方式:有效數字 + 指數位!
因此,只要給出:符號(S)、階碼部分(E)、尾數部分(M) 這三個維度的信息,一個浮點數的表示就完全確定下來了,所以float和double這兩種類型的浮點數在計算機中的存儲結構就表示成下圖所示這個樣子:
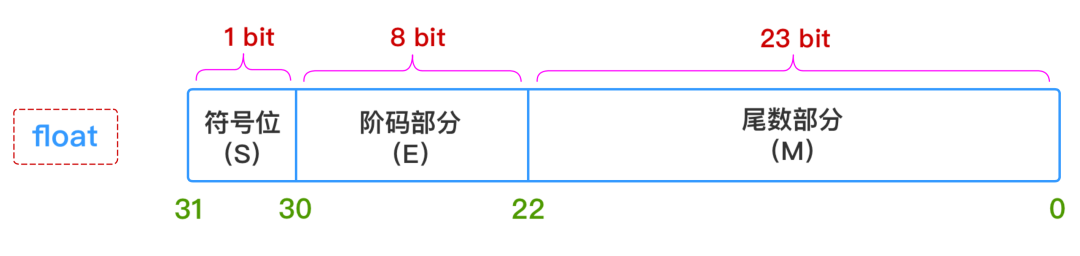
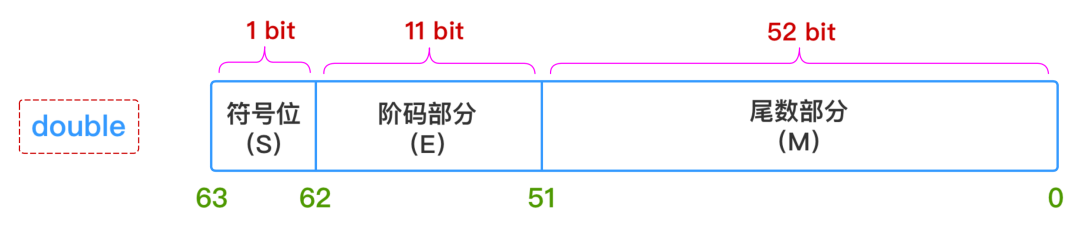
1、符號部分(S)
0-正 1-負
2、階碼部分(E)(指數部分):
- 對於
float型浮點數,指數部分8位,考慮可正可負,因此可以表示的指數范圍為-127 ~ 128 - 對於
double型浮點數,指數部分11位,考慮可正可負,因此可以表示的指數范圍為-1023 ~ 1024
3、尾數部分(M):
浮點數的精度是由尾數的位數來決定的:
- 對於
float型浮點數,尾數部分23位,換算成十進制就是2^23=8388608,所以十進制精度只有6 ~ 7位; - 對於
double型浮點數,尾數部分52位,換算成十進制就是2^52 = 4503599627370496,所以十進制精度只有15 ~ 16位
所以,浮點數交給計算機存儲的時候,可能會有精度丟失問題!!!因此使用時需要格外小心,如果真因為這一塊出了bug,定位問題還是非常艱難的,所以預防工作要做好。
小數怎么換算成二進制?
上面說的是IEEE標准規定的內容,屬於理論規約。那一個小數到底要怎么換算成二進制呢?我們得拿實際例子來解釋。
先來個簡單的例子
比如:把十進制小數0.875轉換成二進制,具體怎么操作?
可以分幾大步走:
1、以小數點為界,拆分
2、整數部分轉換
整數轉二進制我想大家應該都熟悉,使用:除2取余法 即可。而這里的0.875整數部分為0,無需操作。
3、小數部分轉換
小數部分的轉換不同於整數部分,采用的是 “乘2取整法” ,圖示一下就明白了:
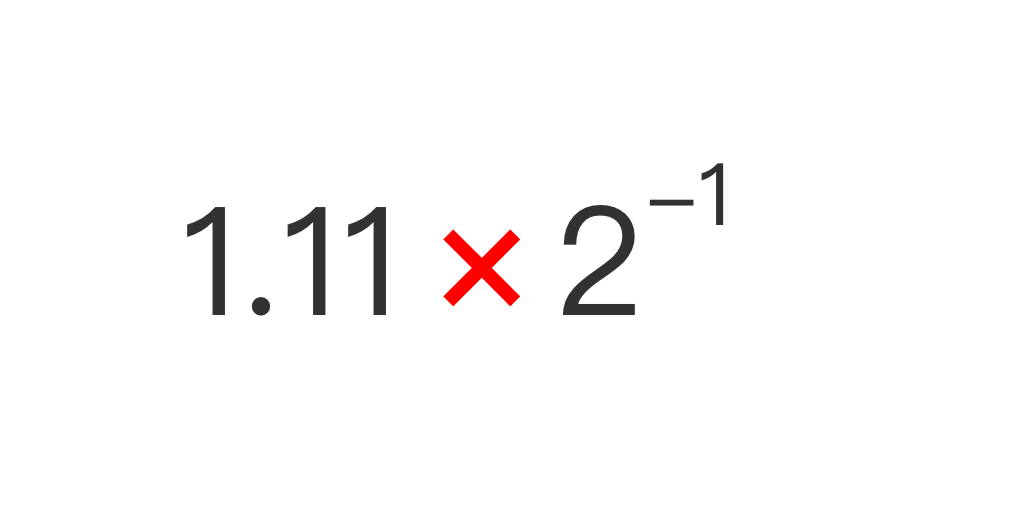
4、合並結果
整數部分 + 小數部分,最終得到二進制結果為0.111。
所以該結果按照上一節所述的尾數 + 階碼的計算機計數方式,則可以表示為:
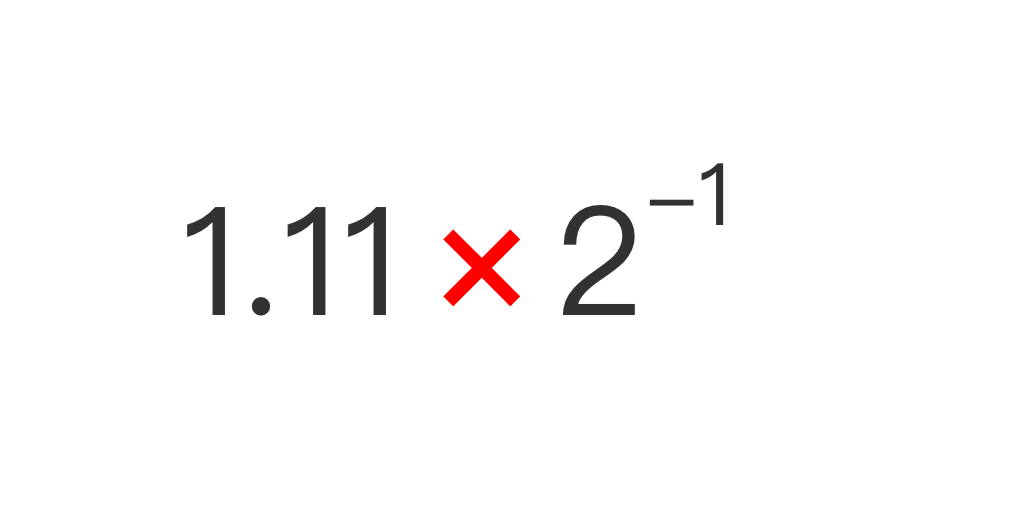
所以對應可得:
- 符號位:
0 - 階碼(E)部分:若以
float為例,應為127 +(-1)= 126,因此二進制表示為:01111110 - 尾數部分(M):若以
float為例,應為23位,因此尾部補齊后為11000000000000000000000。
因此最終的總結果為(以32位精度float表示):
00111111011000000000000000000000
再來個復雜點例子
再比如:把十進制小數6.36轉換成二進制,具體怎么操作?
但凡能用圖示,我就不想寫文字,所以用一張圖就可以解釋得明明白白:
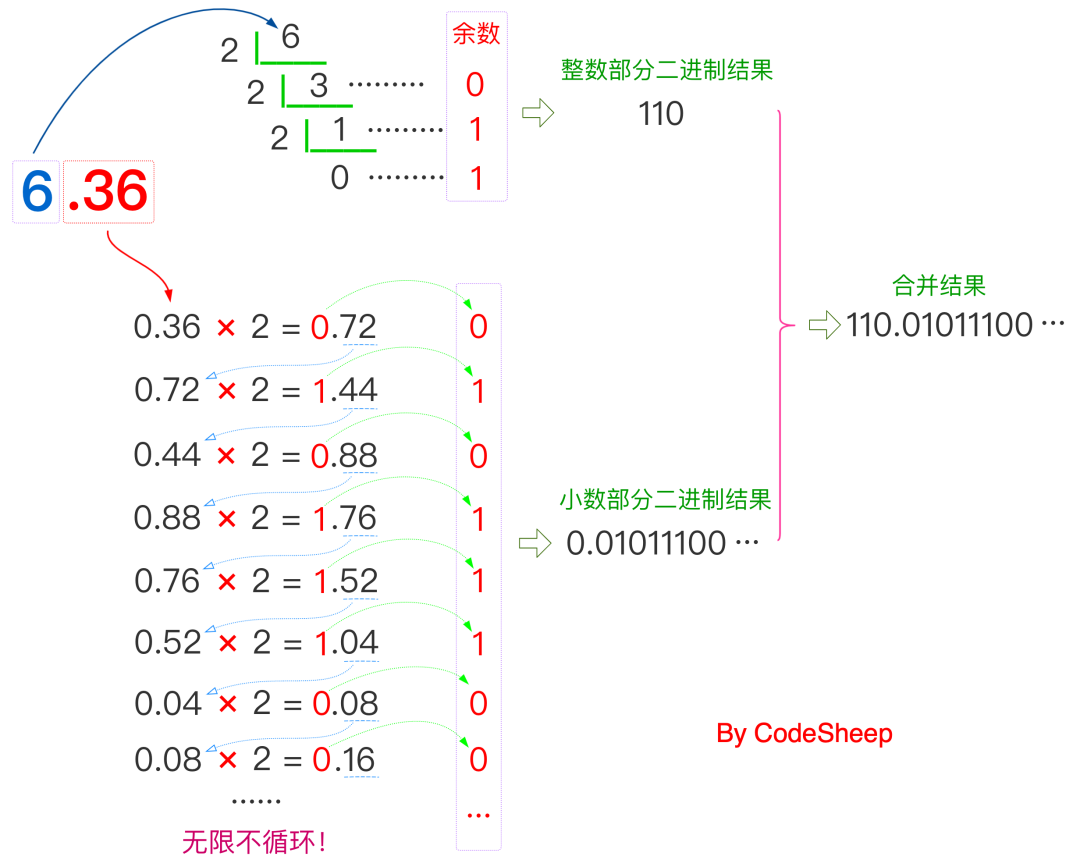
整數部分 + 小數部分,因此最終得到的結果二進制結果為110.01011100...。
還是按照上一節所述的尾數 + 階碼的計算機計數方式,則可以表示為:

所以對應可得:
- 符號位:0
- 階碼(E)部分:若以
float為例,應為127 +(2)= 129,因此二進制表示為:10000001 - 尾數部分(M):
1001011100...,但若以float型精度來截取23位,則可以表示為10010111000010100011111
因此最終的總結果為(以32位精度float表示):
01000000110010111000010100011111
因此像這種無限位數的尾數情況,用計算機存儲產生截取是必然的,必定會有一定的精度損失!這也從根本上解釋了為什么float或者double這種類型數據使用時的風險性,因此必須要結合實際業務理性考量。
所以回到文章開頭的那個問題:System.out.println( 1f == 0.999999999999f );,換算一下你就會發現,其實在float類型下,不管是1f還是0.999999999999f,它們的二進制換算結果都是:
00111111 10000000 00000000 00000000
所以結果也就不奇怪了。
binaryconvert
大家如果對上面的計算結果不放心,或者想檢查手動換算的結果是否正確,也有直接的這種二進制轉換工具站,典型的比如binaryconvert。
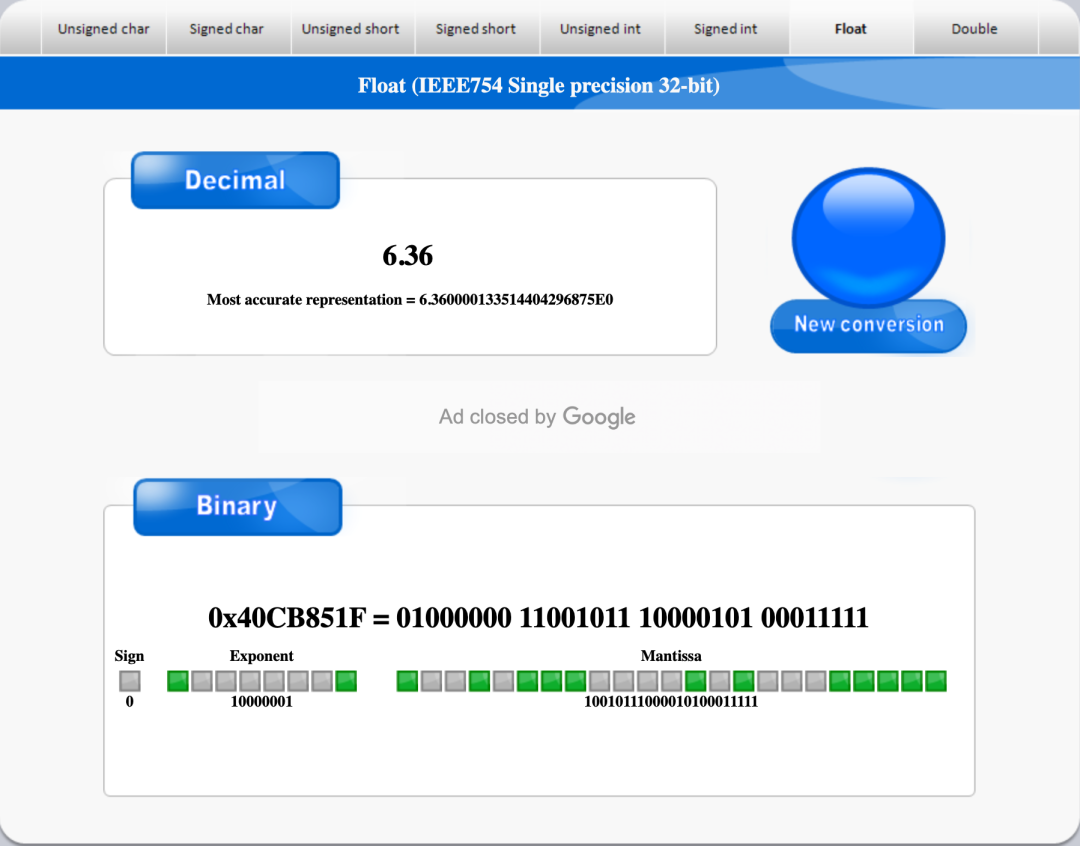
不想手動換算的,直接去上面輸入,轉換一下即可得到結果,而且可以進制互換,使用非常方便。
小 結
所以情況大致就是這樣,總之業務代碼中一旦涉及到浮點數,就得提高警惕,格外小心一些!
