本文講述了傅里葉變化的作用、基本原理以及離散傅里葉變換的使用。多圖預警，如果文字不太好理解，那么看圖也可以收獲一些東西。
傅里葉變換的作用
傅里葉變換是整個通信行業的基石，並且廣泛應用在圖像處理、音視頻處理、統計學、密碼學等等行業。
傅里葉變換的作用是什么？
打個比方，我們歷史文章有說過聲音。不同人發聲的頻率是不一樣的，男聲的頻率比較低，女聲的頻率比較高，同理尖叫頻率會非常高。
此圖上半部的橫坐標是時間，縱坐標是幅度。此圖下半部做了傅里葉變換之后的結果。
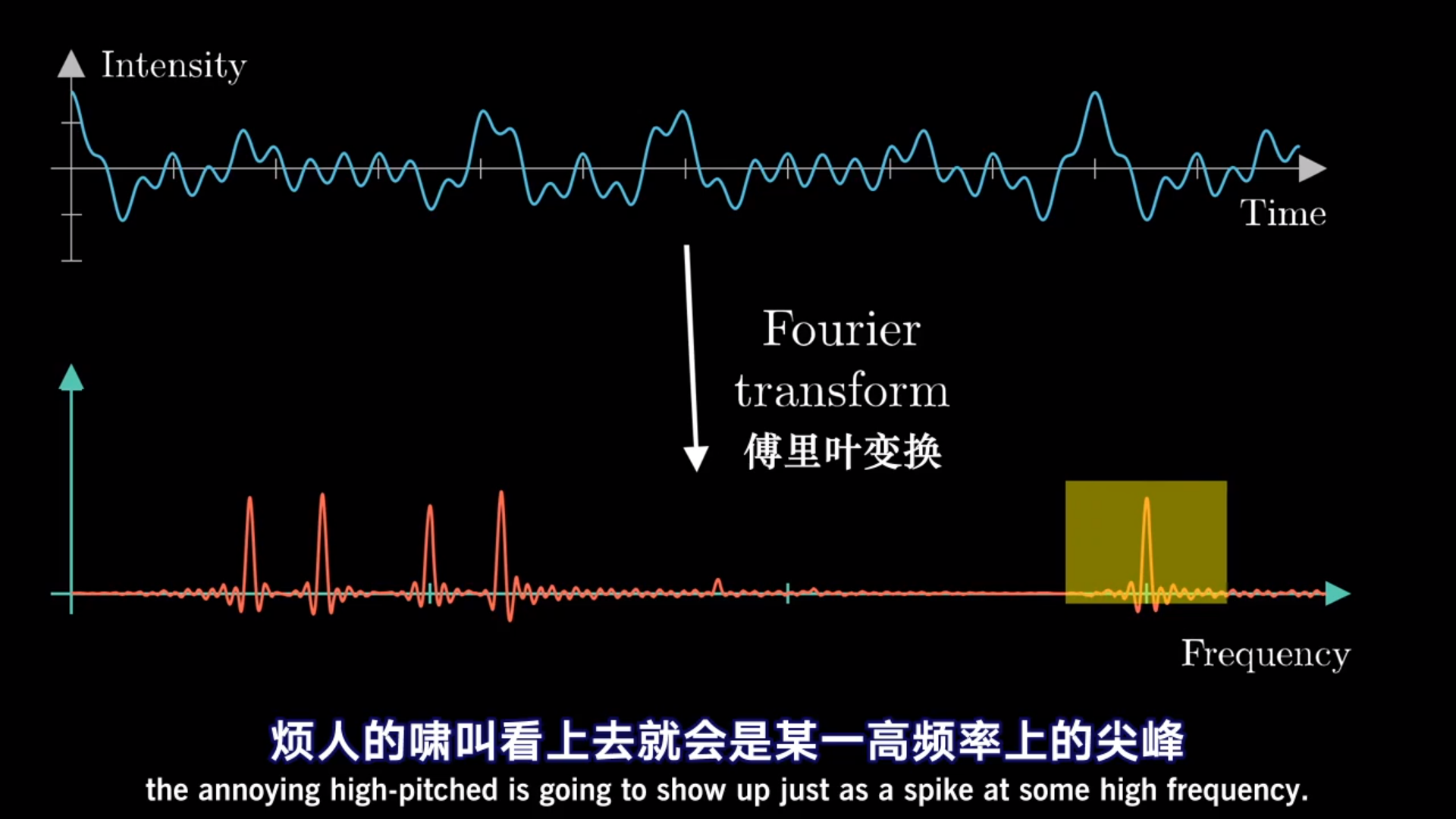
圖片源自https://www.bilibili.com/video/BV1pW411J7s8
此圖下半部分橫坐標是頻率，縱坐標是幅度，此時只需要把尖叫聲相應的頻率去掉，再做一下逆傅里葉變換，重新生成一個新的音頻，這時的音頻就沒有尖叫聲了。
圖片源自https://www.bilibili.com/video/BV1pW411J7s8
還有一個比方，就是三棱鏡。初中的時候學過，白光是由多種顏色的光組成，不同顏色的光的波長不一樣，頻率也不一樣。
聲音是波，光也是波，不同的波長的波，頻率不一樣。傅里葉變換就如三棱鏡，把不同頻率的波給分解出來。
而想要了解傅里葉變換的思想，不得不不從公式說起……
這個公式，似乎有點眼熟，甚至是不少人的痛苦回憶……
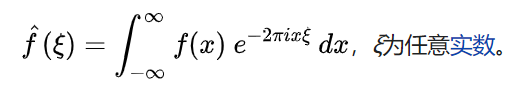
傅里葉級數
讓我們先忘了上面那個公(tong)式(ku)，不妨先假設，傅里葉一開始是這么想的(傅里葉級數的公式)：
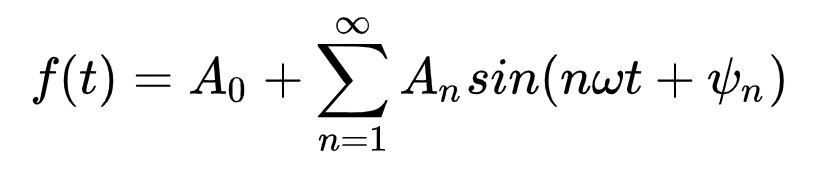
任何周期性的波形，最終都可以由一個A0的直流分量，再加上不同頻率的正弦波疊加而成。
？有點反直覺，下面這圖，演示了如何讓不同的正弦波，疊加成一個方波的：
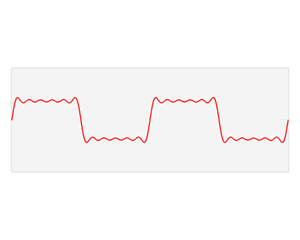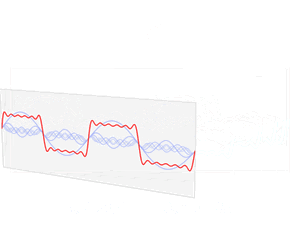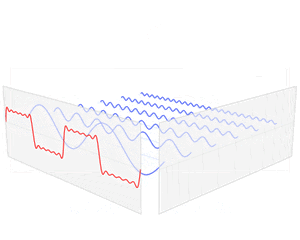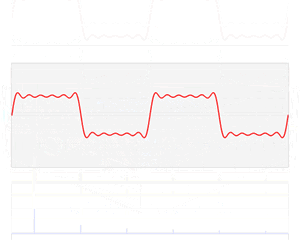
圖像來自wiki百科
又或者：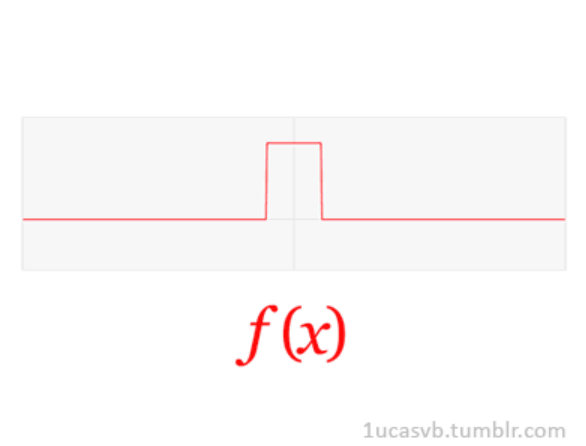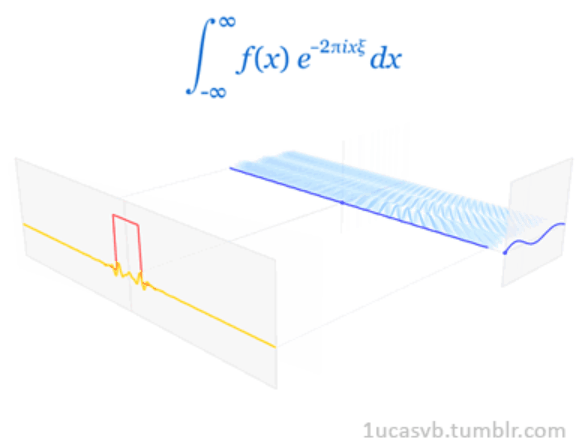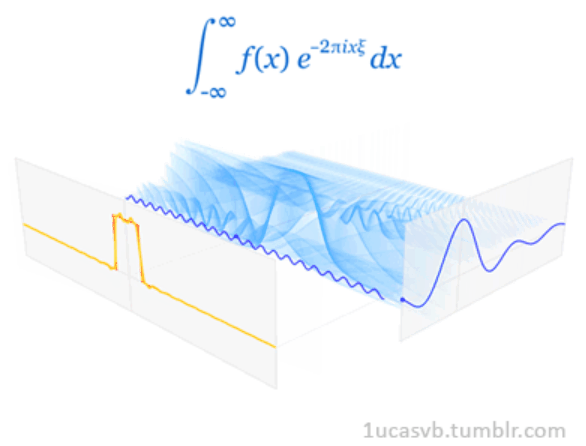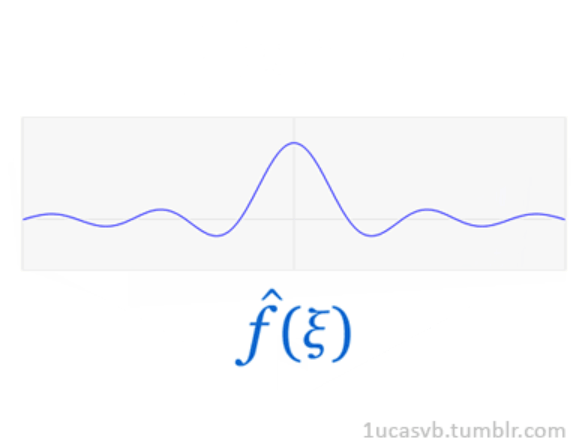 
可見只要正弦波夠多，方波就可以足夠“方”。
在數學領域，正弦波可以有無限多個，最終肯定能組成一個真正的方波。
在工程領域，由於采樣點數有限，不需要制造一個完美的方波，近似就可以了。所以是可行的。
那么問題來了，三角函數里面，我們學過sin或者cos。那么sin、正弦波到底是什么？
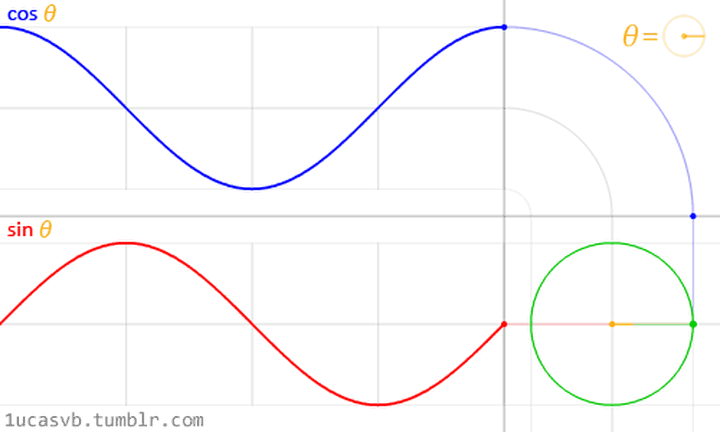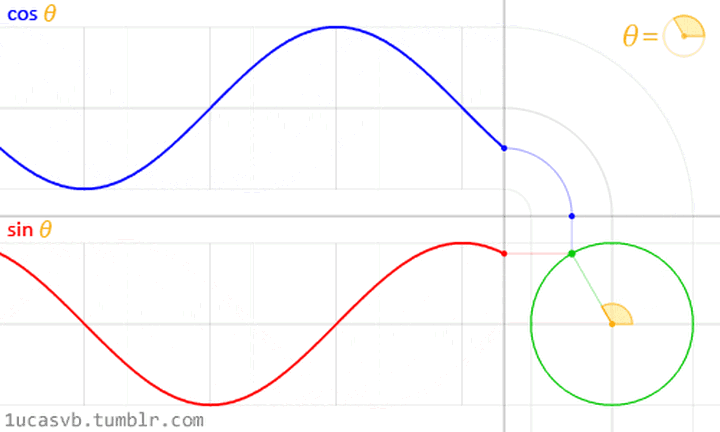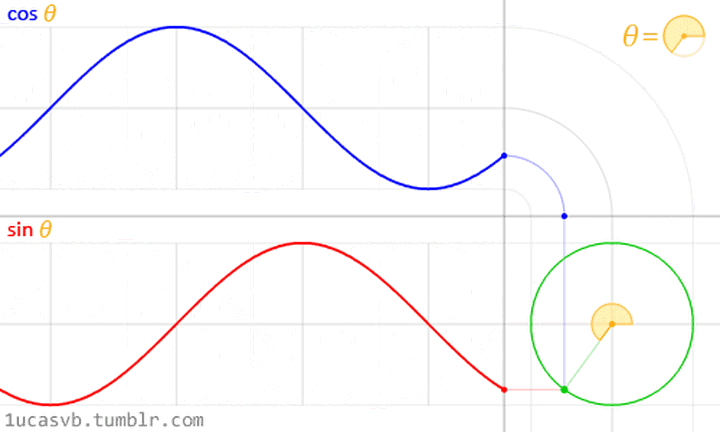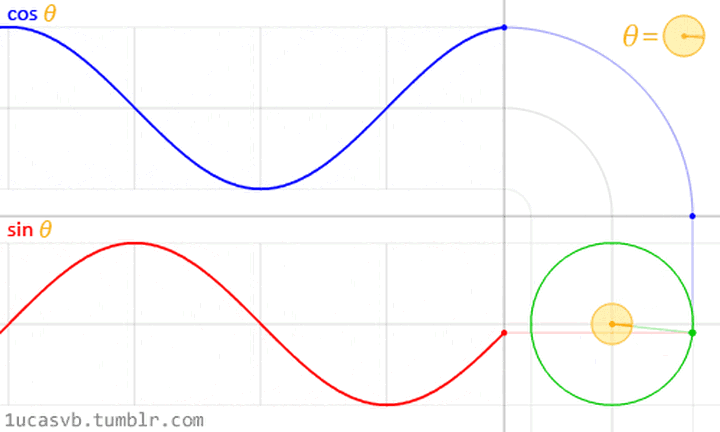
正弦信號的兩種圖形化表示 (圖片來源: http://1ucasvb.tumblr.com)
有一個長度為A的極細的木棍，一直在基於坐標原點旋轉，隨着時間旋轉，這個點在縱坐標的投影，就是sin正弦波；這個點在橫坐標的投影，就是cos余弦波。
回到這個公式，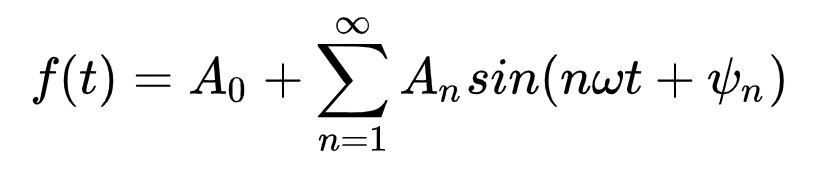
有點明白了。公式中的An是木棍的長度（幅度Amplitude），nω是這個木棍的旋轉速度（頻率Frequency），φn是木棍剛開始旋轉時的位置（相位Phase Angle）。如下圖：
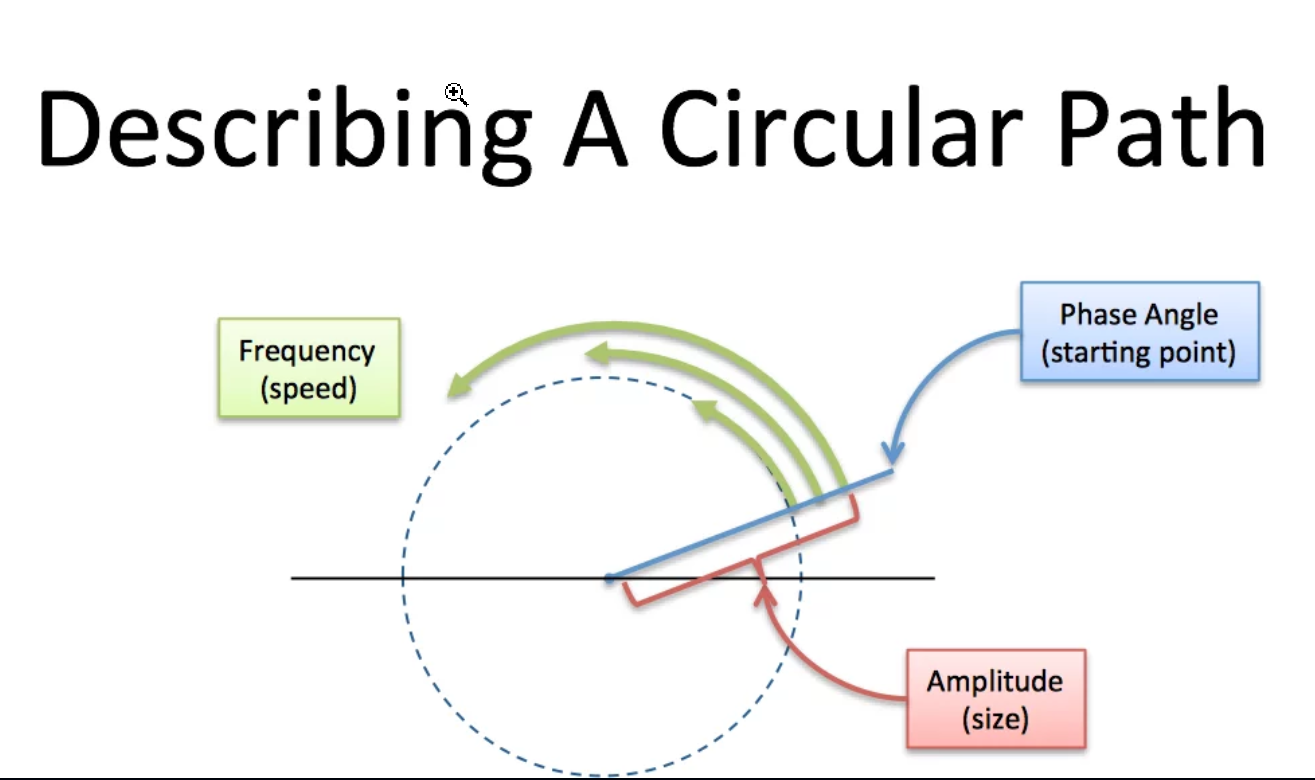
圖片源自https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
如何檢測波是否存在
如果我們想要知道，某個頻率的正弦波，是否存在於這段信號中，並且該頻率的正弦波的幅度和相位是多少。
這就利用到正弦波的正交性，正交性的一個特點是：
不同頻率的正弦波相乘，在一定周期內積分后，結果為0。
相同頻率的正弦波相乘，在一定周期內積分后，結果不為0。
那么在這段信號中，想要獲得某個頻率的正弦波的幅度和相位，檢波手段即為，該頻率的正弦波和目標信號，相乘后積分即可。
具體推導過程可以參考DBinary在zhihu上的回答 : https://www.zhihu.com/question/22085329/answer/774074211。
此刻我們需要記住的是：相乘后積分
傅里葉變換
我們知道傅里葉變換是一個神奇的頻率分離器……
剛才也說到檢波的手段是：相乘再積分……
這個時候再看看，傅里葉正變換的公式……
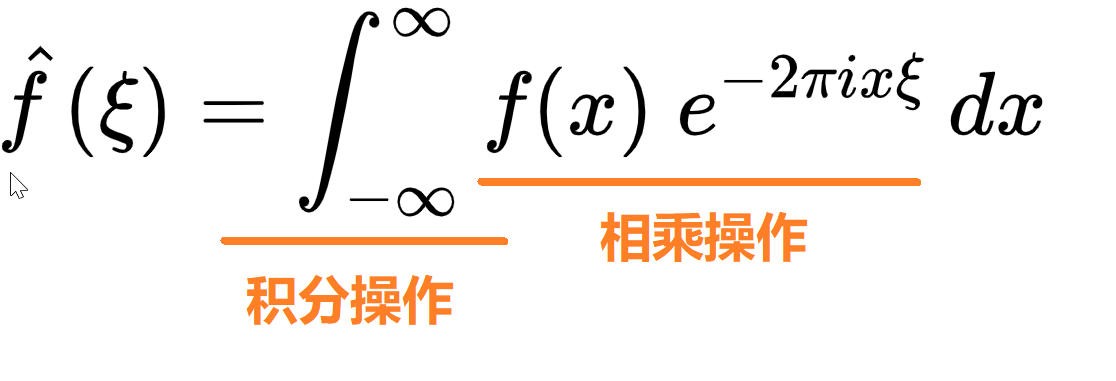
我們看到了，相乘——目標函數的相乘，也有看到了積分。
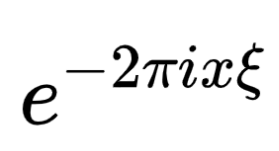
但是這個e沒看懂，難道這就代表正弦波？
沒錯，准確來講是一個復平面的正弦波。
介紹一下復平面，如下：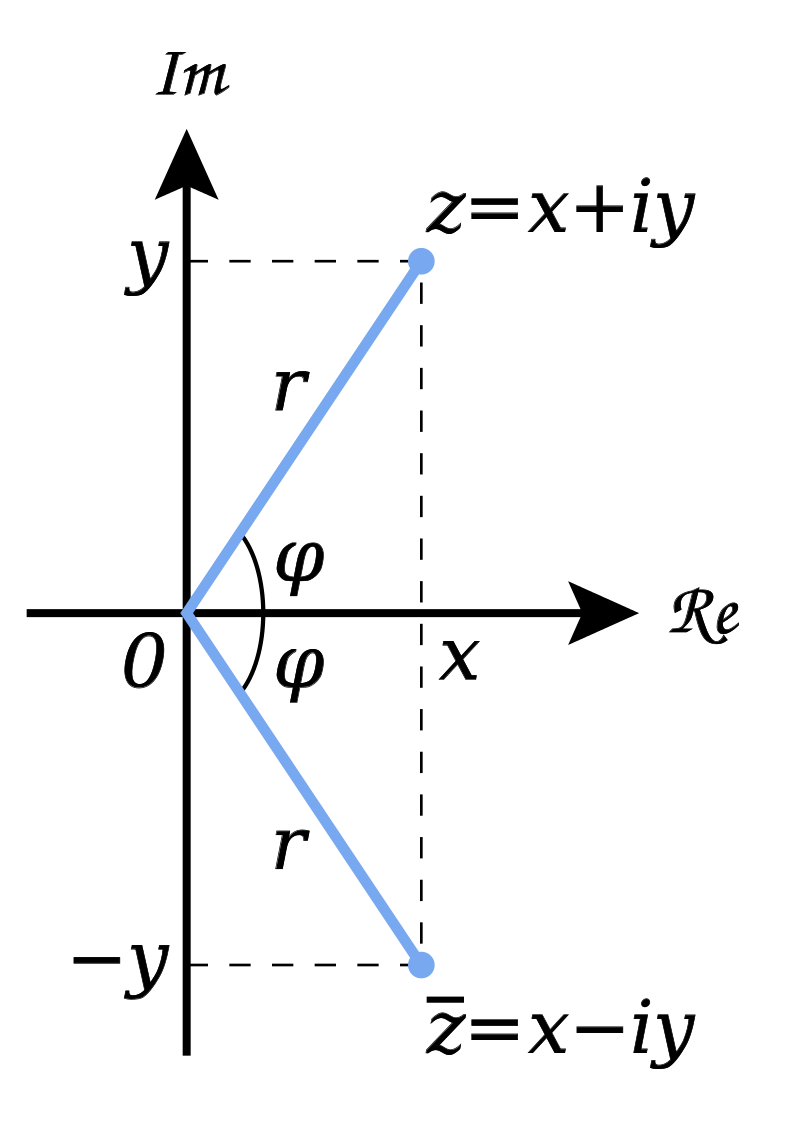 
橫軸是實軸，縱軸是虛軸。z=x+iy, z就代表：橫軸位置是x，縱軸位置是y，這樣一個向量。
還記得剛才旋轉的木棍嗎？z是一根木棍，此時此刻，我們獲得了一根靜止的木棍。
但我們得讓它旋轉起來，這樣才能得到正弦波啊。
在復數中，1乘以i，就等於i, i 再乘以 i，就是-1。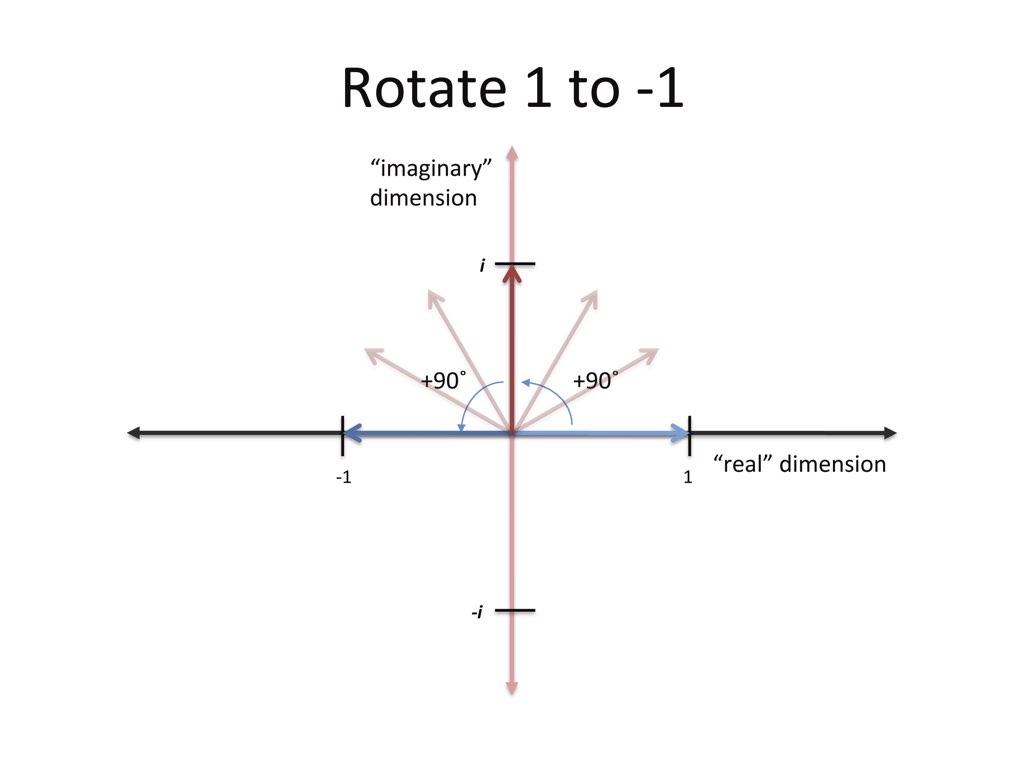 
這是因為乘以一個i，就相當於逆時針旋轉90度。
另外歐拉公式定義如下：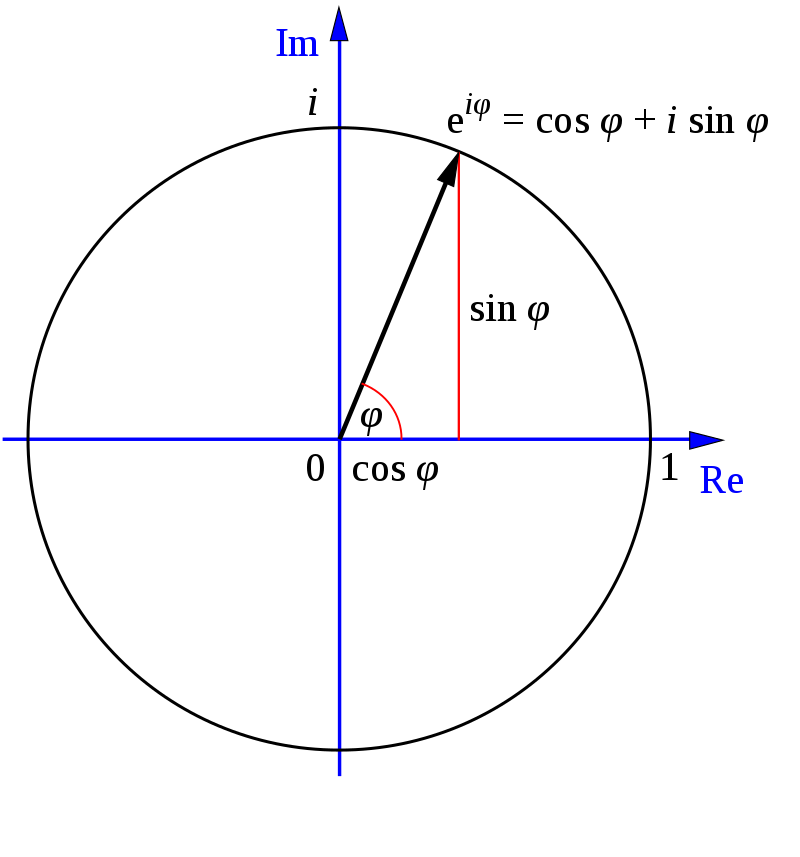 
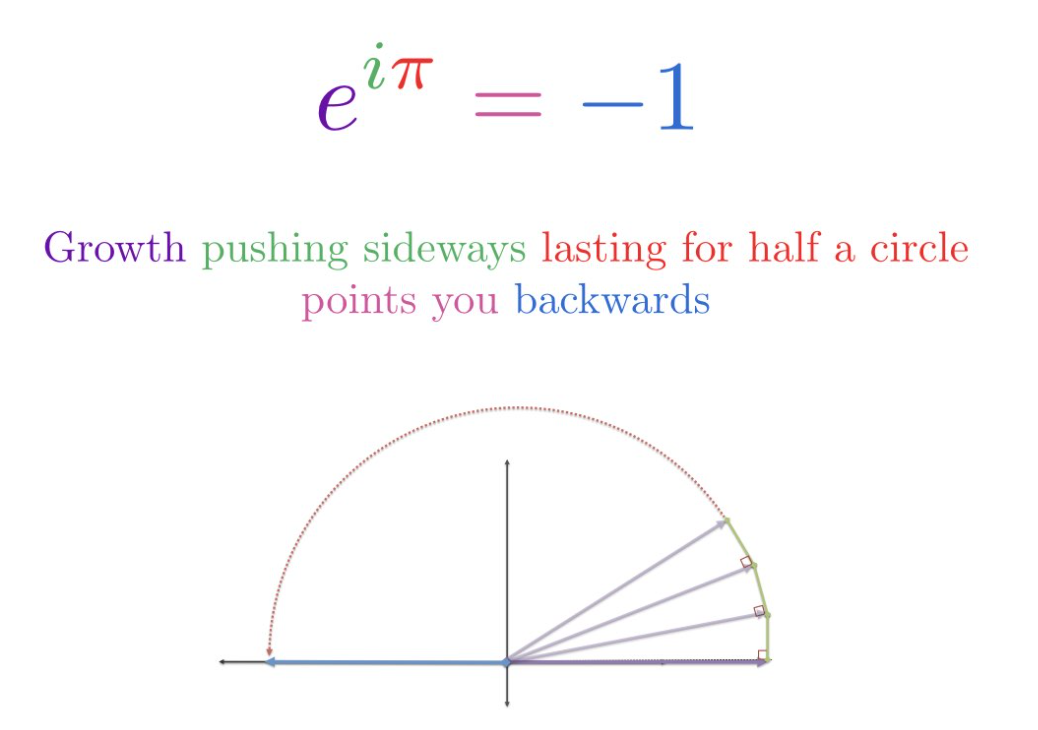
圖源自betterexplained
eiπ 代表了旋轉了180度的位置，橫坐標為-1，縱坐標為0
e2πi 代表了旋轉了360度的位置，橫坐標為1，縱坐標為0
e2πit 其中t代表時間，如果t的值是0.5秒的話，橫坐標為-1，縱坐標為0。如果t的值是1秒的話，橫坐標為1，縱坐標為0。這代表啥，代表這個木棍它隨着時間轉動了，而且轉動頻率是，一秒轉動一圈。
如果加上f這個代表頻率的變量，如e2iπft 如果此刻f是2的話，那么轉動頻率是，一秒轉動兩圈。
當然你想要讓它順時針旋轉的話，加個負號就可以了：e − 2iπft
有時候會看到，用j替代i的情況，e − 2jπft 都是一個意思，用j表示，只是因為在物理或者電子領域，i通常被表示成電流了。
也有時候 f 即頻率也會被其它字母表示（ξ），t也可能被其它字母表示，如：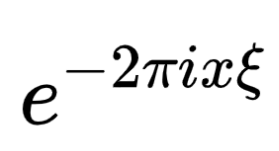
沒關系，都是一個意思。
此刻我們創建的是，正弦波的復平面信號，那么它其實是立體的，三維的。
復指數信號隨時間的變化軌跡：
復指數信號隨時間的變化軌跡，圖自《深入淺出通信原理》
復指數信號在復平面上的投影：
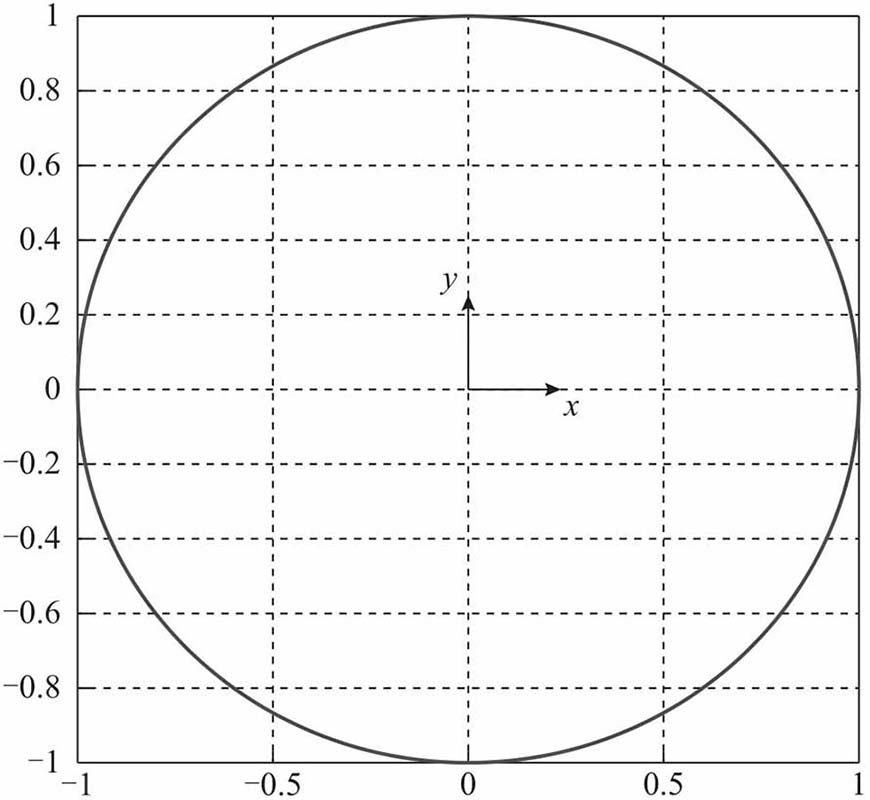
復指數信號在復平面上的投影，圖自《深入淺出通信原理》
復指數信號在實軸上的投影隨時間變化的曲線:
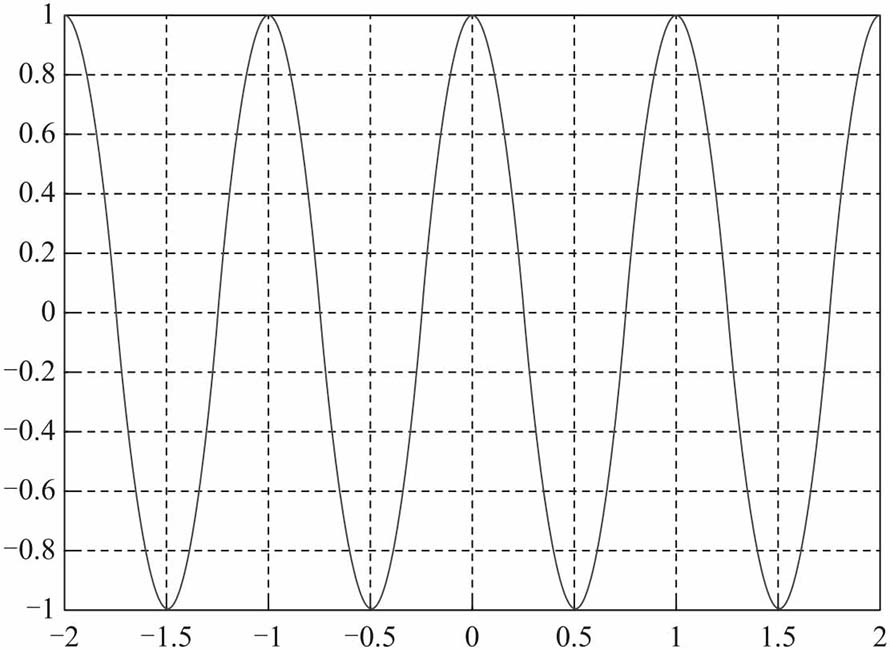
圖自《深入淺出通信原理》
復指數信號在虛軸上的投影隨時間變化的曲線:
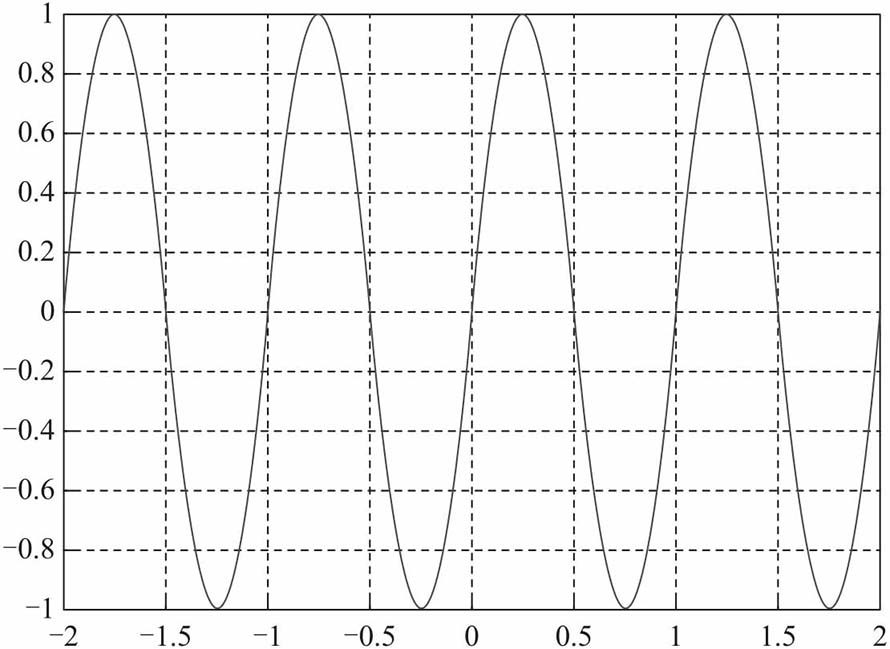
圖自《深入淺出通信原理》
如果不太好想象的話，網上有大佬做的動畫，更加直觀一點：
圖源自https://www.bilibili.com/video/av19086191/
那么問題來了，復平面信號如何和目標函數相乘。兩個復數的乘法在極坐標下的表示最簡單，笛卡爾坐標轉換到極坐標的過程: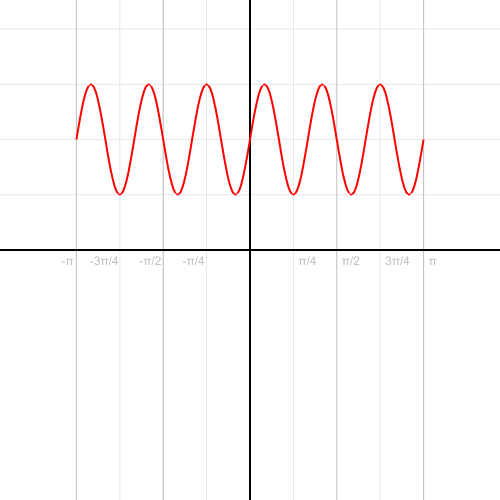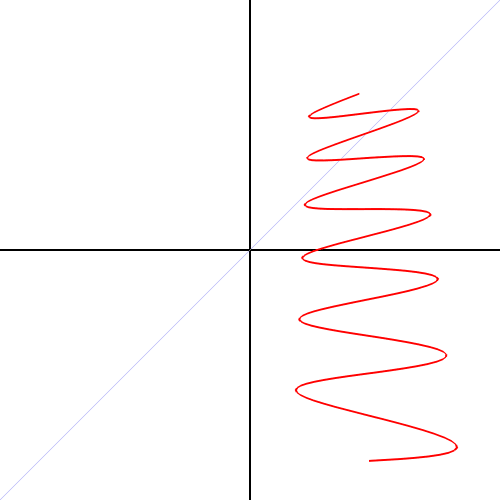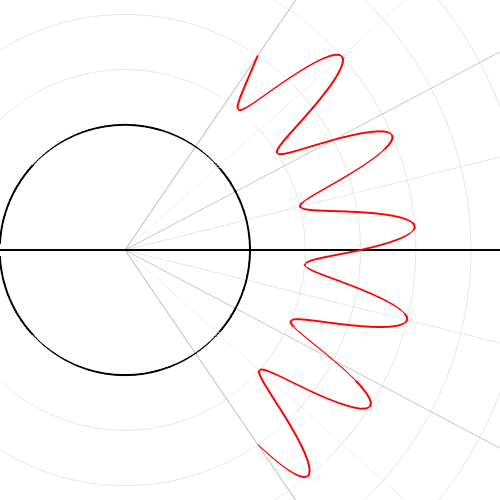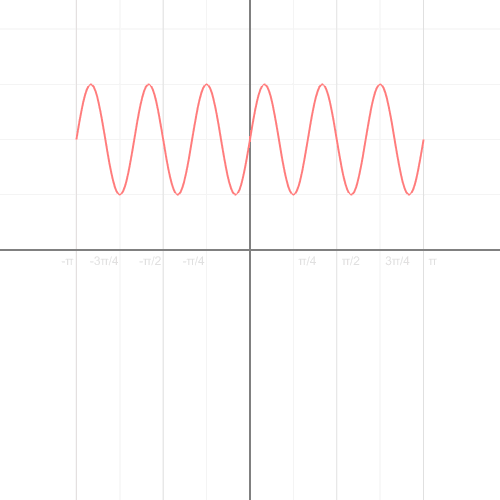 
至於相乘的過程，B站的3blue1brown的動畫，也的的確確完美地表現了出來: 
額，有點超綱了。在上一篇快速學習方法中，在學習的過程中，我們已經掌握了最小啟動知識，此刻我們需要練習，那么我們可以使用離散傅里葉變換進行練習，加深理解。
離散傅里葉變換
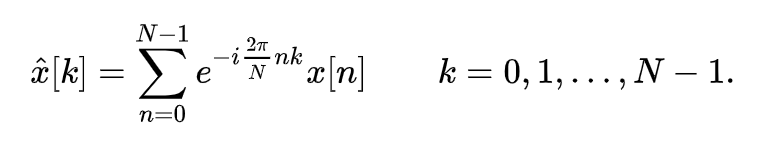
如上，相比連續傅里葉變換中的公式，以上的離散傅里葉變換中，積分變成了上面的累加，連續的頻率變化，也變成了上面的各個k個頻率的采樣。
better explained中有個吊炸天的網頁插件，可以很方便的觀察時域和頻域的變化。 : https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
因為眾所周知的牆的原因，我把這個插件下載下來，放在我的github頁面上了：https://github.com/Binfun/fourier_transform
下載打開html就可操作，如下：
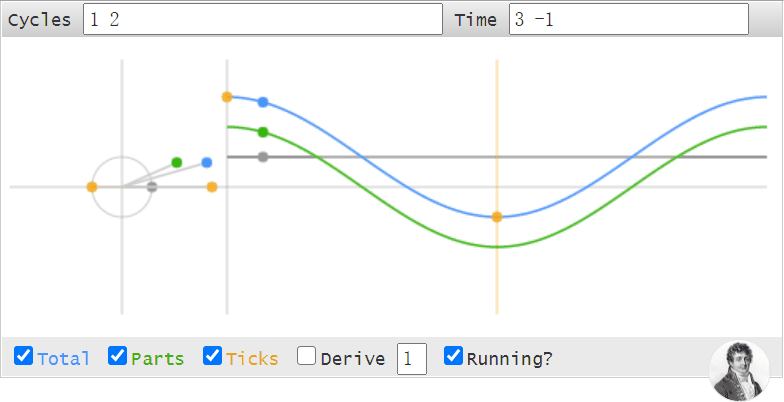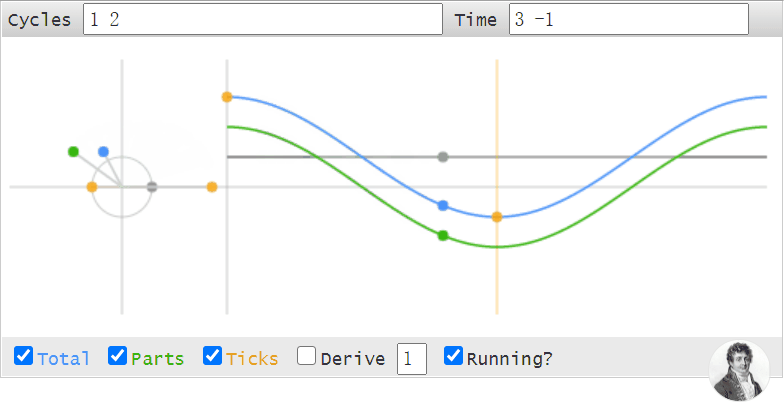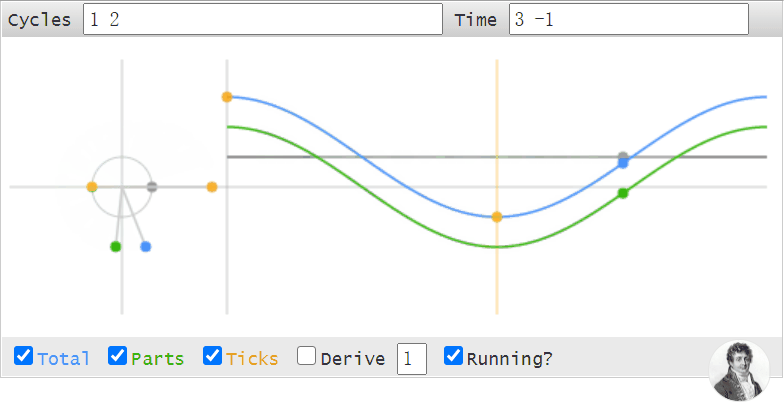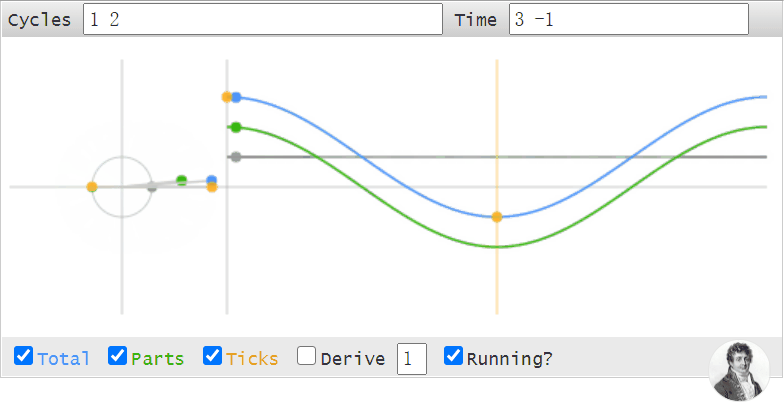
左上角的Cycles框所顯示的1 2，即為頻率數據。 右上角的Time框所顯示的3 -1，即為時域數據。
Cycles框中的第一個數字（圖中的1）即為0Hz的直流分量的幅值，
第二個數字（圖中的2）即為1Hz的正弦波的幅值，
如果有第三個數字的話，那么就代表2Hz的正弦波的幅值，以此類推3Hz 4Hz...等等。
Time框中的3 -1分別代表第1個和第2個采樣點的值，即黃色的點。
灰色的直線代表0Hz的直流分量，綠色的曲線代表1Hz的正弦波，藍色的曲線代表他們疊加的結果。
我們可以用這個工具做很多事情，比如我們可以用它來觀察，為什么時域的數據移位，等同於頻域的相位變化：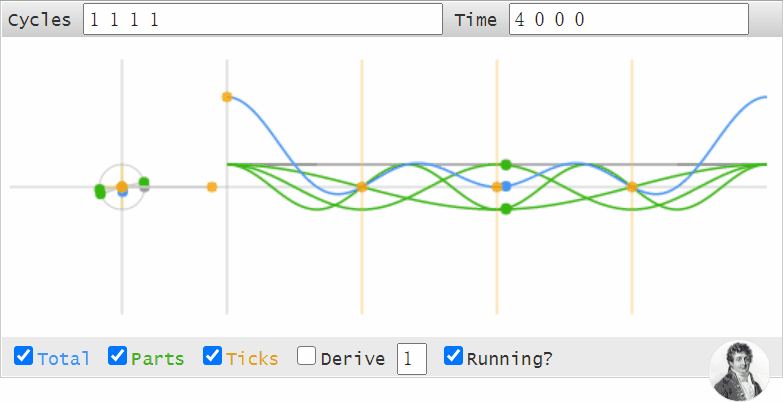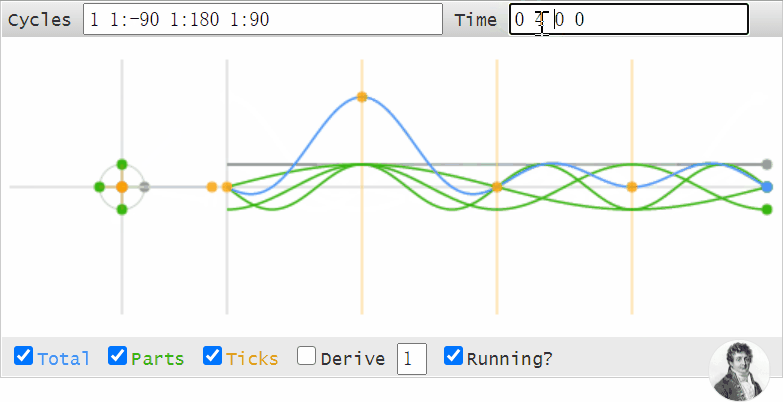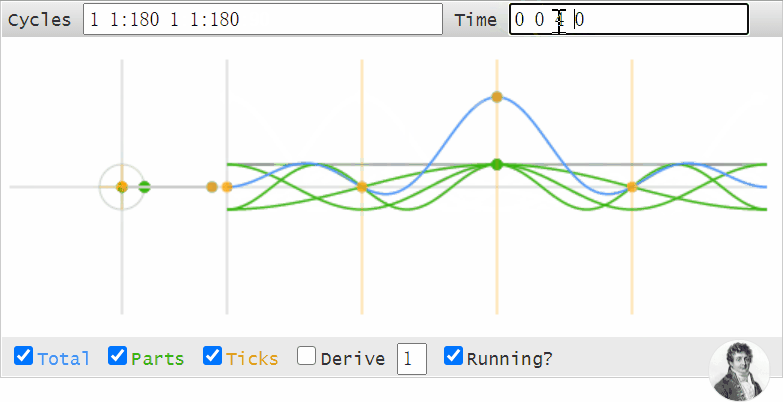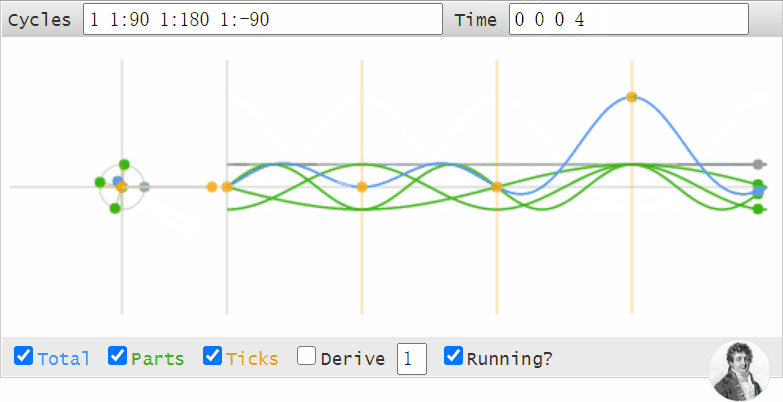 
沒錯Cycle框數字中，冒號后面的那個數字就代表相位。
甚至於，我們可以使用這段動畫去理解，觀察頻域補零，時域插值的現象：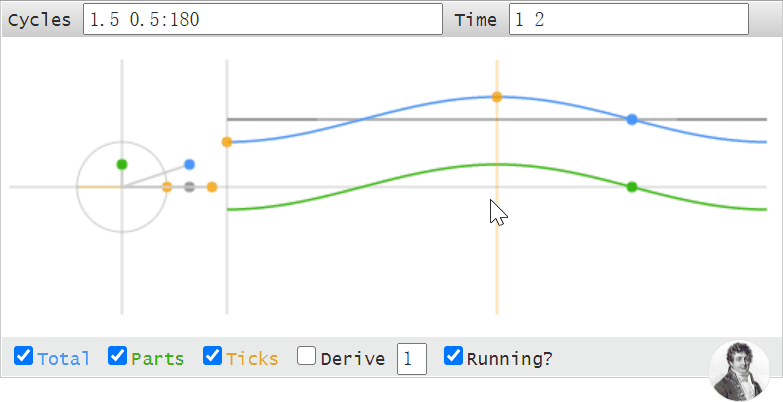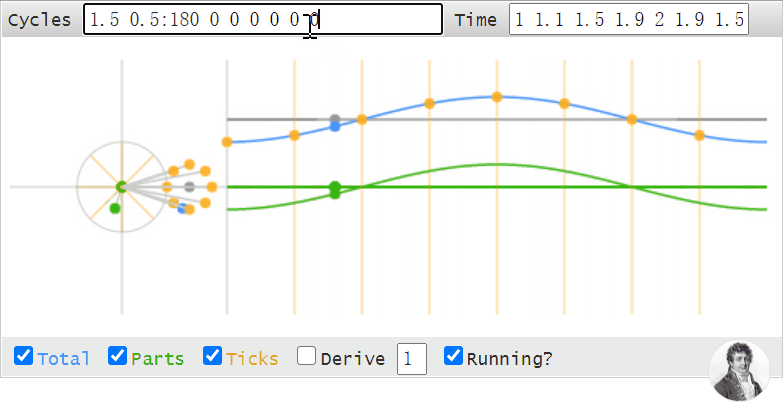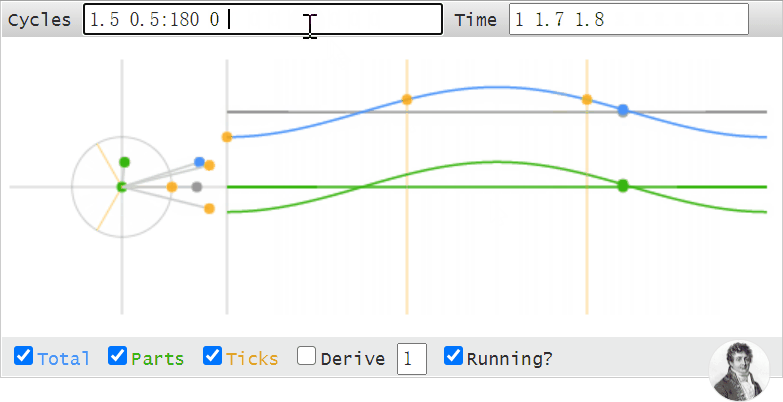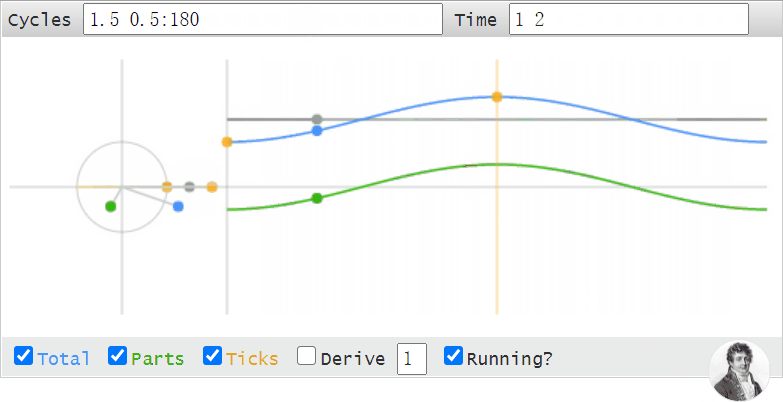 
好像說的有點遠了，強烈建議自己親手嘗試，會有不同的感覺。
回到離散傅里葉變換的公式：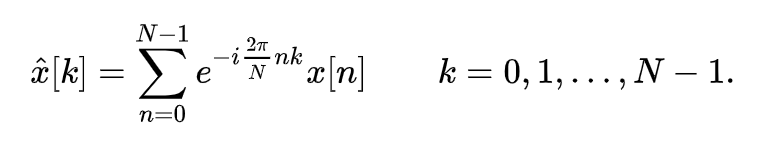
如果有時域數據: [1, 2, 3] 的話， 那么代入公式算得頻域數據的結果為:
[6 + 0i, -1.5 + 0.86603i, -1.5 - 0.86603i]
因為時域/頻域數據有3個，也就是相同頻點上累加了3次，我們需要除以N就是3，進行復原：
[2 + 0i, -0.5 + 0.28868i, -0.5 - 0.28868i]
這三個復數，就代表了下面圖中Cycles框中的：
2 0.58:150 0.58:-150
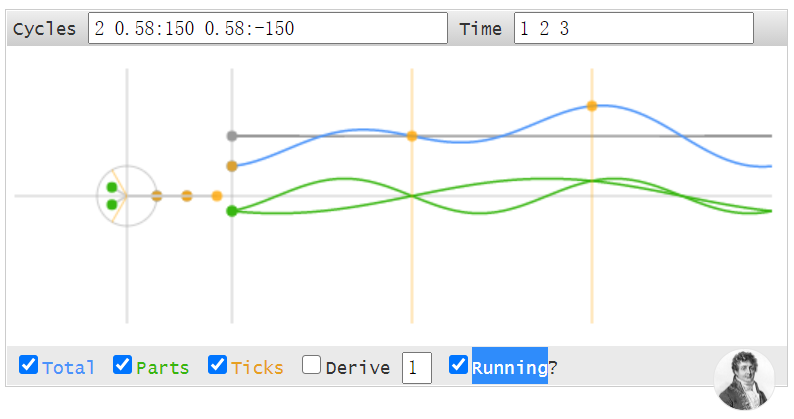
還記得上次說的那個木棍嗎？-0.5 + 0.28868i就代表旋轉速度為1Hz的木棍的起始點。
計算幅度（木棍長度）：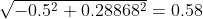
計算相位（木棍起始位置）： arctan(0.28868/-0.5) = 150度
至於代表0Hz的2 + 0i怎么理解，只有這一根木棍是不旋轉的，靜止的，是直流分量。
說道直流分量，我們就可以大膽地猜測，離散傅里葉變換，就是將時域信號當成周期信號處理，算得傅里葉級數的系數啊。
細心的同學可能發現，圖中的正弦波當相位是0的時候，其實是cos函數，而不是sin函數。
這是因為cos反應的是實數域的情況。這個頁面中，時域數據中的虛部都是0，驗證也簡單，把Cycle中的相位都加個90度試試，看看Time是不是都是0，這是因為時域的虛部的值都是0呀。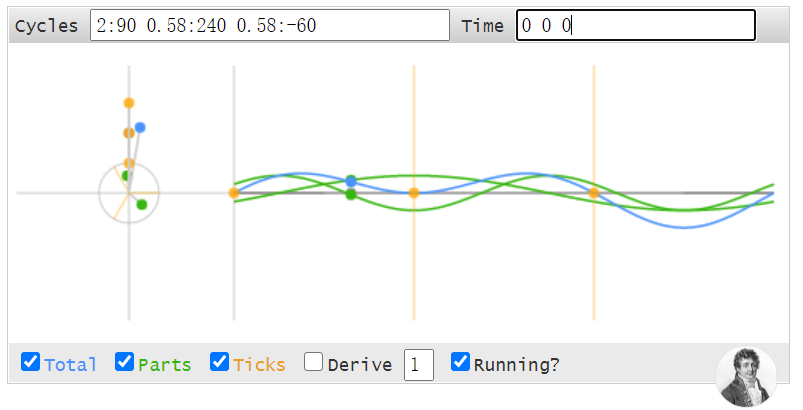 
讀到這里，可能你覺得有些細節不太夠。但也許我們已經有了點全局模糊的認識，整體框架已對，再了解細節，事半功倍。
具體細節可以參閱參考資料，巨人的肩膀，非常的精彩。
巨人的肩膀
- 直觀的數學: https://zhuanlan.zhihu.com/p/48305950
- DBinary的回答: https://www.zhihu.com/question/22085329/answer/774074211
- 傅里葉級數的推導: https://zhuanlan.zhihu.com/p/41455378
- 動圖合集: https://1ucasvb.tumblr.com/page/4
- 直觀的傅里葉變換: https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
- 3Blue1Brown出品: https://www.bilibili.com/video/BV1pW411J7s8
- 正弦波三維動畫: https://www.bilibili.com/video/av19086191/
- 陳愛軍：《深入淺出通信原理》