【學習筆記】反悔貪心

1、什么是反悔貪心？

貪心本身是沒有反悔操作的，貪心求的就是當前的最優解。但當前的最優解有可能是局部最優解，而不是全局最優解，這時候就要進行反悔操作。

另外的來自蒟蒻dalao的解釋：

眾所周知，正常的貪心算法是指在對問題求解時，總是做出在當前看來是最好的選擇。也就是說，不從整體最優上加以考慮，算法得到的是在某種意義上的局部最優解。也就是說我們的每一步都是站在當前產生的局面上所作出的最好的選擇，是沒有反悔操作的。

不加反悔的一直朝着當前局面的最優解走很可能導致我們被困在局部的最優解而無法到達全局的最優解，就好像我們爬山就只爬到了一座山的山頂卻沒有到整片山的最高處：

但是反悔貪心允許我們在發現現在不是全局最優解的情況下回退一步或若干步采取另外的策略去取得全局最優解。就好像我們站在的一座山的山峰上，看到了還有比我們現在所在位置還高的山峰，那我們現在就肯定不是在最高的地方了，這時我們就反悔——也就是下山再爬上那座更高的山：

這就是反悔貪心的大致思路。根據反悔記錄操作的不同，反悔貪心又分為反悔堆和反悔自動機。

總的來說：反悔操作指的是這一步的貪心不是全局最優解，我們就退回去一步（人工或自動判斷），換一種貪心策略。按照判斷方式的不同可以分為反悔自動機和反悔堆兩種方法。

1. 反悔自動機：

   即設計一種反悔策略，使得隨便一種貪心策略都可以得到正解。

   基本的設計思路是：每次選擇直觀上最接近全局最優解的貪心策略，若發現最優解不對，就想辦法自動支持反悔策略。（這就是自動機的意思）

   具體題目具體分析。一般需要反悔自動機的題都是通過差值巧妙達到反悔的目的。

2. 反悔堆：

   即通過堆（大根堆、小根堆）來維護當前貪心策略的最優解，若發現最優解不對，就退回上一步，更新最優解。

   由於堆的性質，使得堆的首數據一定是最優的，這就可以實現快速更新最優解。

2、例題以及代碼

反悔堆

用時一定模型

USACO09OPEN 工作調度Work Scheduling

Description:

有 \(n\) 項工作，每 ii 項工作有一個截止時間 \(D_i\) ，完成每項工作可以得到利潤 \(P_i\) ，求最大可以得到多少利潤。

Method:

盡管這道題直接理解會感覺簡單，實則不然。

對於簡單貪心：

第一種貪心是開一個桶，對於每一個截止日期我們都只保留能產生價值最大的任務去做，其余的不去做。這種方法很明顯是錯誤的，我們可以舉出一個例子來否定這個策略。比如我們只有兩個任務A和B，A任務的截止日期是3，價值是3；B的截止日期是3，價值是1。按照我們的貪心策略，我們就舍棄B選擇A，但是實際上，我們可以在時間2去做B，時間3去做A這樣就可以全都要，明顯比只做A會好得多，所以這種貪心策略是不可取的。

第二種貪心就更加明智一點，我們都有一種直覺那就是先完成比較緊急的任務亦或者說先完成截止日期靠前的任務會更加優。所以我們就按照截止日期(從小到大)為第一關鍵字，價值(從大到小)為第二關鍵字進行排序，然后順序遍歷每個任務，能做就做，不能做(當前已安排任務數=當前任務的截止日期)就直接拋棄。這樣做看起來很有道理，但實際上有有可能到后期都是高報酬的工作（但由於前期做了太多價值很低的任務導致都超時做不了了）就會讓答案不是很優秀。比如我們舉個例子。加入我們有四個任務A、B、C、D.其中A任務的截止日期為1，價值為2；B的截止日期為1，價值為1；C的截止日期為2，價值為5；D的截止日期為2，價值為6。按照我們現在的貪心策略，我們會排序后按照ABDC的順序進行考慮，然后選擇AD這兩個任務去完成最后結果是8。但實際上，如果我們不去做A，而是把做A的時間拿去做C，這樣我們最后的結果就是11是優於我們的貪心答案的。

為什么會出現這樣的問題呢？是因為到了后期，我們見到了很多高回報的工作但是能做的卻很有限了，這又是因為前期做了很多價值很低的任務，換句話說我們可能會后悔前期做了些低報酬的工作。那我們能不能反悔，也就是退掉之前低報酬的工作用那個時間去完成高報酬的工作呢？這就要用到我們的反悔堆。

當然我們還有第三種貪心，以價值為關鍵字從大到小排序，假如我們考慮第i個任務做不做，如果從1∼t[i]（第i個任務的截止時間） 沒有塞滿，那就盡量咕到最后一個空位做，正確也是顯然的，但是直接暴力是 \(O(n^2)\) 的。然后我們發現找空位的過程可以優化，加入樹狀數組，二分位置判斷即可，時間復雜度 \(O(nlog^2n)\) 即可以通過。

反悔貪心：

假如滿足題設條件（即沒有超出截止時間）就分成兩種情況：若當前的最優解比原來的最優解（堆頂）更優秀，我們就更新全局最優解，把原來的最優解丟出去，再把當前的最優解放進去（即反悔策略）；反之，就不管了。假如不滿足特設條件，就把當前的最優解丟進堆里，更新全局最優解即可。

// RioTian 21/03/10 學習自 蒟蒻dalao
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
struct node {
    int deadline, value;
    //重載<號的定義，規定堆為關於價值的小根堆
    bool operator<(const node &v) const {
        if (value > v.value) return true;
        return false;
    }
} a[110000];
// 使用優先隊列代替手寫堆(節省Coding時間)
priority_queue<node> q;
int n;
ll ans = 0;

//自定義排序函數，將任務按截止時間從小到大排序
bool cmp(node x, node y) {
    if (x.deadline < y.deadline) return true;
    return false;
}

int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i].deadline >> a[i].value;
    sort(a + 1, a + 1 + n, cmp);
    for (int i = 1; i <= n; ++i) {
        //如果當前決定做的任務數小於截止日期也就是還有時間做當前任務
        if (a[i].deadline > q.size()) {
            ans += a[i].value;
            q.push(a[i]);
        } else {
            if (a[i].value > q.top().value) {
                ans -= q.top().value;
                q.pop();
                q.push(a[i]), ans += a[i].value;
            }//反悔操作 
        }//考慮是否反悔，不做之前做的任務 
    }
    cout << ans << "\n";
    return 0;
}

價值一定模型

模型總結來自蒟蒻dalao，萬分感謝！

Description:

我們再來考慮這樣一個問題，我們有 \(n\) 個任務( \(n≤1e5\) )，並且每個任務都有兩個屬性——截止日期和完成耗時。在截止日期前完成任務就可以得到這個任務產生的價值。在同一時間我們只能去做一個任務。所有任務的價值都是一樣的，問我們最后最多能完成多少個任務。

算法講解

有了剛剛那題的基礎，我們也很容易可以考慮到反悔貪心的反悔堆模型上。由於我們需要反悔操作，而反悔操作是建立我們能夠反悔——不做之前決定做的任務而去做當今決定做的任務，所以首先我們肯定還是要按照截止日期從小到大進行排序。

在我們上面講到的用時一定的模型中，我們用堆維護“性價比”最低的任務也就是我們價值最低的任務用於反悔操作。在這個問題中，我們同樣用堆去維護“性價比”最低的任務。由於每個任務的價值是一定的，所以我們性價比最低的任務就是耗時最長的任務，如果我們不做耗時比較長的任務去做耗時比較短的任務，我們就能留下更多的時間給后面的任務，又由於每個任務的價值是一樣的，所以這樣做的正確性也是顯然的。

所以具體來說我們就開一個大根堆維護已選任務的時間，堆頂就是耗時最長的任務。我們順次考慮排序后的每個任務，當前決定要做的任務的總耗時加上現在這個任務的耗時小於等於現在這個任務的截止時間，那我們就直接做，把現在這個任務丟進堆里，總耗時加上現在這個任務的耗時就可以了。但如果當前決定要做的任務的總耗時加上現在這個任務的耗時大於現在這個任務的截止時間呢，我們就考慮是否進行反悔操作替換決定做的任務。我們看一看堆頂任務的耗時和現在這個任務的耗時，如果堆頂任務的小那就不替換；如果當前任務的耗時小，我們就用當前任務替換掉堆頂任務就好啦。

模板代碼

這道題也是有模板題的，題目是[JSOI2007]建築搶修，下面附上模板代碼：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
struct node {
    int deadline, time;
    //重載<號的定義，規定堆為關於耗時的大根堆
    bool operator<(const node &v) const {
        if (time < v.time) return true;
        return false;
    }
} a[160000];
// 使用優先隊列代替手寫堆(節省Coding時間)
priority_queue<node> q;
int n;
ll last = 0;

//自定義排序函數，將任務按截止時間從小到大排序
bool cmp(node x, node y) {
    if (x.deadline < y.deadline) return true;
    return false;
}

int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i].time >> a[i].deadline;
    sort(a + 1, a + 1 + n, cmp);
    for (int i = 1; i <= n; ++i) {
        //如果決定做的任務耗總時加上當前任務耗時小於等於當前任務截止時間
        if (a[i].deadline >= last + a[i].time) {
            last += a[i].time;
            q.push(a[i]);
        } else {
            //如果堆頂耗時大於當前考慮任務的耗時
            if (a[i].time < q.top().time) {
                last -= q.top().time;
                q.pop();
                q.push(a[i]), last += a[i].time;
            }  //反悔操作
        }      //考慮是否反悔，不做之前做的任務
    }
    cout << q.size() << "\n";
    return 0;
}

反悔自動機

相比於反悔堆，反悔自動機更加高級一點，它能夠自動的維護我們反悔的操作，通常適用於帶限制的決策問題上。

舉例：假如我們有四個數ABCD，AB當中只能選一個，CD當中只能選一個，問我們最后能收獲的最大價值是多少。

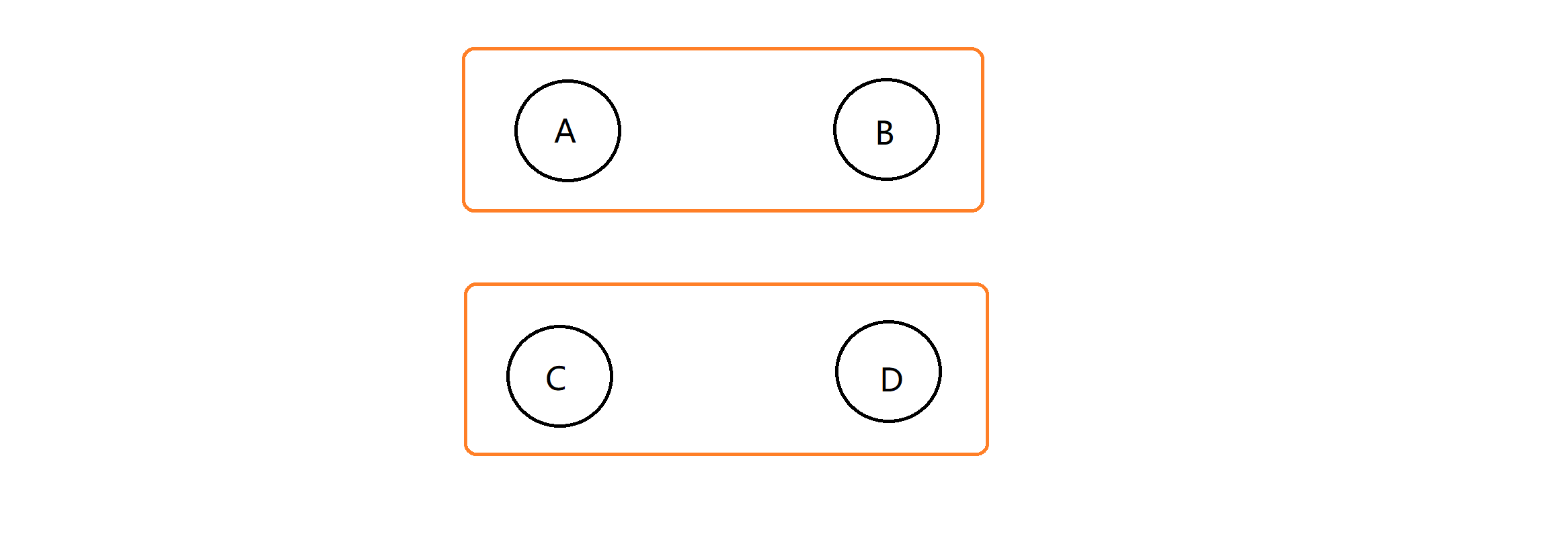
假如剛開始我們選的是AC，那我們就可以把AC先刪掉，把的值B變成B-A，D的值變成D-C，接下來的選擇不考慮任何束縛。這樣如果我們接下來再去選B，那這時我們選的值其實是B-A，加上之前選的A，相當於我們選了B沒有選A，這就完成了返回操作——通過修改關聯點的值讓我們做到不選之前決定選的點而去選現在這個點。

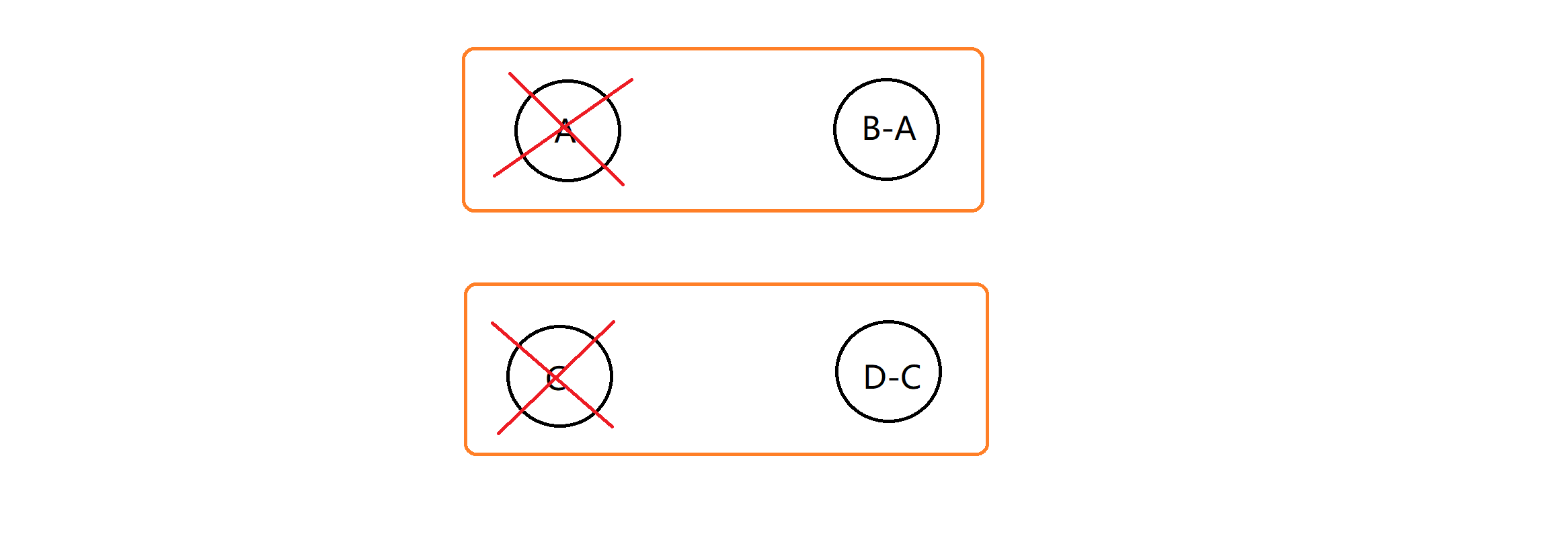
這就是反悔自動機的大致思路。具體的反悔自動機又分為堆反悔自動機和雙向鏈表反悔自動機兩種，這樣講可能有點抽象，我們下面通過幾個例題來看看反悔自動機的具體運用。

堆反悔自動機

CF865D Buy Low Sell High（堆反悔自動機）

Description:

已知接下來 \(n\) 天的股票價格，每天可以買入當天的股票，賣出已有的股票，或者什么都不做，求 \(n\) 天之后最大的利潤。

Method：

我們先從簡單的貪心開始考慮。首先我們可以貪心地對於每一天 i，如果我們可以賣出，那么貪心的選擇之前的價格最小的一天 j，然后若 \(P_j < P_i\) 就可以在 j 天買入一股，然后在第 i 天賣出，這時候就僅需要一個 priority_queue 就可以了。

但是還有一個問題，如何考慮下面這組數據呢？

1 2 5

可以發現，若貪心處理，則僅會在第 1 天買入一股，並在第 2 天賣出，賺到了 1 元。但是若將第 1 天的股票在第 3 天賣出，則可以獲得高達 4 元的利潤，比原答案不知道高到哪里去了。

---

所以我們嘗試去考慮設計一種反悔策略，使所有的貪心情況都可以得到全局最優解。（即設計反悔自動機的反悔策略）

定義 \(C_{buy}\) 為全局最優解中買入當天的價格，\(C_{sell}\) 為全局最優解中賣出當天的價格，則：

\[C_{sell} - C_{buy} = (C_{sell} -C_i) + (C_i - C_{buy}) \]

\(C_i\) 為任意一天的股票價格

即我們買價格最小的股票去賣價格最大的股票，以期得到最大的利潤。我們先把當前的價格放入小根堆一次（這次是以上文的貪心策略貪心），判斷當前的價格是否比堆頂大，若是比其大，我們就將差值計入全局最優解，再將當前的價格放入小根堆（這次是反悔操作）。相當於我們把當前的股票價格若不是最優解，就沒有用，最后可以得到全局最優解。

上面的等式即被稱為反悔自動機的反悔策略，因為我們並沒有反復更新全局最優解，而是通過差值消去中間項的方法快速得到的全局最優解。

Code:

struct node {
    int value;
    // 重載<號的定義，規定堆為關於價值的小根堆
    bool operator<(const node &b) const {
        if (value > b.value) return true;
        return false;
    }
} a[330000];
priority_queue<node> q;
int n;
ll cnt = 0;

int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i].value;

    for (int i = 1; i <= n; ++i) {
        q.push(a[i]);  //用於貪心買價格最小的股票去買價格最大的股票
        //假如當前的股票價格不是最優解
        if (q.size() && q.top().value < a[i].value) {
            cnt += a[i].value - q.top().value;  //將差值計入全局最優解
            // 將已經統計的最小的股票價格丟出去，並執行反悔策略：將當前的股票價格再放入堆中，即記錄中間變量（等式中間的Vi)
            q.pop(), q.push(a[i]);
        }
    }
    cout << cnt << "\n";
    return 0;
}

雙向鏈表反悔自動機

BZOJ2151 種樹（雙向鏈表反悔自動機）

Description:

有 \(n\) 個位置，每個位置有一個價值。有 \(m\) 個樹苗，將這些樹苗種在這些位置上，相鄰位置不能都種。求可以得到的最大值或無解信息。

Method：

先判斷無解的情況，我們顯然可以發現，若 \(m>\frac{n}2\) ，則是不能在合法的條件下種上 m 棵樹的，故按題意輸出Error!即可。

假如有解的話，我們可以很輕松的推出貪心策略：在合法的情況下選擇最大的價值。

顯然上面的策略是錯誤的，我們選擇了最大價值的點，相鄰的兩個點就不能選，而選擇相鄰兩個點得到的價值可能更大。

考慮如何設計反悔策略。

我們同樣用差值來達到反悔的目的。假設有 \(A ，B ，C ，D\) 四個相鄰的點（如圖）。

\(A\) 點的價值為 \(a\) ，其他點同理。若

\[a + c > b + d \]

則：

\[a + c - b > d \]

假如我們先選了 \(B\) 點，我們就不能選 \(A\) 和 \(C\) 兩點，這顯然是不對的，但我們可以新建一個節點 \(P , P\) 點的價值為 $a+c−b $，再刪去 \(B\) 點。（如圖，紅色的是刪去的點，橙色的新建的點)

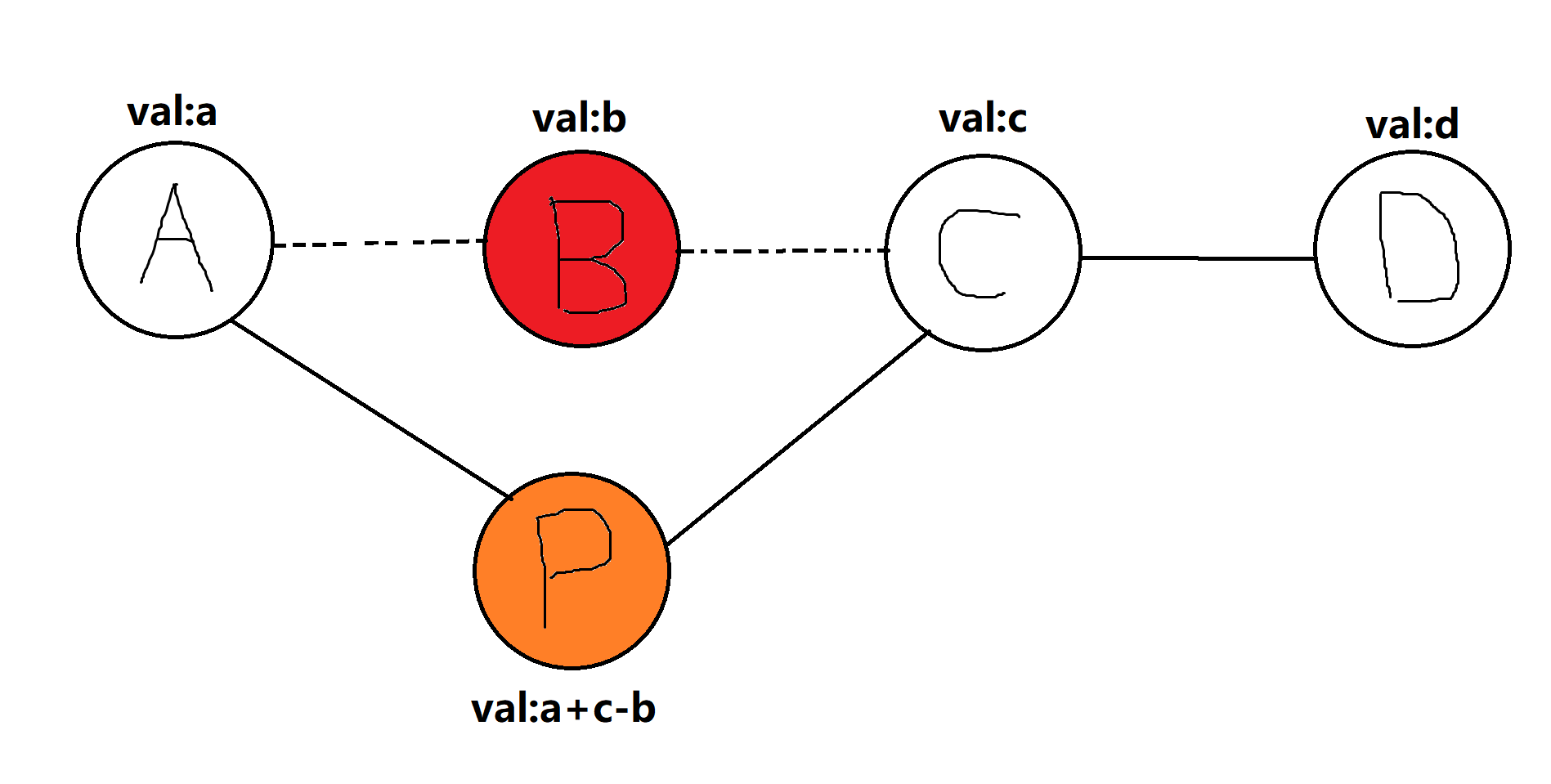
下一次選擇的點是 P 的話，說明我們反悔了（即相當於 B 點沒有選），可以保證最后的貪心最優解是全局最優解。

如何快速插入 P 點和找出是否選擇 P 點呢？我們可以使用雙向鏈表和小根堆，使得最終在 \(O(nlog⁡n)\) 的時間復雜度下快速求出全局最優解.

注意點：

• 一定要記錄這個點選沒有選過，假如已經選過了，就從堆中丟出去；
• 1 與 n 是相鄰的，一定要特判一下；
• 雙向鏈表一定不要寫掛了；
• 一定要先將新建的點的價值存入一開始的價值數組，再丟進堆里；（不然會卡數據）

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 2e6 + 10;
struct node {
    int val, id;
    bool operator<(const node& x) const { return val < x.val; }
} now, x;
ll val[N];              // 價值
ll vis[N], l[N], r[N];  // vis記錄是否刪除,l、r為雙向鏈表的左右點

int t, n, m;
ll ans = 0;
priority_queue<node> q;
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> val[i];
    while (q.size()) q.pop();

    // 初始化堆
    for (ll i = 1; i <= n; ++i) {
        now.id = i, now.val = val[i];
        vis[i] = 0;
        q.push(now);
    }

    // 處理雙向鏈表
    for (int i = 2; i <= n; ++i) l[i] = i - 1;
    for (int i = 1; i <= n; ++i) r[i] = i + 1;

    l[1] = r[n] = 0;

    for (int i = 1; i <= m; ++i) {
        x = q.top(), q.pop();
        while (vis[x.id] == 1) {  //找到一個沒有被刪除的值最大的點
            x = q.top(), q.pop();
        }

        if (x.val < 0) break;
        ans += x.val;
        if (l[x.id] != 0) vis[l[x.id]] = 1;  //刪除左邊的點
        if (r[x.id] != 0) vis[r[x.id]] = 1;  //刪除右邊的點

        if (l[x.id] != 0 && r[x.id] != 0) {
            now.id = x.id;
            now.val = val[x.id] = val[l[x.id]] + val[r[x.id]] - val[x.id];

            r[l[l[x.id]]] = x.id;
            l[x.id] = l[l[x.id]];
            l[r[r[x.id]]] = x.id;
            r[x.id] = r[r[x.id]];
            q.push(now);
        } else if (l[x.id])
            r[l[l[x.id]]] = 0;
        else
            l[r[r[x.id]]] = 0;
    }
    cout << ans << "\n";
    return 0;
}