真的超詳細又好懂的梯度下降優化算法概覽

參考 https://ruder.io/optimizing-gradient-descent/ 。

本文不是簡單地翻譯，而是真的花了一天的時間和心思來寫，這一過程中我也重新復習了一遍，而且對不太容易理解的地方都做了詳細的解釋和說明，如果看了本文還不清楚，那。。。那你就來我公眾號后台私信我交流！！！記得加個關注，最好是打賞支持一下哈哈哈，共勉！

1. 為什么有了Mini-batch SGD還不滿足？

\[\theta = \theta - \eta \cdot \nabla_\theta J( \theta; x^{(i:i+n)}; y^{(i:i+n)}) \tag{1} \]

朴素(Vanilla) mini-batch梯度下降優化算法雖然在大多時候都夠用，但是還有不少問題為解決：

• 我們很難選擇一個合適的學習率。因為太小的話收斂太慢，太大則可能會使得損失函數在局部最低點震盪（fluctuate）甚至是不收斂。
• 學習率不能根據數據集的特點靈活變動。雖然我們有時會使用learning rate scheduler來調整學習率，但是調整的規則需要事先定義好。
• 所有的權重使用的是同樣的學習率。如果我們的數據是sparse的，或者說數據特征之間的頻率 ^[1] 差別很大，我們肯定不希望他們的更新幅度保持一樣。
• 另一個很難解決的問題是極端情況下的非凸損失函數。常說的陷於局部最優點倒是其次，鞍點（saddle point） 才是最難解決的問題，因為鞍點附近的梯度接近於0，此時常規的SGD算法很難逃出鞍點。

因此為了解決這些問題，或者說是挑戰，有很多改進版的優化算法被相繼提出。

下面我會盡可能直觀地對這些改進算法進行介紹。

2. Momentum

在介紹結合Momentum的優化器時，經常能看到如上兩張圖。一般的解釋是Vanilla SGD會在ravine（峽谷）區域震盪的特別厲害，加了momentum之后就會改善很多。其實基於上面的圖我是不太理解這個所謂的震盪是什么意思，以及為什么它就震盪了，所以我畫了下面的圖幫助理解。

Ravine的定義 ^[2] 是：Ravines are areas where the surface curves much more steeply in one dimension than in another.

黑色箭頭表示優化方向和步長，可以看到相比於下半段，上半段的紅色曲線部分變化幅度更加陡峭，因此SGD的更新也是一會朝上一會朝下，這就是所謂的震盪。到了下半段之后，紅色曲線平緩一些了，所以黑色箭頭的方向也都是朝下。

但是從全局的角度來看，上半段的震盪式更新很慢，Momentum的提出就是為了幫助SGD在相關方向上加速，從而抑制震盪（dampen oscillations）。

Momentum計算公式如下：

\[\begin{align} \begin{split} v_t &= \gamma v_{t-1} + \eta \nabla_\theta J( \theta) \\ \theta &= \theta - v_t \end{split} \tag{2} \end{align} \]

可以看到相比於公式（1），Momentum會把之前的更新幅度也考慮進來。我們舉一個具體的例子來幫助理解。

假設第一次更新幅度\(v_0=0.6\)（因為第一次沒有\(v_{t-1}\)，所以就等於梯度值）。也就是說第一次更新方向是正方向，步長是0.6。

第二次的梯度值是 -0.2,如果是朴素SGD，那么就會往回走0.2，但是因為因為了momentum，那么此次的更新幅度就是 +0.34，也就是說還是會繼續往正方向更新。

到了第三次，梯度值為 -0.8， 此時總的更新幅度變成了 -0.494,更新方向發生了改變。

\[\begin{align} \begin{split} v_0&=0.6 \\ v_1&=0.9*0.6+\eta \nabla_\theta J( \theta)\\ &=0.54-0.2=0.34 \\ v_2&=0.9*0.34+\eta \nabla_\theta J( \theta)\\ &=0.9*0.34-0.8=-0.494 ... \end{split} \notag \end{align} \]

3. Nesterov accelerated gradient

我們可以把Momentum優化器簡單理解成一個在山坡上滾動的球，如果山坡一直是朝下的，那么小球的速度會越來越快。但是這樣就會有一個新的問題，如果突然有一段很長的上升的坡，那么小球則會因為慣性沖上去，這顯然是我們不想要的。

Nesterov accelerated gradient (NAG) ^[3] 的解決思路是讓這個小球能夠意識到自己大概處在什么位置，從而能預測在上升坡到來之前先減慢速度。

NAG在Momentum的基礎上做了很小的改動就能實現上面的想法，公式如下：

\[\begin{align} \begin{split} v_t &= \gamma v_{t-1} + \eta \nabla_\theta J( \theta - \gamma v_{t-1} ) \\ \theta &= \theta - v_t \end{split} \tag{3} \end{align} \]

可以看到變化的地方只是把\(\theta\)換成了\(\theta - \gamma v_{t-1}\)，這樣做是什么意思呢？我們結合下圖^[4]來理解。

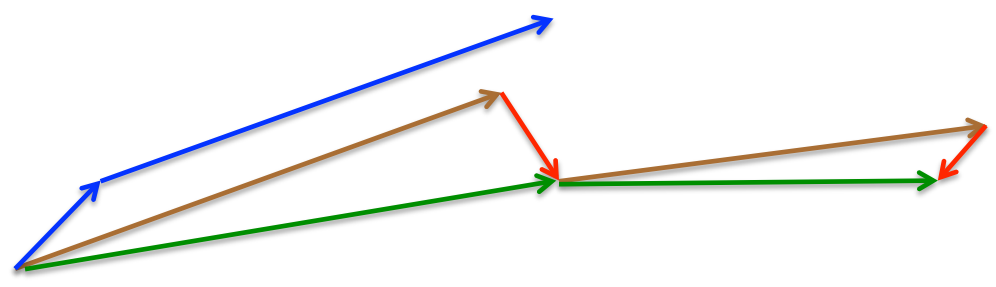
短一點的藍色箭頭表示當前時刻的梯度值，長一點的藍色箭頭表示Momentum計算得到的累積梯度（即\(v_{t-1}\)）。NAG首先是基於上一時刻的梯度對參數進行計算（棕色箭頭,其與長藍色箭頭平行）,之后基於該點計算用於糾正的梯度值（紅色箭頭），最后總的更新方向和幅度就是綠色箭頭。

4. Adagrad

前面提到的Vanilla SGD，SGD-Momentum，NAG都是采用同樣的學習率來更新所有參數。Adagrad則可以對不同的參數使用不同的學習率進行更新：對於那些出現頻率較多出現（frequently occuring）的特征會使用較小的學習率，而對那些較少出現的特征使用較大的學習率。因此，Adagrad十分適合處理sparse data。

下面介紹Adagrad的計算方式，首先給定符號定義：

• \(\theta\)表示所有的參數，\(\theta_i\)表示某一個參數。Adagrad是對每一個參數采用不同的學習率。
• \(g_t\)表示在\(t\)時刻的梯度，而\(g_{t,i}\)則表示\(t\)時刻每一個參數\(\theta_i\)對應的梯度，即\(g_{t,i}=\eta \nabla_\theta J( \theta_{t,i})\)

那么Vanilla SGD的表達形式則是：

\[\theta_{t+1, i} = \theta_{t, i} - \eta \cdot g_{t, i} \tag{4.1} \]

Adagrad對上面公式中的\(\eta\)做了修正：

\[\theta_{t+1, i} = \theta_{t, i} - \dfrac{\eta}{\sqrt{G_{t, ii} + \epsilon}} \cdot g_{t, i} \tag{4.2} \]

\(G_{t} \in \mathbb{R}^{d \times d}\)是一個對角矩陣，對角線上的元素\(G_{t, ii}\)是從初始時刻到t時刻為止，所有關於\(\theta_i\)的梯度的平方和，即\(G_{t, ii}=\sum_{k=0}^{t-1} \sqrt{G_{k, ii}}\)。 \(\epsilon\) 是噪聲值，通常大小為\(1e-8\)，主要是為了避免分母為0。有實驗表明，如果不計算平方根，Adagrad的效果會很差。

上面的式子是針對每個元素的計算方式，下面我們使用矩陣計算（ \(\odot\) 表示矩陣乘法）的表達方式推廣到所有元素，即

\[\theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{G_{t} + \epsilon}} \odot g_{t} \tag{4.3} \]

使用Adagrad的主要優點是我們無需在手動調整學習率，一般來說只需要把學習率設置為0.01就好了，不再需要調用lr scheduler。

Adagrad的缺點也很明顯，由於分母是從初始時刻到t時刻所有梯度的平方和，也就是說分母會隨着時間不斷變大，那么一定時間后，分母會特別大，以至於學習率接近於0，此時更新幅度也基本上停止了，那么啥東西也沒法學了。所以下面的Adadelta算法就是為了解決這個問題。

5. Adadelta

Adagrad是把前面所有時刻的梯度做了平方和的計算，那么一個很直觀且naive的想法是我們只選取前\(W\)個時刻的梯度做平方和計算即可。

Adadelta的確采用了類似的做法，它借鑒了Momentum的思路，即當前時刻的滑動平均\(E[g^2]_t\)依賴於上一時刻的滑動平均\(E[g^2]_{t-1}\)和當前時刻的梯度值\(g_t\)，即：

\[E[g^2]_t = \gamma E[g^2]_{t-1} + (1 - \gamma) g^2_t \tag{5.1} \]

\(\gamma\)類似於Momentum term,通常設置在0.9左右。當\(\gamma=0.5\)時，上式就變成了梯度平方和。

那么Adadelta的參數更新公式為：

\[\theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} \odot g_{t} \tag{5.2} \]

通常\(\sqrt{E[g^2]_t + \epsilon}\)也會簡寫成\(RMS[g]_t\), (RMS是root mean squared的縮寫)

所以

\[\begin{align} \theta_{t+1} &= \theta_{t} + \Delta \theta_t \notag\\ &=\theta_t - \dfrac{\eta}{RMS[g]_t} \odot g_t \tag{5.3} \end{align} \]

此時Adadelta還是依賴全局學習率的，所以作者還進一步定義了另一個指數衰減平均，這次不是梯度平方，而是參數的平方的更新：

\[E[\Delta \theta^2]_t = \gamma E[\Delta \theta^2]_{t-1} + (1 - \gamma) \Delta \theta^2_t \tag{5.4} \]

類似地有

\[RMS[\Delta \theta]_{t} = \sqrt{E[\Delta \theta^2]_t + \epsilon} \tag{5.5} \]

最后通過一通騷操作（一階近似Hessian方法 ^[5] ）后，式(5.3)近似為如下：

\[\begin{align} \begin{split} \Delta \theta_t &= - \dfrac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}} g_{t} \\ \theta_{t+1} &= \theta_t + \Delta \theta_t \end{split} \tag{5.6} \end{align} \]

至此，Adadelta介紹結束了，我們通過上式可以看到，學習率\(\eta\)消失了，換句話說有了Adadelta之后，我們甚至可以不用設置默認的學習率。（機器之心震驚體可以用起來了！！！）

6. RMSprop

RMSprop是由Geoff Hinton大佬在其Coursera課堂的課程中提出的，換句話說它還是一個尚未發表的自適應學習率的算法，

RMSprop和Adadelta幾乎是在在相同的時間里被獨立的提出，都是為了解決Adagrad的極速遞減的學習率問題。RMSprop可以算作Adadelta的一個特例，即式子(5.3)。也就是說，RMSprop還是依賴於全局學習率，非常適合處理非平穩目標（對RNN效果會比較好）。

常用的參數設置如下：

\[\begin{align} \begin{split} E[g^2]_t &= 0.9 E[g^2]_{t-1} + 0.1 g^2_t \\ \theta_{t+1} &= \theta_{t} - \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t} \end{split} \tag{6} \end{align} \]

Hinton建議將\(\gamma\)設置為0.9，對於學習率\(\eta\)，推薦設置為0.001。

7. Adam

終於到Adam神器了，其全稱是Adaptive Moment Estimation ^[6]。 Adam也是會給每個參數計算動態的學習率。

除了像Adadelta和RMSprop那樣需要計算過去平方梯度\(v_t\)的指數衰減平均值外，Adam還需要類似於Momentum的做法來保存過去梯度\(m_t\)的指數衰減平均值,簡單理解就是Adam = RMSprop + Momentum。

\[\begin{align} \begin{split} m_t &= \beta_1 m_{t-1} + (1 - \beta_1) g_t \\ v_t &= \beta_2 v_{t-1} + (1 - \beta_2) g_t^2 \end{split} \tag{7.1} \end{align} \]

不同論文的符號不一樣，所以看起來會有點混亂，這里Adam的\(v_t\)就是前面Adadelta中的\(E[g^2]_t\)，\(m_t\)就是Momentum公式中的\(v_t\)。\(\beta_1,\beta_2\)則類似前面的\(\gamma\)

一般而言，一個向量通常是初始化為0向量，但是在這里，如果我們也把\(v_t,m_t\)初始化為\(\vec{0}\)，那么有如如下推導 ^[7]（下面的推導很多教程根本都不提!!!），

\[\begin{array}{c} m_{0}=0 \\ m_{1}=\beta_{1} m_{0}+\left(1-\beta_{1}\right) g_{1}=\left(1-\beta_{1}\right) g_{1} \\ m_{2}=\beta_{1} m_{1}+\left(1-\beta_{1}\right) g_{2}=\beta_{1}\left(1-\beta_{1}\right) g_{1}+\left(1-\beta_{1}\right) g_{2} = (1-\beta_1)(\beta_1g_1+g_2)\\ m_{3}=\beta_{1} m_{2}+\left(1-\beta_{1}\right) g_{3}=\beta_{1}^{2}\left(1-\beta_{1}\right) g_{1}+\beta_{1}\left(1-\beta_{1}\right) g_{2}+\left(1-\beta_{1}\right) g_{3} = (1-\beta_1)(\beta_1^2g_1+\beta_1g_2+g_3) \end{array} \]

所以我們得到t時刻

\[m_t =(1-\beta_1) \sum_{i=1}^t \beta_1^{t-i} g_i \tag{7.2} \]

進一步可以得到

\[\begin{array}{c} E\left[m_{t}\right]=E\left[\left(1-\beta_{1}\right) \sum_{i=1}^{t} \beta_{1}^{-i} g_{i}\right] \\ =E\left[g_{i}\right]\left(1-\beta_{1}\right) \sum_{i=1}^{t} \beta_{1}^{t-i}+\zeta \\ =E\left[g_{i}\right]\left(1-\beta_{1}^{t}\right)+\zeta \tag{7.3} \end{array} \]

第一行到第二行是一個近似，所以后面需要加一個誤差值\(\zeta\)。最后我們可以看到\(E[m_t]\)和\(E[g_t]\)之間有一個偏差\(1-\beta_1^t\),所以為了修正偏差（\(v_t\)修正同理），有

\[\begin{align} \begin{split} \hat{m}_t &= \dfrac{m_t}{1 - \beta^t_1} \\ \hat{v}_t &= \dfrac{v_t}{1 - \beta^t_2} \end{split} \tag{7.4} \end{align} \]

通常\(\beta_1=0.9, \beta_2=0.999,\eta=10^{-8}\)最后將\(\hat{m}_{t}\)和\(\hat{v}_{t}\)代入公式(6)后，Adam梯度更新算法公式為

\[w_{t}=w_{t-1}-\eta \frac{\hat{m}_{t}}{\sqrt{\hat{v}_{t}}+\epsilon} \tag{7.5} \]

Adam的python實現代碼如下

for t in range(num_iterations):
    g = compute_gradient(x, y)
    m = beta_1 * m + (1 - beta_1) * g
    v = beta_2 * v + (1 - beta_2) * np.power(g, 2)
    m_hat = m / (1 - np.power(beta_1, t))
    v_hat = v / (1 - np.power(beta_2, t))
    w = w - step_size * m_hat / (np.sqrt(v_hat) + epsilon)

8. AdaMax

AdaMax是在Adam的基礎上做了一丟丟的改進。由公式(7.1)可以知道Adam在計算\(v_t\)時采用的\(\ell_2\) norm,即

\[v_t = \beta_2 v_{t-1} + (1 - \beta_2) |g_t|^2 \]

那么很自然地我們會想是否可以推廣到任意的norm呢？所以AdaMax的做法是

\[v_t = \beta_2^p v_{t-1} + (1 - \beta_2^p) |g_t|^p \tag{8.1} \]

注意，上式中\(\beta_2\)也引入了\(\ell_p\) norm。當\(p\)值較大時，norm計算起來不穩定，所以這也是為什么1-norm和2-norm是最常用的。但是AdaMax作者發現\(\ell_\infty\)表現更好，所以這也是為什么叫做AdaMax了。

為了避免和Adam混淆，我們使用\(u_t\)來表示無窮范數約束的\(v_t\),即

\[\begin{align} \begin{split} u_t &= \beta_2^\infty v_{t-1} + (1 - \beta_2^\infty) |g_t|^\infty\\ & = \max(\beta_2 \cdot v_{t-1}, |g_t|) \end{split} \tag{8.2} \end{align} \]

將\(u_t\)代入公式(7.5)可得

\[\theta_{t+1} = \theta_{t} - \dfrac{\eta}{u_t} \hat{m}_t \tag{8.3} \]

推薦的參數設置如下：

\(\eta=0.002,\beta_1=0.9,\beta_2=0.999\)

9. Nadam

Adam = RMSprop + Momentum

Nadam ^[8] = NAG + Adam

9.1 NAG→Nadam

我們先介紹如何引入NAG算法。不過在此之前我們回顧一下Momentum更新算法的公式：

\[\begin{align} \begin{split} g_t &= \nabla_{\theta_t}J(\theta_t)\\ m_t &= \gamma m_{t-1} + \eta g_t\\ \theta_{t+1} &= \theta_t - m_t \\ &= \theta_t - (\gamma m_{t-1} + \eta g_t) \end{split} \tag{9.1} \end{align} \]

所以momentum的更新方向是 前一時刻的momentum 加上 當前時刻的梯度 這兩個矢量的方向。

之后的NAG算法對更新方向做了修正，解決momentum剎不住車的問題。公式如下，可以看到上一時刻的momentum \(m_{t-1}\)被使用了兩次，一次是用來更新\(g_t\)，一次是用來更新\(\theta_{t+1}\)。

\[\begin{align} \begin{split} g_t &= \nabla_{\theta_t}J(\theta_t - \gamma m_{t-1})\\ m_t &= \gamma m_{t-1} + \eta g_t\\ \theta_{t+1} &= \theta_t - m_t \\ &= \theta_t - (\gamma m_{t-1} + \eta g_t) \end{split} \tag{9.2} \end{align} \]

NAG的思想主要是在計算梯度\(g_t\)時使用了未來位置：\(\theta_t - \gamma m_{t-1}\)。換句話說，只要計算梯度時考慮了未來的因素，那應該也能達到NAG的效果 ^[9]。 因此在Nadam中，\(g_t\)的計算仍然使用原來的計算方式，即\(g_t = \nabla_{\theta_t}J(\theta_t)\)，但是在迭代更新\(\theta_{t+1}\)時則使用未來時刻的momentum \(m_{t+1}\)也就行了，所以引入NAG后的計算公式為：

\[\begin{align} \begin{split} g_t &= \nabla_{\theta_t}J(\theta_t)\\ m_t &= \gamma m_{t-1} + \eta g_t\\ m_{t+1} &\approx \gamma m_{t} + \eta g_t\\ \theta_{t+1} &= \theta_t -m_{t+1}\\ &=\theta_t - (\gamma m_t + \eta g_t) \end{split} \tag{9.3} \end{align} \]

(9.3)的第3行你可能會好奇為什么未來時刻的momentum \(m_{t+1}\approx \gamma m_{t} + \eta g_t\)，推理如下：
- 因為 \(m_t = \gamma m_{t-1} + \eta g_t\)，那么\(m_{t+1} = \gamma m_{t} + \eta g_{t+1}\)
- 假設連續兩次的梯度變化不大，那么則有\(g_{t+1}\approx g_t\)
- 所以\(m_{t+1}\approx \gamma m_{t} + \eta g_t\)

所以(9.1)變成(9.3)並不是簡單地理解成把\(m_{t-1}\)替換成\(m_t\)。不過上面的分析也可以知道Nadam使用的場景是梯度不會發生劇烈變化，否則上邊的式子就不成立了。

9.2 Adam→Nadam

由9.1節可以知道，引入NAG的方法簡單理解就是在更新\(\theta_{t+1}\)的時候，把\(m_{t-1}\)替換成\(m_t\)（注意，只是為了方便后面那說明才這么寫，其實並不是簡單替換，9.1節最后已經說明過了），那么下面就是把Adam引入進來，在介紹之前還是回顧一下Adam的計算規則：

\[\begin{align} \begin{split} m_t &= \beta_1 m_{t-1} + (1 - \beta_1) g_t\\ \hat{m}_t & = \frac{m_t}{1 - \beta^t_1}\\ \theta_{t+1} &= \theta_{t} - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t \\ &= \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t} + \epsilon} (\dfrac{\beta_1 m_{t-1}}{1 - \beta^t_1} + \dfrac{(1 - \beta_1) g_t}{1 - \beta^t_1}) \end{split} \tag{9.4} \end{align} \]

簡單理解，引入NAG時把\(m_{t-1}\)替換成了\(m_t\)，同樣地我們也可以對(9.4)最后一行做同樣操作后則可以得到Nadam最終的計算規則了：

\[\begin{align} \begin{split} \theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t} + \epsilon} (\dfrac{\beta_1 m_{t}}{1 - \beta^t_1} + \dfrac{(1 - \beta_1) g_t}{1 - \beta^t_1})\\ = \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t} + \epsilon} (\beta_1 \hat{m}_t + \dfrac{(1 - \beta_1) g_t}{1 - \beta^t_1}) \end{split} \tag{9.5} \end{align} \]

碼字不易，給個贊或打個賞吧。有問題歡迎公眾號后台討論或者評論區留言，謝謝！

微信公眾號：AutoML機器學習
MARSGGBO♥原創
如有意合作或學術討論歡迎私戳聯系~
郵箱:[e-mail]
2021年1月30日09:39:34

---

1. https://www.zhihu.com/question/20099543 ↩︎

2. Sutton, R. S. (1986). Two problems with backpropagation and other steepest-descent learning procedures for networks. Proc. 8th Annual Conf. Cognitive Science Society. ↩︎

3. Nesterov, Y. (1983). A method for unconstrained convex minimization problem with the rate of convergence o(1/k2). Doklady ANSSSR (translated as Soviet.Math.Docl.), vol. 269, pp. 543– 547. ↩︎

4. Source: G. Hinton's lecture ↩︎

5. 自適應學習率調整：AdaDelta: https://www.cnblogs.com/neopenx/p/4768388.html ↩︎

6. Kingma, D. P., & Ba, J. L. (2015). Adam: a Method for Stochastic Optimization. International Conference on Learning Representations, 1–13. ↩︎

7. https://towardsdatascience.com/adam-latest-trends-in-deep-learning-optimization-6be9a291375c ↩︎

8. Dozat, T. (2016). Incorporating Nesterov Momentum into Adam. ICLR Workshop, (1), 2013–2016. ↩︎

9. 從 SGD 到 Adam —— 深度學習優化算法概覽(一)
   https://zhuanlan.zhihu.com/p/32626442 ↩︎