對隨機變量X的概率密度函數f(x)做積分運算,我們就可以通過
\[E(g(X))=\int_{-\infty}^{+\infty}{g(x)f(x)}dx \]
這樣的積分形式來表示指定函數g在參數X時函數值的期望值。
基於蒙特卡洛方法的數值積分正好是這種方法的逆推。如果我們需要計算某個定積分的值,只要將其變換為某一隨機變量的期望的形式,再借用蒙特卡洛方法即可。
例如,如果需要計算
\[c=\int_a^b{h(x)}dx \]
我們應令X遵從[a,b]上的均勻分布,且g(x)=(b-a)h(x),對g(x)施加蒙特卡洛方法,就可以得到E(g(X))=c。之后,只要將生成的偽隨機數序列x1,x2....xn來模擬[a,b]上的均勻分布,就可以通過計算(b-a)(h(x1)+....h(xn))/n來得到c的估計值。
下面通過例子來用蒙特卡洛方法來計算
\[\int_0^2{x^2}dx \]
故
\[g(x)=2x^2 \]
已知c的理論解是8/3
python代碼:
import numpy as np
n=100000 #隨機數的數量
x=2*np.random.rand(n) #在[0,2]上的n個隨機數
c=np.sum(2*x**2)/n
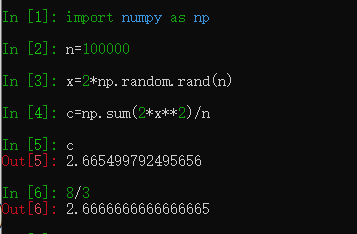
可見,用蒙特卡洛法求得的積分值與理論解非常接近。
