L1,L2正則化與損失

L1和L2是指范數，分別為1范數和2范數。

損失

L1損失

MAE(Mean absolute error)損失就是L1損失，目標值\(\boldsymbol{y}\)，目標函數\(f(\cdot)\)，輸入值\(\boldsymbol{x}\)，則：

\[\begin{aligned} L_1 &= \|f(\boldsymbol{x}) - \boldsymbol{y}\|_1\\\\ &= \sum\limits_i {|f({x_i}) - {y_i}|} \end{aligned} \]

L2損失

MAE(Mean square error)損失就是L2損失，目標值\(\boldsymbol{y}\)，目標函數\(f(\cdot)\)，輸入值\(\boldsymbol{x}\)，則：

\[\begin{aligned} L_2 &= \|f(\boldsymbol{x}) - \boldsymbol{y}\|_2\\\\ &= {\sum\limits_i {(f({x_i}) - {y_i}})^2} \end{aligned} \]

test

正則化

正則化與損失不同，借用某知乎網友回答，就是Regularize。正則項對應就是個調節器Regularizer，使模型不過擬合罷了，中文翻譯真的坑。至於為何使用L1或者L2損失，不過是希望使目標函數中的權重更稀疏罷了，這樣參與計算的多項式的項更少。也就是希望權重向量\(\boldsymbol{w}\)中0元素更多（0范數）。

\[\begin{aligned} f(\boldsymbol{x}) = w_1x_1+w_2x_2+...+w_nx_n \end{aligned} \]

\(L1\)或者\(L2\)正則只是使\(\boldsymbol{w}\)的某種幾何度量更小，不能直接達到稀疏的期望。使得\(\boldsymbol{w}\)的范數更小，也算是某種平滑吧，這樣就不會因為\(\|\boldsymbol{w}\|\)過大而過度偏向某個維度的\(x_i\)(即過擬合)，\(w_i\)值的增加會一定程度上(\(\lambda\))造成Loss的增加，從而避免過擬合。

至於L1比L2正則“尖銳”之說可以認為在最優點附近，L1函數導數比L2導數大，更容易逼近0值，當然也容易不優而已，具體哪種正則好其實看任務本身。

L1正則化

正則項加入損失函數中實現正則化，以向L1損失加入L1正則為例。輸入值\(\boldsymbol{x}\)，目標值\(\boldsymbol{y}\)，目標函數$f(\boldsymbol{x}) =\boldsymbol{w}\boldsymbol{x} $。則損失函數：

\[\begin{aligned} L_{r1} &= \|\boldsymbol{wx}-\boldsymbol{y}\|_1+\|\boldsymbol{w}\|_1\\\\ &= \sum\limits_i {| {w_ix_i} - y_i|+ \lambda |w_i|} \end{aligned} \]

L2正則化

以L2損失加入L2正則為例。輸入值\(\boldsymbol{x}\)，目標值\(\boldsymbol{y}\)，目標函數$f(\boldsymbol{x}) =\boldsymbol{w}\boldsymbol{x} $。則損失函數：

\[\begin{aligned} L_{r2} &= \|\boldsymbol{w}\boldsymbol{x}-\boldsymbol{y}\|_2+ \|\boldsymbol{w}\|_2\\\\ &= \sum\limits_i {( {w_ix_i} - y_i)^2+\lambda (w_i)^2} \end{aligned} \]

解釋

目前流行3種解釋法說明L1比L2正則化更容易獲得稀疏解，也就是更容易獲得欠擬合（不過擬合）解。

• 導數解釋
  \(w_i\)在0值附件時，L1范數的導數在左右震動，幅度為\(2\lambda\)，該震盪產生導數為0的次優解，即\(w_i=0\)變成次優解，即模型多了許多\(w_i=0\)的解。

\[\begin{aligned} \frac{\partial{Loss}}{\partial{w_i}}|_0=d_0+\lambda或者 d_0-\lambda \end{aligned} \]

根據中值定理，該導數值必過0點，即次優解點，而這個點為\(w_i=0\)的點。

• 圖形解釋
  以二維空間為例，即n=2，\(w_1\)和\(w_2\)構成橫縱坐標。
  
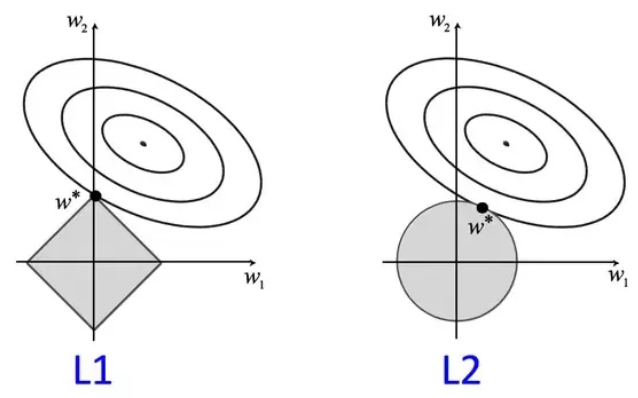
  加入正則項的損失的理論解可以看作，存在\(\boldsymbol{w}\)，使無正則損失loss=\(-\lambda *\)正則項。從圖上看，無正則損失分布在二維空間任意移動時，左邊圖更容易取到\(w_i=0\)的解。
• 先驗分布解釋
  L1相當於加了拉普拉斯分布，L2相當於加了高斯分布。從概率密度上說，在接近\(w_i=0\)的位置，拉普拉斯分布在\(w_i=0\)附近更尖銳，占據的概率分布更多。

code

class Regularization(torch.nn.Module):
    def __init__(self,model,weight_decay,p=2):
        '''
        :param model 模型
        :param weight_decay:正則化參數
        :param p: 范數計算中的冪指數值，默認求2范數,
                  當p=0為L2正則化,p=1為L1正則化
        '''
        super(Regularization, self).__init__()
        if weight_decay <= 0:
            print("param weight_decay can not <=0")
            exit(0)
        self.model=model
        self.weight_decay=weight_decay
        self.p=p
        self.weight_list=self.get_weight(model)
        self.weight_info(self.weight_list)
 
    def to(self,device):
        '''
        指定運行模式
        :param device: cude or cpu
        :return:
        '''
        self.device=device
        super().to(device)
        return self
 
    def forward(self, model):
        self.weight_list=self.get_weight(model)#獲得最新的權重
        reg_loss = self.regularization_loss(self.weight_list, self.weight_decay, p=self.p)
        return reg_loss
 
    def get_weight(self,model):
        '''
        獲得模型的權重列表
        :param model:
        :return:
        '''
        weight_list = []
        for name, param in model.named_parameters():
            if 'weight' in name:
                weight = (name, param)
                weight_list.append(weight)
        return weight_list
 
    def regularization_loss(self,weight_list, weight_decay, p=2):
        '''
        計算張量范數
        :param weight_list:
        :param p: 范數計算中的冪指數值，默認求2范數
        :param weight_decay:
        :return:
        '''
        # weight_decay=Variable(torch.FloatTensor([weight_decay]).to(self.device),requires_grad=True)
        # reg_loss=Variable(torch.FloatTensor([0.]).to(self.device),requires_grad=True)
        # weight_decay=torch.FloatTensor([weight_decay]).to(self.device)
        # reg_loss=torch.FloatTensor([0.]).to(self.device)
        reg_loss=0
        for name, w in weight_list:
            l2_reg = torch.norm(w, p=p)
            reg_loss = reg_loss + l2_reg
 
        reg_loss=weight_decay*reg_loss
        return reg_loss
 
    def weight_info(self,weight_list):
        '''
        打印權重列表信息
        :param weight_list:
        :return:
        '''
        print("---------------regularization weight---------------")
        for name ,w in weight_list:
            print(name)
        print("---------------------------------------------------")

如果有用請給我一個👍，轉載注明：https://allentdan.github.io/