定義
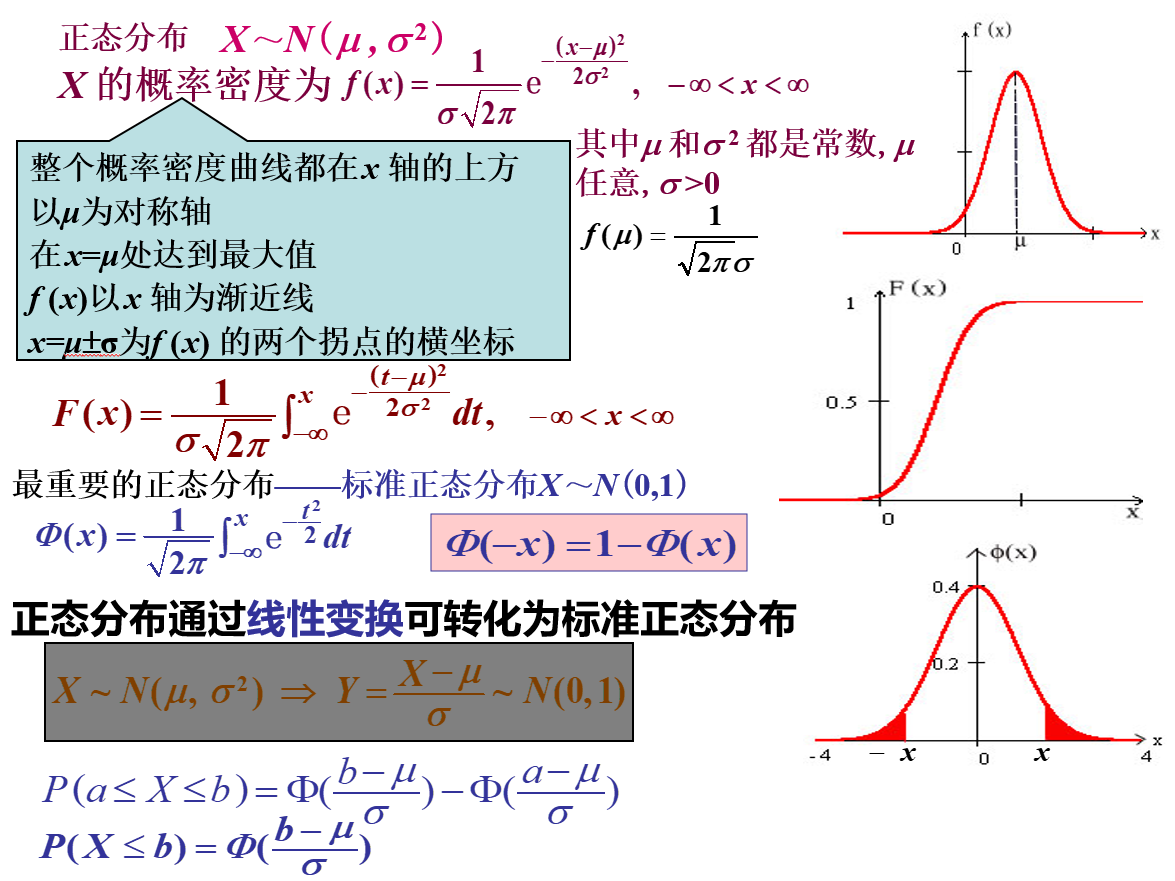
正態分布的期望和方差
期望
\[EX = \mu \]
證明
設隨機變量 \(X \sim N(\mu, \sigma^2)\), 求 \(EX\).
解
\[EX = \int_{-\infty}^{+\infty}xf(x)dx = \displaystyle\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{+\infty}(\sigma t + \mu)e^{-\frac{t^2}{2} }dt \]
\[= \displaystyle\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}\sigma t e^{-\frac{t^2}{2}}dt + \displaystyle\frac{\mu}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}e^{-\frac{t^2}{2}}dt = \mu, \]
即 \(EX = \mu\).
方差
\[DX = \sigma^2 \]
證明
設隨機變量 \(X \sim N(\mu, \sigma^2)\), 求 \(DX\).
解
\[DX = \int_{-\infty}^{+\infty}(x - \mu^2) \times \frac{1}{\sqrt{2\pi}\sigma}exp\left [ -\frac{1}{2}\left ( \frac{x - \mu}{\sigma} \right )^2 \right ]dx = \displaystyle\frac{\sigma ^2}{\sqrt{2\pi}}\int_{-\infty}^{+\infty} t^2 e^{-\frac{t^2}{2}}dt = \displaystyle\frac{1}{\sqrt{2\pi}}\sigma^2\sqrt{2 \pi} = \sigma^2. \]
重要的性質
一般地, 若 \(X_1,...,X_n\) 相互獨立, 且 \(X_i \sim N(\mu, \sigma^2)\), 則
\[\sum_{i = 1}^{n}a_iX_i \sim N(\sum_{i = 1}^{n}a_i\mu_i, \sum_{i = 1}^{n}a_1^2\sigma_i^2). \]
