視覺和IMU的對齊
1. 求陀螺儀的零偏\(b_g\)
視覺計算出了幀間的旋轉,IMU也計算出了幀間的旋轉,這兩者之間並不太一致,那么誰是對的呢?這里采用視覺計算出的值,認為IMU由於零偏的不准確導致計算的旋轉不准確。通過調整零偏,使得目前所有幀的幀間旋轉都盡量的靠近視覺計算的值。同時,這里還假設了零偏沒有錯的太離譜,所以IMU計算的幀間的旋轉(也就是預積分的\(\gamma\))可以用它對零偏的一階泰勒展開來表示。這樣就可以構成一個超定方程組。求解這個方程組,就能夠得到零偏增量的估計,加到原來的零偏上就獲得了新的零偏。
滑窗中各幀已經有了一個up-to-scale的位姿。也有了以初始估計零偏求的的預積分的值。陀螺儀零偏估計,就是要估計出一個陀螺儀零偏,使得滑窗中各幀間由陀螺儀求得的\(\delta q\)與視覺求得的\(\delta q\)的誤差最小。這是一個典型的最小二乘問題。
$$arg\min_{b_g}\sum_{k\in B}\Vert {q{c_0}_{b_{k+1}}}{-1} \otimes q^{c_0}{b_k} \otimes q^{b_k}{b_{k+1}} \Vert^2$$
另外有預積分的一階泰勒近似:
$$q^{b_k}_{b_{k+1}} \approx \hat{q}^{b_k}_{b_{k+1}} \otimes \left [\begin{smallmatrix}1 \\ {1 \over 2} J^q_{b_g} \delta b_g\end{smallmatrix}\right]$$
我們把視覺的測量值當做真值\(q^{b_k}_{b_{k+1}}\),把IMU預積分\(\gamma\)值作為\(\hat{q}^{b_k}_{b_{k+1}}\),這樣就有:
利用它們的虛部相等就可以構建形如\(Ax = b\)的方程。帶求解量是\(\delta b_g\)。
Eigen::Quaterniond q_ij(frame_i->second.R.transpose() * frame_j->second.R);
tmp_A = frame_j->second.pre_integration->jacobian.template block<3, 3>(O_R, O_BG);
tmp_b = 2 * (frame_j->second.pre_integration->delta_q.inverse() * q_ij).vec();
A += tmp_A.transpose() * tmp_A;
b += tmp_A.transpose() * tmp_b;
delta_bg = A.ldlt().solve(b);
具體代碼見: initial_aligment.cpp 函數 solveGyroscopeBias()。
2.線性對齊求出各幀的速度 \(v_k\),重力加速 \(g\)以及尺度 \(s\)
線性對齊就是用IMU預積分\(\alpha, \beta\)值來進行對齊。我們有
可以看到它們其實是兩個時刻距離及速度增量再加上重力加速度的影響。距離跟速度又是相關的。同時,兩幀間的距離又可以通過視覺測量得到。這樣它們就有了對齊的基礎。
我們把上面的世界坐標系替換成\(c_0\)坐標系,並把\(p^w_{b_i}, p^w_{b_j}\)用視覺測量量來代替。由於視覺測量是up-to-scale的,因此要帶上尺度因子。這樣就有:
上式中的$ \bar{p}^{c_0}{b_k}, \bar{p}^{c_0}{b_{k+1}}\(實際上還不是視覺測量, 視覺測量的是camera的距離\)\bar{p}^{c_0}{c_k}, \bar{p}{c_0}_{c_{k+1}}$,它們與$\bar{p}{c_0}{b_k}, \bar{p}{c_0}_{b_{k+1}}$之間可以通過相機與IMU的外參轉換:$\bar{p}{c_0}{b_k} = \bar{P}^{c_0}{c_k} - R{c_0}_{b_k}Pb_c, \quad \bar{p}^{c_0}{b{k+1}} = \bar{P}^{c_0}{c{k+1}} - R{c_0}_{b_{k+1}}Pb_c\(,其中\)P^b_c$表示的是在body坐標系下camera到IMU的距離。代入上式中整理可以得到:
將待估計變量放到方程右邊,寫成矩陣相乘的模式有:
其中:
是待估計的量。
\(n^{b_k}_{b_{k+1}}\)是噪聲項。
這樣就可以構建最小二乘問題。
這里的\(\sum\)的處理需要注意一下。因為在\(k\)時刻的狀態包括\([v^{b_k}_k, v^{b_{k+1}}_{k+1}, g^{c_0}, s]\), 每個時刻跟它的下一個時刻既有相交又有錯位,它們在最終的大矩陣中的位置需要考慮清楚。假如窗口中有10個幀,其實我們可以把每個時刻的狀態都是34維的,而不是10維的,多出的部分用零補足。比如\(0\)時刻\(\mathcal{X}^0_I = [v^{b_0}_0, v^{b_1}_1, 0, \cdots , 0, g^{c_0}, s]\),相應的\(H^{b_0}_{b_1}\)就可以寫成\([A^{0}_{6\times 6}, 0, 0, \cdots, 0, A^{0}_{4\times4}]\)。那么\(H^TH\)就是如下形式:
這樣在大矩陣中的位置就很清楚了。每次時刻遞推,\(A_{6\times 6}\)往右下移動\(3\),\(A_{6\times 4}\)往下移動\(3\), \(A_{4\times 6}\)往右移動\(3\)。
MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;
A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
b.segment<6>(i * 3) += r_b.head<6>();
A.bottomRightCorner<4, 4>() += r_A.bottomRightCorner<4, 4>();
b.tail<4>() += r_b.tail<4>();
A.block<6, 4>(i * 3, n_state - 4) += r_A.topRightCorner<6, 4>();
A.block<4, 6>(n_state - 4, i * 3) += r_A.bottomLeftCorner<4, 6>();
具體代碼見: initial_aligment.cpp 函數 LinearAlignment()。
3.重力向量的進一步優化
上面的到的重力向量無法保證它的模是9.8。因為在上一步中重力向量是一個無約束的3個自由度向量,而實際上重力向量\(g\)只有兩個自由度,它的模是確定的。但是如果將\(g\)的約束加到上面的求解過程中,上面的線性優化問題就變成了非線性優化,增加了復雜度。因此,可以在上一步求出的結果上再次進行優化修正。
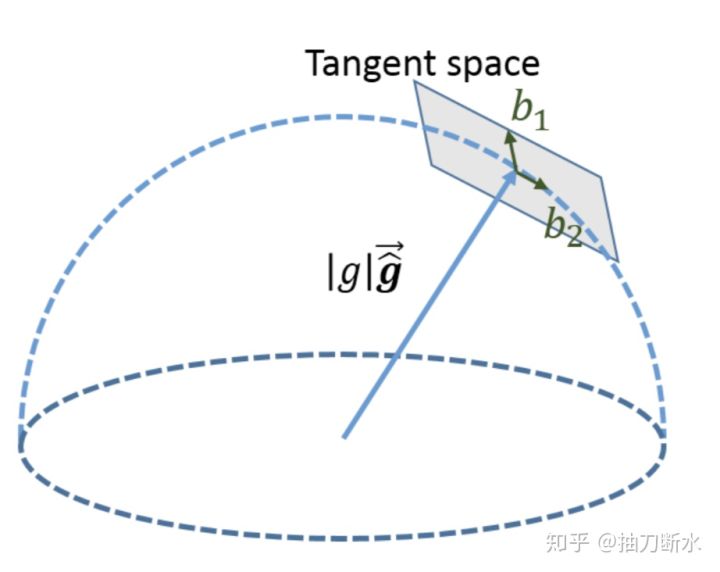
將重力向量參數化為
其中\(b_1, b_2\)是目前估計出的\(g\)切平面的上的一組單位正交基。
將這個重新參數化之后的\(g^{c_0}\)代入到上一步求解的方程中,可以求的對應的\(w_1, w_2\),反復迭代幾次,最終會得到一個收斂的\(g^{c_0}\)。
4.從\(c_0\)坐標系到世界坐標系的旋轉
目前已經知道了\(g^{c_0}\),只要找到一個矩陣把\(g^{c_0}\)旋轉到\(z\)軸, 那么這個矩陣就能夠把\(c_0\)系就與世界坐標系在\(z\)方向上對齊了。不過需要注意的是, IMU的測量量在靜止的時候,除了零偏外,測得的是重力加速度的反向向量。根據前面\(\alpha^{b_k}_{b_{k+1}}, \beta^{b_k}_{b_{k+1}}\)的計算公式,這里的\(g^{c_0}\)其實是加速度的反向。因此這里是把坐標系的\(z\)軸與重力方向的反向對齊,也就是垂直向上。
Eigen::Matrix3d Utility::g2R(const Eigen::Vector3d &g)
{
Eigen::Matrix3d R0;
Eigen::Vector3d ng1 = g.normalized();
Eigen::Vector3d ng2{0, 0, 1.0};
//R0將ng1旋轉到[0,0,1],也就相當於旋轉坐標系把z軸旋轉到了ng1
R0 = Eigen::Quaterniond::FromTwoVectors(ng1, ng2).toRotationMatrix();
double yaw = Utility::R2ypr(R0).x();
//旋轉的過程中可能改變了yaw角,再把yaw旋轉回原來的位置。
//這個是沿z軸的旋轉,因此不改變g沿z軸的方向。只是坐標系的x,y軸改變了。
R0 = Utility::ypr2R(Eigen::Vector3d{-yaw, 0, 0}) * R0;
// R0 = Utility::ypr2R(Eigen::Vector3d{-90, 0, 0}) * R0;
return R0;
}
上面這一步之后,經過\(R_0\)修正,參考坐標系\(z\)軸向下,\(x\)軸是\(c_0\)的前方。不過需要注意的是前面視覺在計算位姿的流程中我們找到與窗口中第一個與滑窗中最后一幀有足夠視差的幀建立參考系,這里的\(c_0\)實際上不一定是第0幀,它在某些情況下可能是第\(x\)幀\(c_x\)。因此,我們要使參考坐標系的\(x\)軸朝向真正的第\(0\)幀的水平正前方。
// R0將參考坐標系旋轉到z軸垂直向上。
Matrix3d R0 = Utility::g2R(g);
// R0將參考系的y軸旋轉到第0幀的IMU正前方,這個時候x軸也確定了向右。
double yaw = Utility::R2ypr(R0 * Rs[0]).x();
R0 = Utility::ypr2R(Eigen::Vector3d{-yaw, 0, 0}) * R0;
g = R0 * g;
//Matrix3d rot_diff = R0 * Rs[0].transpose();
Matrix3d rot_diff = R0;
//目前的Ps,Rs,Vs都是在$c_x$系下的表達,將它們轉換到參考坐標系。
for (int i = 0; i <= frame_count; i++)
{
Ps[i] = rot_diff * Ps[i];
Rs[i] = rot_diff * Rs[i];
Vs[i] = rot_diff * Vs[i];
}
