在學概率論時,常常會看到各種稀奇古怪的名字,有的書上只介紹了該如何求解,但是從不介紹為什么這么叫以及有什么用,本文就介紹一下概率密度估計是什么以及是干什么用的,主要參考Jason BrownLee大神的一篇博文進行介紹。
后面部分名詞會以英文縮寫形式介紹,匯總如下:
- 概率密度 (probability density, PD)
- 概率密度函數 (probability density function, PDF)
- 概率密度估計 (probability density estimation, PDE)
PD&PDF&PDE之間的關系
一句話概括概率密度就是: 概率密度是觀測值與其概率之間的關系
一個隨機變量的某個結果可能會以很低的概率出現,而其他的結果可能概率會比較高。
概率密度的總體形狀被稱為概率分布 (probability distribution),常見的概率分布有均勻分布、正態分布、指數分布等名稱。對隨機變量特定結果的概率計算是通過概率密度函數來完成的,簡稱為PDF (Probability Dense Function)。
那么概率密度函數有什么用呢?很有用!例如我們可以通過PDF來判斷一個樣本的可信度高低,進而判斷這個樣本是否是異常值。另外有時我們的輸入數據如果要服從某個分布也需要用到PDF。
但是通常我們是不知道一個隨機變量的PDF的,因此我們需要不斷去逼近這個PDF,而逼近的這個過程就是概率密度估計。
在對隨機變量進行密度估計的過程中,需要執行幾個步驟。
第一步是用一個簡單的直方圖來檢查隨機樣本中觀測值的密度。從直方圖中,我們可以識別出一個常見的、易於理解的可用概率分布,例如正態分布。如果分布很復雜,我們可能需要擬合一個模型來估計分布。
在接下來的小節中,我們將依次仔細介紹這些步驟。
為了簡單起見,我們將重點介紹單變量數據,例如一個隨機變量。雖然這些步驟適用於多元數據,但隨着變量數量的增加,它們會變得更具挑戰性。
密度直方圖
直方圖是這樣一種圖,它首先將觀察結果分組到各個箱子(bin)中,然后計算每個箱子中的事件數量。每個箱子里的計數或觀察頻率然后用條形圖表示,箱子在x軸上,頻率在y軸上。
箱子數量和大小的設置也是有講究的。比如說觀察值的范圍是1到100,那么我們可以有如下兩種方式的划分:
- 3個箱子 (1-33,34-66,67-100):划分比較粗粒度
- 10個箱子 (1-10,11-20,...,91-100):划分更加細膩度,能更好提取密度信息,但是計算量會更大一些
用python來實現一下正態分布的效果
# example of plotting a histogram of a random sample
from matplotlib import pyplot
from numpy.random import normal
# generate a sample
sample = normal(size=1000)
# plot a histogram of the sample
pyplot.hist(sample, bins=10)
pyplot.show()
pyplot.hist(sample, bins=3)
pyplot.show()
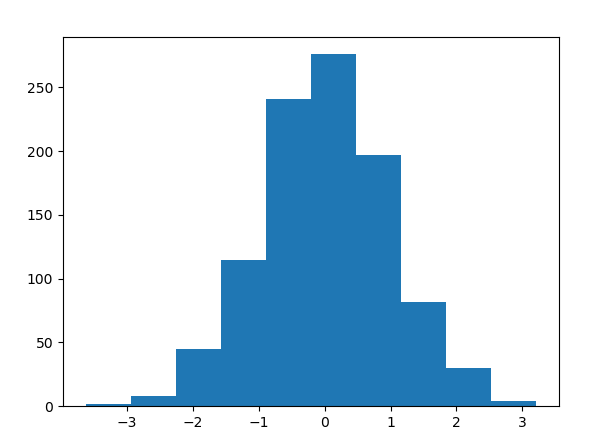
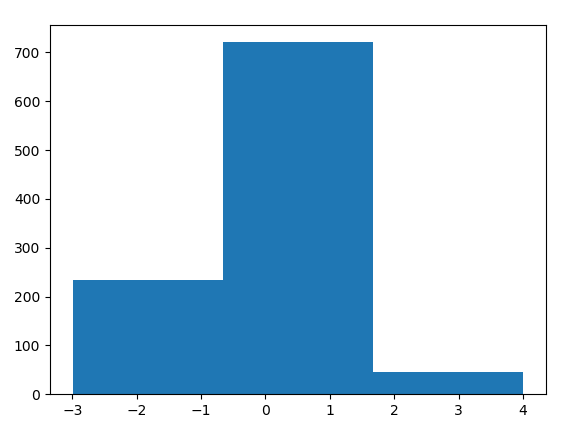
結果如下:(左邊為bin=10,右邊為bin=3)
參數密度估計
大多數隨機樣本的直方圖形狀都會與一些大家都熟知的概率分布相匹配。因為這些概率分布經常會在在不同的或者是意料之外的場景反復出現。熟悉這些常見的概率分布將幫助我們從直方圖中識別對應的分布。一旦我們確認直方圖服從某個已知分布,那么我們接下來要做的事情就是去估計這個分布的參數,所以叫做參數密度估計
例如上面的例子中,我們看左邊的直方圖可以大致猜測其服從正態分布,因此后面只需要求出這個正態分布即可。另外我們知道正態分布只由兩個參數決定(假設是單變量情況),即均值和方差,因此我們通過求出觀測值的均值和方差,我們便求解出了這個直方圖所對應的概率密度函數的估計。
實現代碼和效果圖如下所示:
# example of parametric probability density estimation
from matplotlib import pyplot
from numpy.random import normal
from numpy import mean
from numpy import std
from scipy.stats import norm
# generate a sample
sample = normal(loc=50, scale=5, size=1000)
# calculate parameters
sample_mean = mean(sample)
sample_std = std(sample)
print('Mean=%.3f, Standard Deviation=%.3f' % (sample_mean, sample_std))
# define the distribution
dist = norm(sample_mean, sample_std)
# sample probabilities for a range of outcomes
values = [value for value in range(30, 70)]
probabilities = [dist.pdf(value) for value in values]
# plot the histogram and pdf
pyplot.hist(sample, bins=10, density=True)
pyplot.plot(values, probabilities)
pyplot.show()
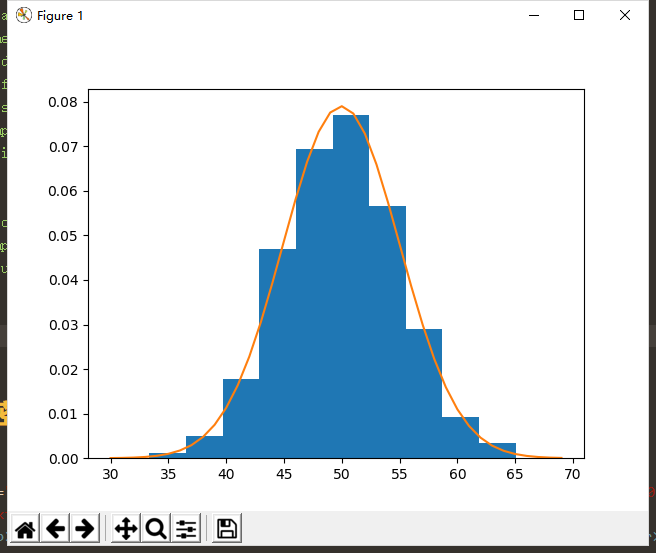
需要注意的是,有的時候我們所觀測到的數據並不顯示地服從某個已知分布,因此通常我們需要先對數據做一定的變換,之后再來做參數密度估計。
- 比如我們需要先對數據做歸一化
- 又或者我們需要先去除一些異常點,因為這些點的存在可能會嚴重影響后面的密度估計
- 當我們的數據明顯左偏(或者右偏)的時候,我們可以對數據取對數或平方根,或者更一般地,使用power轉換(如Box-Cox轉換)。
參數密度估計的步驟總結如下:
Loop Until Fit of Distribution to Data is Good Enough:
- Estimating distribution parameters
- Reviewing the resulting PDF against the data
- Transforming the data to better fit the distribution
非參數密度估計
在某些情況下,一個數據樣本可能不像一個常見的概率分布,或者不容易用某種分布來進行擬合。尤其是當數據有兩個峰(雙峰分布)或多個峰(多峰分布)時,常常會出現這種情況。這種情況下參數密度估計變得不好使,所以非參數密度估計登場了。
其實非參數密度估計還是有參數的,只不過這個參數和參數密度估計中的參數有所不同。后者的參數是可以直接控制分布情況的,而且參數數量通常是預設好的,例如正態分布的參數就兩個:均值和方差。而非參數密度估計其實是使用所有樣本來進行密度估計,換句話說每個樣本的觀測值都被視為參數。常用的估計連續隨機變量概率密度函數的非參數方法有核平滑 (kernel smoothing),或核密度估計,簡稱KDE (Kernel Density Estimation)。
KDE其實就是一個數學函數,它返回隨機變量給定值的概率。Kernel(核函數)能夠有效地平滑或插值隨機變量結果范圍內的概率,使得概率和等於1。Kernel根據數據樣本的觀測值與請求概率的給定查詢樣本之間的關系或距離,對數據樣本中觀測值的貢獻進行加權。
非參數密度估計有兩個重要參數,分別是
-
平滑參數 (smoothing parameter):這個參數有時也叫帶寬 (bandwidth)。因為我們每次都是基於多個樣本來估計一個新的樣本的概率,因此帶寬其實指的就是我們根據多少樣本來預測新樣本的概率,也可以簡單理解成滑窗大小。 帶寬太大,可能因為損失太多細節而導致粗膩度估計;帶寬太小又可能會因為有太多細節使得不夠平滑,因此不能足夠泛化到其他新的樣本。
-
核函數(kernel):用來控制數據集中樣本對估計新樣本點概率的貢獻的函數。
下面也給出一個例子來從直觀上來理解非參數密度估計。
下面是當我們設置不同bins值時的兩個直方圖。可以看到左邊有兩個峰,右邊只有一個。
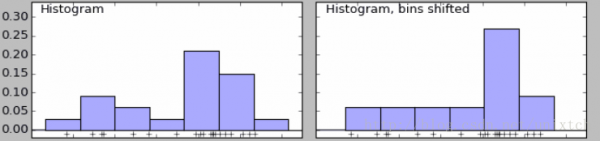
我們也知道當bins增到到樣本的最大值時,就能對樣本的每一點都會有一個屬於自己的概率,但同時會帶來其他問題,樣本中沒出現的值的概率為0,概率密度函數不連續,這同樣存在很大的問題。
核密度函數的原理比較簡單,在我們知道某一事物的概率分布的情況下,如果某一個數在觀察中出現了,我們可以認為這個數的概率密度很大,和這個數比較近的數的概率密度也會比較大,而那些離這個數遠的數的概率密度會比較小。
基於這種想法,針對觀察中的第一個數,我們可以用K去擬合我們想象中的那個遠小近大概率密度。對每一個觀察數擬合出的多個概率密度分布函數,取平均。如果某些數是比較重要的,則可以取加權平均。需要說明的一點是,核密度的估計並不是找到真正的分布函數。
Note: 核密度估計其實就是通過核函數(如高斯)將每個數據點的數據+帶寬當作核函數的參數,得到N個核函數,再線性疊加就形成了核密度的估計函數,歸一化后就是核密度概率密度函數了。
參考:
