這是一次教授布置的期末作業,也是書籍《商務數據分析與應用》的一個課后作業
目錄
數據描述
數據預處理
描述性統計分析
模型分析(方差分析)
數據描述
非學位職業培訓機構的178個學員的數據,目的是了解什么樣的學員可能獲得更好的學習效果
數據預處理
打開數據,查看一部分數據並鎖定數據(這樣之后可以直接使用變量名而不用$來指定數據)
grades=read.table('E:/SWlearning/R/assighment/RegressionAnalysis/Report/ins1.csv',
header=TRUE,sep=',')
head(grades)
attach(grades)
*結果顯示* 
*將變量名改成英文* ``` names(grades)=c('aveGrades','gender','birth','firmType','eduBG','eduGrd')
<br/>
響應變量(因變量):因變量.平均成績(aveGrades)
自變量:性別(gender),出生日期(birth),企業性質(firmType),最高學歷(eduBG),最高學歷畢業時間(eduGrd)
<br/>
*檢查相應變量的正態性*
shapiro.test(aveGrades)
<br/>
*結果顯示*
Shapiro-Wilk normality test
data: aveGrades
W = 0.89736, p-value = 9.286e-10
<br/>
p值非常的小故拒絕原假設,即拒絕數據是正態分布的原假設
<br/>
*接下來用BoxCox的方法,建立新的相應變量從而保證其正態性,注意BoxCox.ar是包TSA里的函數*
library(TSA)
boxcox=BoxCox.ar(aveGrades,lambda = seq(4, 8, 0.1))
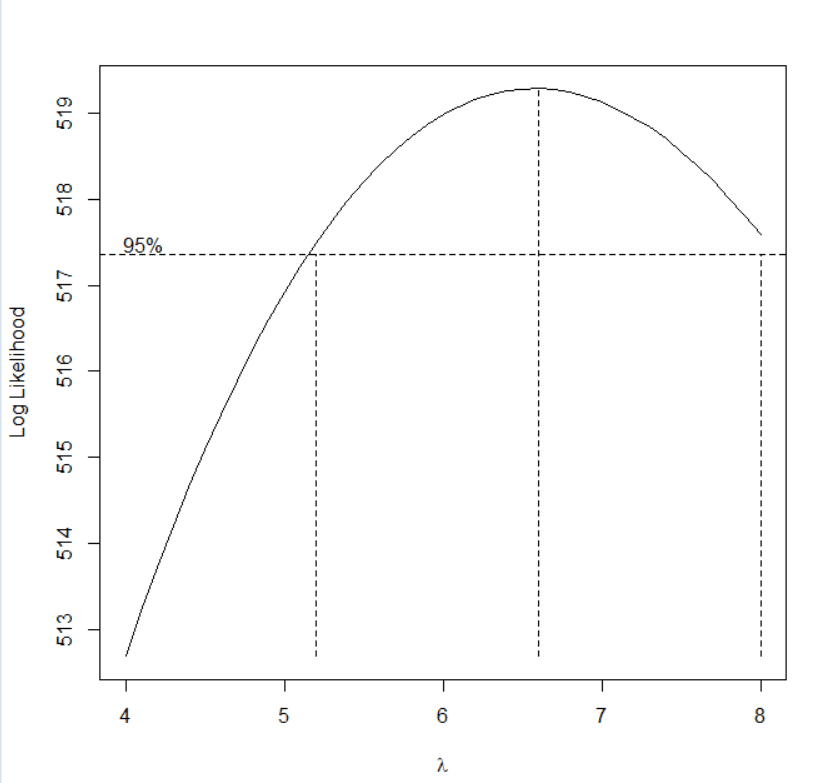
<br/>
*查看最優的lamda值*
boxcox$mle

<br/>
*建立新的響應變量*
aveGrades_mod=grades$aveGrades^6.6
<br/>
*檢驗新的響應變量的正態性*
shapiro.test(aveGrades_mod)
<br/>
*結果顯示*
Shapiro-Wilk normality test
data: aveGrades_mod
W = 0.99007, p-value = 0.2522
<br/>
p值達到了我們期望的結果,不拒絕原假設,即接受新的響應變量是正態分布的假設
<br/>
#描述性統計分析
<br/>
*注意我們的因變量中,出生日期(birth)和最高學歷畢業時間(eduGrd)不是離散變量,我們將以十年的單位將這兩個變量分類
出生日期(birth)中最大是 1952-6-26,最小是 1979-11-10,分成五十年代(1),六十年代(2), 七十年代(3)
最高學歷畢業時間(eduGrd)中最大是 1982-1-1,最小是 2004-3-1,分為八十年代(1),九十年代(2), 零零后(3)*
<br/>
*第一步
將出生日期(birth)和最高學歷畢業時間(eduGrd)變成日期型變量以便之后的操作*
birthmod=as.Date(grades$birth)
eduGrdmod=as.Date(grades$eduGrd)
<br/>
*第二步
我們先對出生年月進行分類*
//d1~d4分別是四個時間節點,用來將數據分成五十年代(1),六十年代(2), 七十年代(3)
d1=as.Date('1950/1/1')
d2=as.Date('1960/1/1')
d3=as.Date('1970/1/1')
d4=as.Date('1980/1/1')
//計算出生日期(birthmod)中的數據個數
s=0
for(i in birthmod){
s=s+1
}
//建立新的數值型變量。因為birthmod是日期型變量,不能直接賦數值型的值如1,2,3
birth_mod=1:s
//開始分類
for(i in 1:s){
fac1=birthmod[i]-d1>0 & birthmod[i]-d2<=0
fac2=birthmod[i]-d2>0 & birthmod[i]-d3<=0
fac3=birthmod[i]-d3>0 & birthmod[i]-d4<=0
if(fac1){birth_mod[i]=1}
if(fac2){birth_mod[i]=2}
if(fac3){birth_mod[i]=3}
}
//給新變量birth_mod三個水平1,2,3
levels(birth_mod)=c(1,2,3)
//將數據類型變成factor,以便之后的統計
birth_mod=as.factor(birth_mod)
<br/>
*對最高學歷畢業時間是同樣的程序*
d5=as.Date('1990/1/1')
d6=as.Date('2000/1/1')
d7=as.Date('2010/1/1')
s=0
for(i in eduGrdmod){
s=s+1
}
eduGrd_mod=1:s
for(i in 1:s){
fac3=eduGrdmod[i]-d4>0 & eduGrdmod[i]-d5<=0;fac3
fac4=eduGrdmod[i]-d5>0 & eduGrdmod[i]-d6<=0;fac4
fac5=eduGrdmod[i]-d6>0 & eduGrdmod[i]-d7<=0;fac5
if(fac3){eduGrd_mod[i]=1}
if(fac4){eduGrd_mod[i]=2}
if(fac5){eduGrd_mod[i]=3}
}
levels(eduGrd_mod)=c(1,2,3)
eduGrd_mod=as.factor(eduGrd_mod)
<br/>
*第三步
建立新的數據集grades_mod,注意此處的響應變量(aveGrades)沒有用之前為了正態性修改的新的響應變量(aveGrades_mod),這里用aveGrades是為了結果好看,且不影響我們進行描述性統計分析*
grades_mod=cbind(grades$aveGrades,grades[2],birth_mod,grades[4:5],eduGrd_mod)
summary(grades_mod)
*結果顯示*
grades$aveGrades gender birth_mod firmType eduBG eduGrd_mod
Min. :50.00 男:133 1:10 國企:95 本科 :148 1: 48
1st Qu.:77.00 女: 45 2:85 民企:43 大專 : 25 2:104
Median :81.00 3:83 外企:40 碩士 : 2 3: 26
Mean :79.72 碩士或以上: 3
3rd Qu.:84.00
Max. :91.00
<br/>
*第四步
我們還想知道,各個因變量不同水平對應的學員平均成績*
//編寫一個輸出均值,標准差,最大值,中位數,最小值的函數
stats = function(x){
m = mean(x)
sd= sd(x)
max = max(x)
median = median(x)
min= min(x)
return=c(m,sd,max,median,min)
}
//aggregate是一個重新顯示數據的函數,比如在aggdata1中,能顯示按性別分類后,男性學員和女性學員對應的平均成績的均值,標准差,最大值,中位數,最小值,FUN是function函數的意思
aggdata1= aggregate(grades['aveGrades'],
by=list(gender),FUN=stats);aggdata1
aggdata2= aggregate(grades['aveGrades'],
by=list(birth_mod),FUN=stats)
aggdata3= aggregate(grades['aveGrades'],
by=list(firmType),FUN=stats)
aggdata4= aggregate(grades['aveGrades'],
by=list(eduBG),FUN=stats);aggdata
aggdata5= aggregate(grades['aveGrades'],
by=list(eduGrd_mod),FUN=stats)
//按行將數據重疊起來
aggdata=rbind(aggdata1,aggdata2,aggdata3,aggdata4,aggdata5);aggdata
<br/>
*結果顯示*
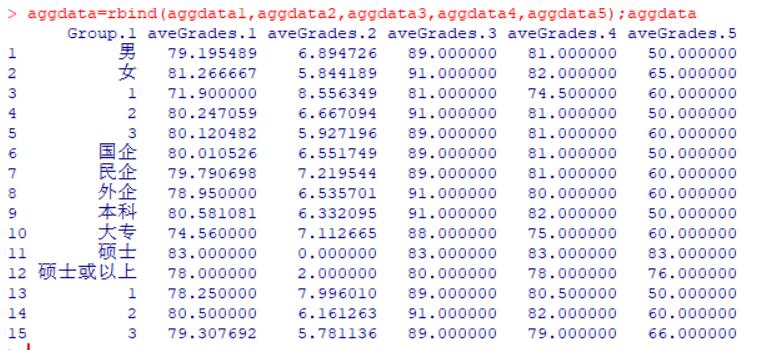
<br/>
#模型分析
*接下來我們將進行方差分析*
*第一步*
//進行方差分析的函數是aov,前面是響應變量,注意此時我們得保證響應變量的正態性,所以用的是新的響應變量(aveGrades_mod)而非原始數據,后面是自變量,在此模型中還包括了所有的交互項
res.ano1=aov(aveGrades_mod~gender+birth_mod+firmType+eduBG+eduGrd_mod+
gender:birth_mod+gender:firmType+gender:eduBG+gender:eduGrd_mod+
birth_mod:firmType+birth_mod:eduBG+birth_mod:eduGrd_mod+
firmType:eduBG+firmType:eduGrd_mod+
eduBG:eduGrd_mod)
//顯示方差分析結果
res1=summary(res.ano1);res1
<br/>
*結果顯示*

<br/>
*第二步
剔除沒通過顯著性檢驗的變量, 用剩下的變量再做一次方差分析*
res.ano2=aov(aveGrades_mod~gender+birth_mod+eduBG+
gender:firmType+gender:eduGrd_mod+
birth_mod:firmType+
firmType:eduBG)
res2=summary(res.ano2);res2
<br/>
*結果顯示*
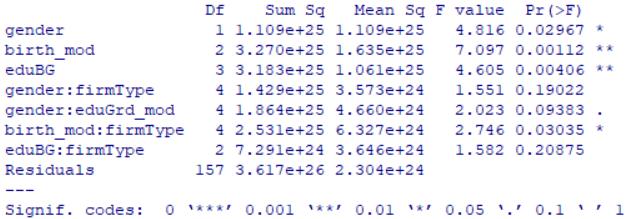
<br/>
*第三步
剔除沒通過顯著性檢驗的變量, 用剩下的變量再做一次方差分析*
res.ano3=aov(aveGrades_mod~gender+birth_mod+eduBG+
gender:eduGrd_mod+
birth_mod:firmType)
res3=summary(res.ano3);res3
<br/>
*結果顯示*
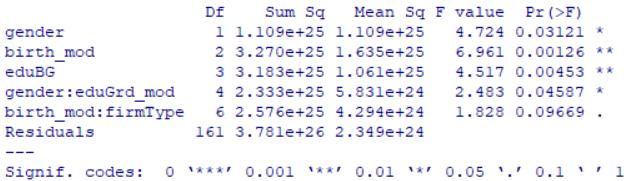
<br/>
性別(gender),出生日期(birth_mod),最高學歷(eduBG)以及交互作用, 性別:最高學歷畢業日期(gender:eduGrd_mod),出生日期:企業性質(birth_mod:firmType)都通過了在 0.1 水平下的顯著性檢驗
拒絕原假設,即變量的水平不同會顯著影響成績,如性別中,男生和女生的成績顯著不同,而企業性質的不同不影響學員的成績