數據結構與算法之圖

圖

定義：圖由邊的集合及頂點的集合組成。頂點也有權重， 也稱為成本。

如果一個圖的頂點對是有序的， 則可以稱之為有向圖。在對有向圖中的頂點對排序后， 便可以在兩
個頂點之間繪制一個箭頭。 有向圖表明了頂點的流向。

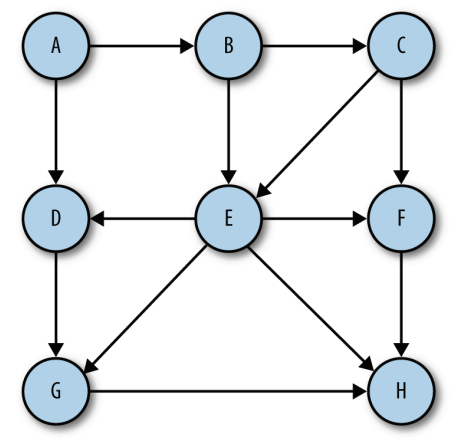
如果圖是無序的， 則稱之為無序圖， 或無向圖。

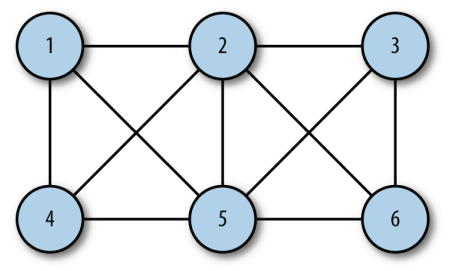
圖中的一系列頂點構成路徑， 路徑中所有的頂點都由邊連接。 路徑的長度用路徑中第一個頂點到最后一個頂點之間邊的數量表示。 由指向自身的頂點組成的路徑稱為環， 環的長度為 0。

圈是至少有一條邊的路徑， 且路徑的第一個頂點和最后一個頂點相同。 無論是有向圖還是無向圖， 只要是沒有重復邊或重復頂點的圈， 就是一個簡單圈。 除了第一個和最后一個頂點以外， 路徑的其他頂點有重復的圈稱為平凡圈。

如果兩個頂點之間有路徑， 那么這兩個頂點就是強連通的， 反之亦然。 如果有向圖的所有的頂點都是強連通的， 那么這個有向圖也是強連通的。

表示頂點

用Vertex類表示節點，Vertex 類有兩個數據成員： 一個用於標識頂點， 另一個是表明這個頂點是否被訪問過的布爾值。它們分別被命名為 label 和 wasVisited。

function Vertex(label){
    this.label = label;
}

表示邊

用鄰接表或鄰接表數組來表示邊。數組的索引表示頂點，元素是一個數組，里面的成員是與該頂點相連的其他頂點。因此鄰接表是一個二維的數組。

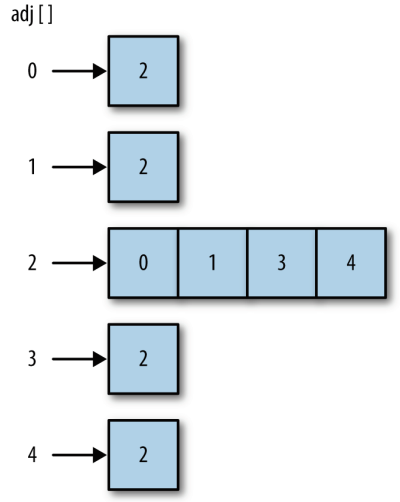
構建圖與搜索圖

搜索圖分兩種方式：深度優先和廣度優先。

廣度優先搜索算法：數據結構是隊列。通過將頂點存入隊列中，最先入隊列的頂點先被探索。
深度優先搜索算法：數據結構是棧。通過將頂點存入棧中，沿着路徑探索頂點，存在新的相鄰頂點就去訪問。

深度優先

深度優先搜索包括從一條路徑的起始頂點開始追溯， 直到到達最后一個頂點， 然后回溯，繼續追溯下一條路徑， 直到到達最后的頂點， 如此往復， 直到沒有路徑為止。

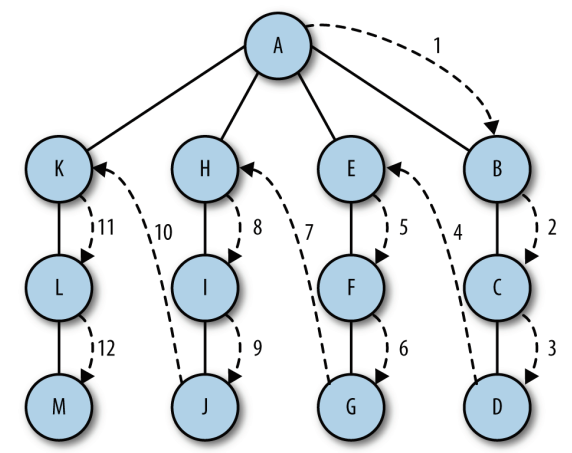
思路：訪問一個沒有訪問過的頂點， 將它標記為已訪問， 再遞歸地去訪問在初始頂點的鄰接表中其他沒有訪問過的頂點。

廣度優先

廣度優先搜索從第一個頂點開始， 嘗試訪問盡可能靠近它的頂點。 本質上， 這種搜索在圖上是逐層移動的， 首先檢查最靠近第一個頂點的層， 再逐漸向下移動到離起始頂點最遠的層。

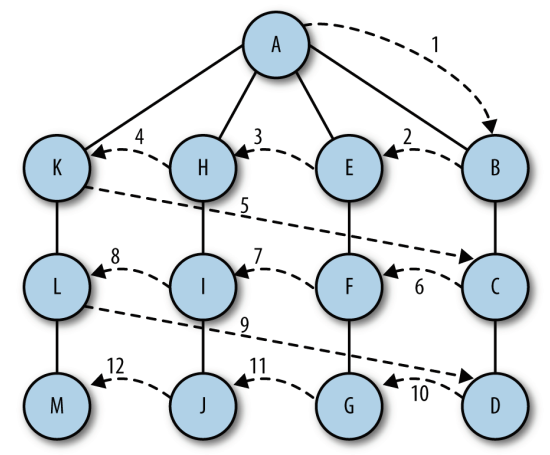
用JS實現以上兩種搜索方法：

// 創建圖類
function Graph(v){
    this.vertices = v;  // 共有多少個節點
    this.edges = 0;  // 有多少條邊
    this.adj = [];  // 鄰接表數組
    for(var i = 0;i<this.vertices;i++){
        this.adj[i] = [];
    }
    this.marked = [];  // 用於搜索
    for(var i = 0;i<this.vertices;i++){
        this.marked[i] = false;
    }
    this.edgeTo = [];  // 用於廣度優先搜索查找最短路徑

}
Graph.prototype = {
    constructor: Graph,

    // 在兩個頂點間畫一條邊
    addEdge(v, w){
        this.adj[v].push(w);
        this.adj[w].push(v);
        this.edges++;
    },
    showGraph(){
        for(var i = 0;i<this.vertices;i++){
            var str = '';
            for(var j = 0;j<this.vertices;j++){
                if(this.adj[i][j] !== undefined){
                    str += this.adj[i][j] + ' ';
                }
            }
            console.log(i + "-> " + str + '\n');
        }
    },

    // 深度優先搜索函數depth first searching，遞歸實現
    dfs(v){
        this.marked[v] = true;
        if(this.adj[v].length){
            console.log("Visited vertex: " + v);
            for(var w of this.adj[v]){
                if(!this.marked[w]){
                    this.dfs(w);
                }
            }
        }
    },

    // 廣度優先搜索函數，無遞歸實現
    bfs(s){
        var queue = [];
        this.marked[s] = true;
        queue.push(s);
        while(queue.length > 0){
            var v = queue.shift();
            console.log("Visited vertex: " + v);
            for(var w of this.adj[v]){
                if(!this.marked[w]){
                    this.edgeTo[w] = v; 
                    this.marked[w] = true;
                    queue.push(w);
                }
            }                            
        }
    }
}

利用廣度優先搜索方法查找最短路徑（查找頂點1和頂點4之間的最短路徑）：

需要再擴展一個方法，通過執行一次廣度優先搜索后得到的edgeTo數組來找到1和4節點之間相互連接的節點：

Graph.prototype.pathTo = function(w, v){
    this.bfs(w);
    var source = w;  // 頂點w作為起點
    if(!this.hasPathTo(v)){
        return undefined;
    }
    var path = [];  // 保存路徑，不過是從終點到起點的
    for(var i = v; i != source; i = this.edgeTo[i]){
        path.push(i);
    }
    path.push(source);
    return path;
}
Graph.prototype.hasPathTo(v){
    return this.marked[v];
}

var g = new Graph(6);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 5);
g.addEdge(2, 3);
g.addEdge(3, 5);
g.addEdge(2, 4);
g.showGraph();
g.pathTo(4, 1);  // [1, 0, 2, 4]