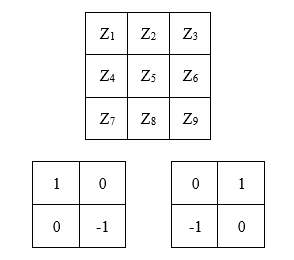
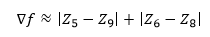線性平滑濾波之均值濾波
用一個像素的鄰域的平均值作為濾波結果,首先選擇一個n*n的奇數模板,如3*3模板。
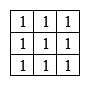
將模板中心點對准需要濾波的圖像像素點,在算得卷積值后除以n\*n,結果作為濾波結果即可。模板尺寸變大平滑效果越好,但同時會給圖像帶來模糊的效果並且增大了運算量,因此需要根據需求選擇合適的模板尺寸,一般采用3\*3模板。 針對離中心近的像素對應濾波結果有較大貢獻,因此可以將普通均值濾波改進為對鄰域平均進行加權的加權均值濾波。如采用以下的3\*3模板來對圖像平滑處理。
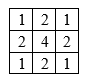
鄰域平均法在一定程度上能夠抑制噪聲,但會引起模糊現象,模糊程度與鄰域半徑成正比。采用超限均值濾波可有效緩解此現象,超限均值濾波是當中心像素值與鄰域像素平均值的差值的絕對值達到一定水平才用均值代替中心像素值。
線性銳化濾波之拉普拉斯算子
拉普拉斯算子是一種二階微分算子,通常在數字圖像處理過程中將差分近似微分。拉普拉斯算子原表達式如下所示:
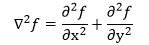
兩個分別沿X和Y方向的二階偏導數的差分近似微分:
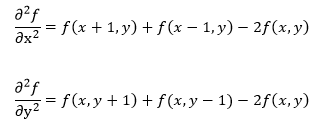
將以上兩式綜合得:
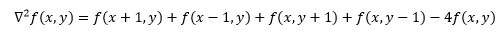
據此可得卷積模板:
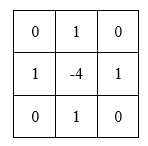
模板在上下左右四個90度的方向上結果相同,也就是說在90度方向上無方向性。為了讓其在45度的方向上也具有該性質,對該模板進行擴展定義為:
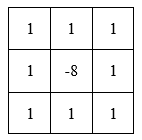
###非線性平滑濾波器之中值濾波器 用一個像素的鄰域的中值作為濾波結果,定義濾波器尺寸為3\*3(一般為奇數)。將模板中心點對准需要濾波的圖像像素點,將像素點與其八鄰域像素值進行排序取中值,用中值替代該像素點的值。 超限中值濾波器和前面的超限均值濾波思想類似,當中心像素值與中值的差值的絕對值達到一定水平才用該中值代替中心點像素值。 ###非線性銳化濾波器之Sobel、Prewitt、Robert濾波器 **Sobel算子**在X、Y方向上的模板如下所示:
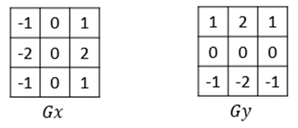
Sobel算子是一階微分算子,其來歷即使是數字圖像處理-剛薩雷斯版也未對其有具體說明,讀者若是想要了解可在互聯網上搜尋《作者40年后談Sobel算子的由來和定義》一文了解。 Sobel算子X、Y方向的卷積計算公式如下:
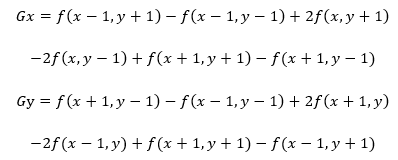
得出Gx和Gy的值后,再求出其梯度值G(x,y)。
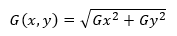
將上式簡化得:
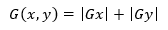
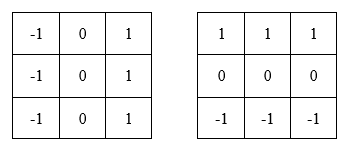
**Prewitt算子**也是一階微分算子,與Sobel不同的是其沒有對像素的位置的影響進行加權,Prewitt算子模板如下所示:
**Robert算子**是交叉梯度算子,梯度計算由兩個模板組成,求出兩個梯度項后求和可得梯度。