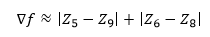线性平滑滤波之均值滤波
用一个像素的邻域的平均值作为滤波结果,首先选择一个n*n的奇数模板,如3*3模板。
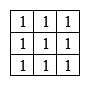
将模板中心点对准需要滤波的图像像素点,在算得卷积值后除以n\*n,结果作为滤波结果即可。模板尺寸变大平滑效果越好,但同时会给图像带来模糊的效果并且增大了运算量,因此需要根据需求选择合适的模板尺寸,一般采用3\*3模板。 针对离中心近的像素对应滤波结果有较大贡献,因此可以将普通均值滤波改进为对邻域平均进行加权的加权均值滤波。如采用以下的3\*3模板来对图像平滑处理。
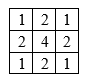
邻域平均法在一定程度上能够抑制噪声,但会引起模糊现象,模糊程度与邻域半径成正比。采用超限均值滤波可有效缓解此现象,超限均值滤波是当中心像素值与邻域像素平均值的差值的绝对值达到一定水平才用均值代替中心像素值。
线性锐化滤波之拉普拉斯算子
拉普拉斯算子是一种二阶微分算子,通常在数字图像处理过程中将差分近似微分。拉普拉斯算子原表达式如下所示:
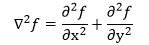
两个分别沿X和Y方向的二阶偏导数的差分近似微分:
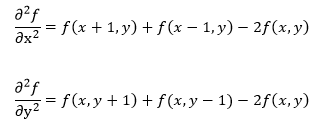
将以上两式综合得:
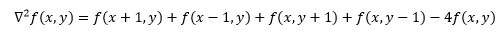
据此可得卷积模板:
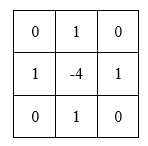
模板在上下左右四个90度的方向上结果相同,也就是说在90度方向上无方向性。为了让其在45度的方向上也具有该性质,对该模板进行扩展定义为:
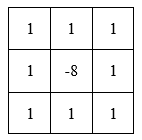
###非线性平滑滤波器之中值滤波器 用一个像素的邻域的中值作为滤波结果,定义滤波器尺寸为3\*3(一般为奇数)。将模板中心点对准需要滤波的图像像素点,将像素点与其八邻域像素值进行排序取中值,用中值替代该像素点的值。 超限中值滤波器和前面的超限均值滤波思想类似,当中心像素值与中值的差值的绝对值达到一定水平才用该中值代替中心点像素值。 ###非线性锐化滤波器之Sobel、Prewitt、Robert滤波器 **Sobel算子**在X、Y方向上的模板如下所示:
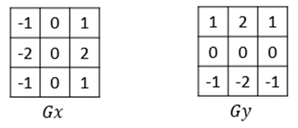
Sobel算子是一阶微分算子,其来历即使是数字图像处理-刚萨雷斯版也未对其有具体说明,读者若是想要了解可在互联网上搜寻《作者40年后谈Sobel算子的由来和定义》一文了解。 Sobel算子X、Y方向的卷积计算公式如下:
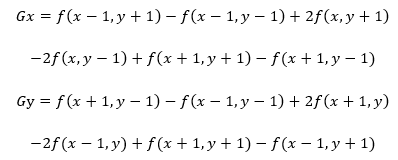
得出Gx和Gy的值后,再求出其梯度值G(x,y)。
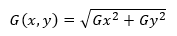
将上式简化得:
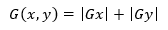
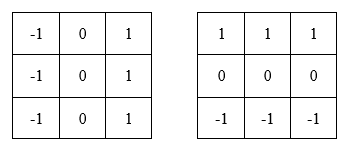
**Prewitt算子**也是一阶微分算子,与Sobel不同的是其没有对像素的位置的影响进行加权,Prewitt算子模板如下所示:
**Robert算子**是交叉梯度算子,梯度计算由两个模板组成,求出两个梯度项后求和可得梯度。