寫在前面
看這篇筆記之前先看一下參考文章,這篇筆記沒有系統的講述矩陣和代碼的東西,參考文章寫的也有錯誤的地方,要辨證的看。
- 如何計算矩陣乘法
- android matrix 最全方法詳解與進階(完整篇)
- Android Matrix 最全方法詳解與進階
- 1-4 Canvas 對繪制的輔助 clipXXX() 和 Matrix
矩陣的乘法
比如有矩陣A和矩陣B,他們分別為:
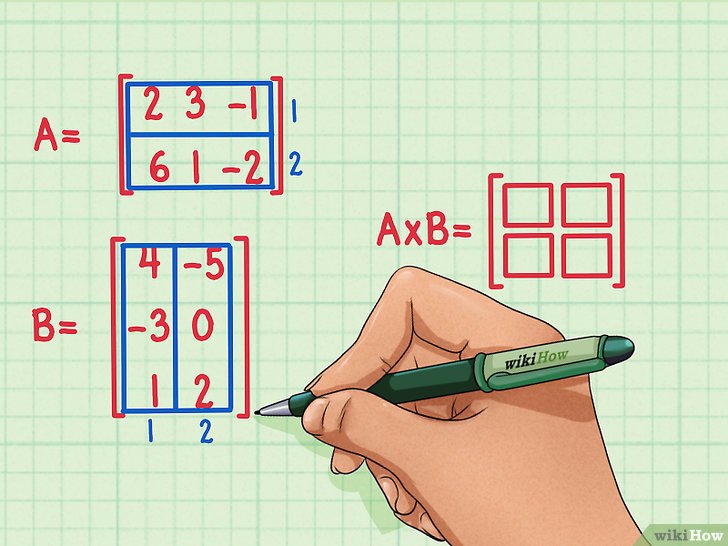
可以看到A為2行3列的矩陣,B為3行2列的矩陣,矩陣乘法符合下面的規則:
- 只有A的列數和B的行數相等,A和B才可以做乘法
- A*B的結果C是2行2列的矩陣,行數等於A的行數,列數等於B的列數
- 結果矩陣C的第一行第一列數值為A的第一行和B的第一列中的數字分別相乘后再相加。其他行列結果依次類推
- 矩陣的乘法不滿足交換律,即
A*B != B*A - 矩陣的乘法滿足結合律
M‘ = T*(M*R) = T*M*R = (T*M)*R
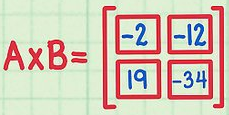
詳細信息可以看這里:如何計算矩陣乘法
Android中常用的四種矩陣變換
Android中使用3x3的矩陣進行圖形的變換,它看起來大概是下面這樣:
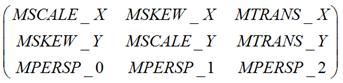
在Android中,使用一個3x1的矩陣來表示一個點:
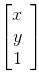
x,y分別代表x,y軸上的坐標,而1代表屏幕在z軸上的坐標為默認的。如果將1變大,那么屏幕會拉遠, 圖形會變小。
平移(Translate)

圖例:

錯切(Skew)
水平錯切

圖例:
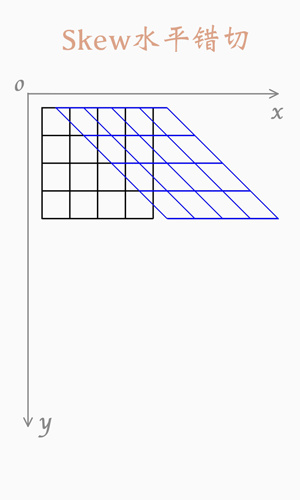
垂直錯切

圖例:

復合錯切

圖例:
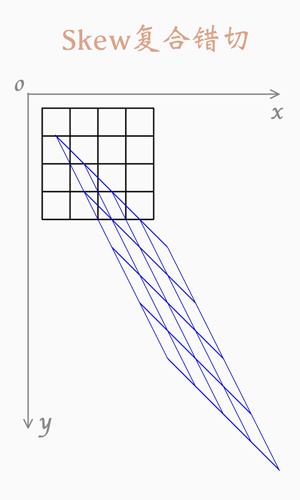
旋轉(Rotate)

圖例:

縮放(Scale)

圖例:
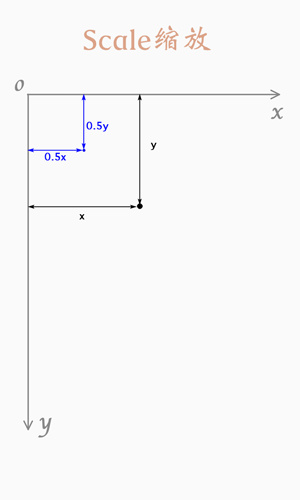
Matrix的組合
應用矩陣進行圖形變換的主要原因,是因為矩陣是可以通過矩陣的乘法進行組合使用的,如果想對canvas繪制的bitmap時,先平移T(dx, dy),再旋轉R(θ),最后縮放S(k1,k2),就可以將三個變換矩陣相乘,M‘ = ABC,再對canvas應用M’矩陣即可。
Matrix的坐標系
矩陣的操作可以看作是以坐標原點為原點的坐標系在三維空間中做的變換,不同於canvas的屏幕坐標系坐標系,矩陣Matrix的坐標系為左手坐標系:
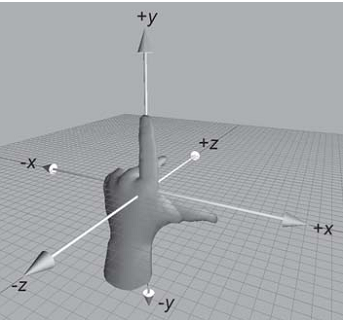
這個坐標系對應的每個軸的旋轉方向(從原點看出去,每個軸的旋轉方向都是逆時針):
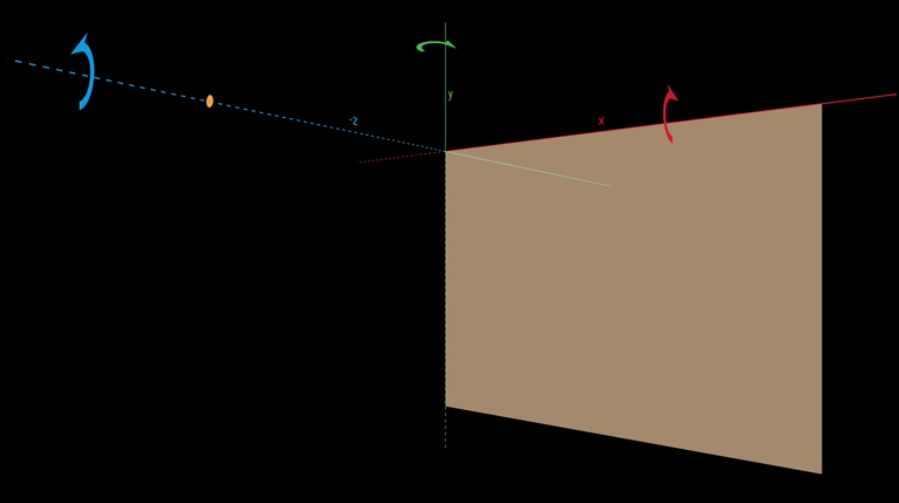
Matrix的操作可以看做是對上面左手坐標系的變換
因為Matrix變換后是對每個canvas的點起作用,其實也可以看做對這個三維坐標系起了作用,canvas繪制的是三維坐標系上的圖像對canvas二位坐標系的投影。
所以,可以用自己的左手模擬進行平移旋轉等操作,更加直觀的想象變換后的效果。
Matrix的左乘和右乘
在Android中,有關矩陣的操作都是成對的,比如preTranslate(float dx, float dy)和postTranslate(float dx, float dy),通過看api的介紹,如果原矩陣為M,那么pre表示的是左乘,post表示右乘:
preTranslate : M' = M * T(dx, dy) // 左乘
postTranslate: M' = T(dx, dy) * M // 右乘
因為矩陣的變換是順序執行的,所以在平時最常用的應該是pre左乘,所有的變換操作都依次執行,比如canvas常用的translate等變換方法其實就是左乘。右乘其實就是在所有操作之前增加一步操作,合理的運用右乘可以方便代碼的編寫。
比如:圖形變換是以左邊原點為原點的,所以旋轉、縮放等功能應用到canvas.drawBitmap()方法時(因為bitmap常從原點往右下方畫),圖像表現出來的結果就特別奇怪,需要將canvas的坐標系移動到圖像的中心點再操作然后再把坐標系移回去,那么如果只用pre左乘的話,代碼是這樣的:
Matrix matrix = new Matrix();
matrix.preTranslate(pivotX,pivotY);
// 各種操作,旋轉,縮放,錯切等,可以執行多次。
matrix.preTranslate(-pivotX, -pivotY);
如果合理使用右乘,那么代碼就成了:
Matrix matrix = new Matrix();
// 各種操作,旋轉,縮放,錯切等,可以執行多次。
matrix.postTranslate(pivotX,pivotY);
matrix.preTranslate(-pivotX, -pivotY);
減少了postTranslate和preTranslate之間的距離。
