---恢復內容開始---
@[toc] # 1 簡述 霍夫變換是一個經典的特征提取技術,本文主要說的是霍夫線/圓變換,即從圖像中獲取直線與圓,同時需要對圖像進行二值化操作,效果如下。 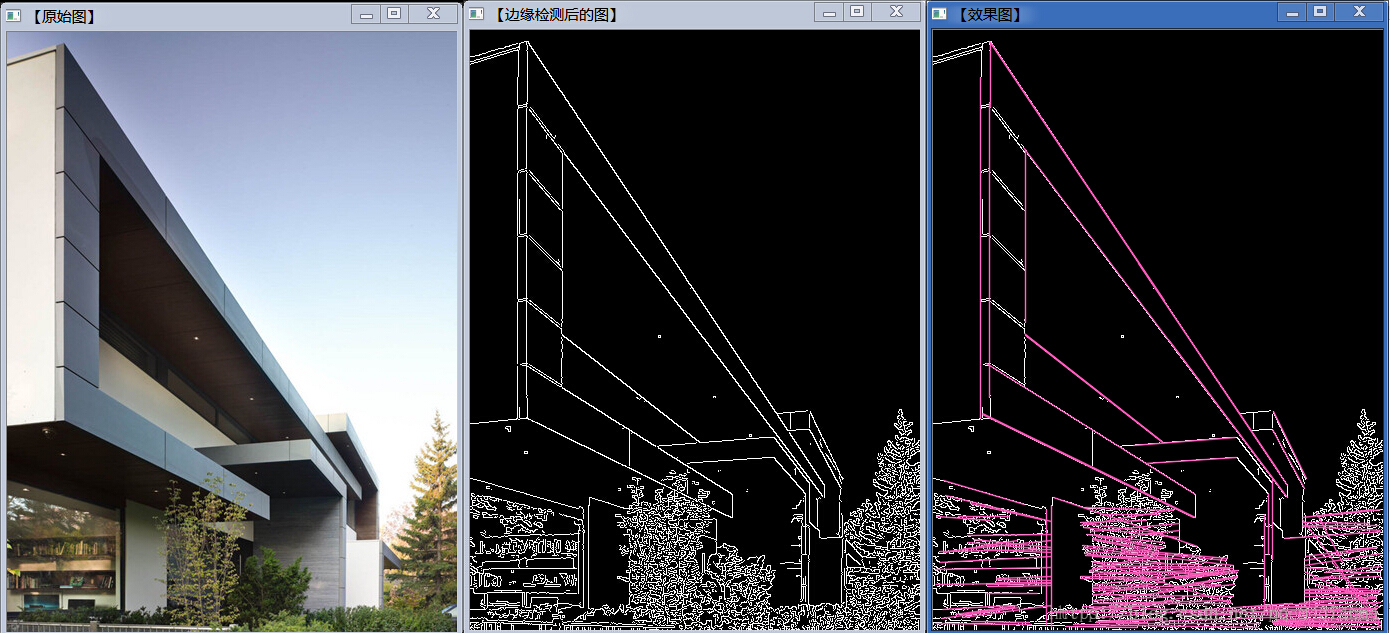 霍夫變換目的通過投票程序在特定類型的形狀內找到對象的不完美示例,這個投票程序是在一個參數空間中進行的,在這個參數空間中,候選對象被當作所謂的累加器空間中的局部最大值來獲得,所述累加器空間由用於計算霍夫變換的算法明確的構建,霍夫變換不僅能夠識別出圖像中有無需要檢測的圖形,而且能夠定位到該圖像(包括位置、角度等),有標准霍夫變換,多尺度霍夫變換,統計概率霍夫變換3種較為經典的方法,主要優點是 能容忍特征邊界描述中的間隙,並且相對不受圖像噪聲的影響。2 標准霍夫線變換原理
2.1 霍夫變換直線的方程
直線的方程形式有截距式,斜截式,一般式,點斜式等,但是這些形式都有“奇異”情況,其中一個截距為0,斜率為0, c=0(通常把c除到等式左面,減少一個參數的搜索),另外某些形式的參數空間不是閉的,比如斜截式的斜率k,取值范圍從0到無窮大,給量化搜索帶來了困難。所以在霍夫線變換中采用了如下方程的形式:
其中\(p\)與\(\theta\)都是極坐標下點的極徑與極角(也可以理解\(p\)是原點離直線最近的距離),但並不是極坐標方程,因為還在笛卡爾坐標下表示,兩個參數的意義如下圖:

這個方程的巧妙之處是角度與距離這兩個參數都是有界的,而且沒有奇異的情況,因此可以在參數空間中進行搜索。同時,直線霍夫變換有2個參數通過這一個等式相關聯,所以程序在投票階段只需要遍歷其中一個,通過等式獲取另一個參數從而進行投票與搜索峰值。
2.2 霍夫空間
對於直線來說,可以將圖像的每一條直線與一對參數\((p, \theta)\)相關聯,這個參數\((p, \theta)\)平面有時被稱為霍夫空間,用於二維直線的集合,因此,對於某一指定的點,不同的\((p, \theta)\)代表了不同的直線,我們把\((p, \theta)\)之間的關系通過圖像表示出來——固定一個點(3,4),角度取[0,2\(\pi\)]時,\(r\)的范圍取值情況:

會發現曲線的形狀類似一條正弦曲線,通常\(p\)越大,正弦曲線的振幅越大,反而就會越小。
2.3 檢測直線的方法
可以得到一個結論,給定平面中的單個點,那么通過該點的所有直線的集合對應於(r,θ)平面中的正弦曲線,這對於該點是獨特的。一組兩個或更多點形成一條直線將產生在該線的(r,θ)處交叉的一條或多條正弦曲線。因此,檢測共線點的問題可以轉化為找到並發曲線的問題。
具體的,通過將霍夫參數空間量化為有限間隔或累加器單元來實現變換。隨着算法的運行,每個算法都把\((x_{i}, y_{i})\)轉換為一個離散化的 \((r,θ)\)曲線,並且沿着這條曲線的累加器單元被遞增。累加器陣列中產生的峰值表示圖像中存在相應的直線的有力證據。 換句話說,將每個交點看成一次投票,也就是說\(A(r,θ)=A(r,θ)+1\),所有點都如此進行計算后,可以設置一個閾值,投票大於這個閾值的可以認為是找到的直線。
2.4 一個例子
舉一個具體的例子,來體現霍夫變換的流程同時更深的理解一下該算法(此例子摘取某博客,下文會給出所有參考博客的鏈接)
霍夫變換可用於識別最適合一組給定邊緣點的曲線的參數。該邊緣描述通常從諸如Roberts Cross,Sobel或 Canny邊緣檢測器的特征檢測算子獲得,並且可能是嘈雜的,即其可能包含對應於單個整體特征的多個邊緣片段。此外,由於邊緣檢測器的輸出僅限定圖像中的特征的位置,所以霍夫變換進一步是確定兩個特征是什么(即檢測其具有參數(或其他)的特征描述)以及 它們有多少個存在於圖像中。
為了詳細說明霍夫變換,我們從兩個閉合矩形的簡單圖像開始。

使用 Canny邊緣檢測器可產生一組邊界描述的這個部分,如下圖:

這里我們看到了圖像中的整體邊界,但是這個結果並沒有告訴我們邊界描述中的特征的身份(和數量)。在這種情況下,我們可以使用Hough(線檢測)變換來檢測該圖像的八個單獨的直線段,從而確定對象的真實幾何結構。
如果我們使用這些邊緣/邊界點作為Hough變換的輸入,每一個點通過遍歷不同的\((r, \theta)\)都會在笛卡爾空間中生成一條曲線,當被視為強度圖像時, 累加器陣列看起來像如下所示:

可以利用直方圖均衡技術使得圖像可以讓我們看到包含在低強度像素值中的信息模式,如下圖:

注意,雖然r和θ是概念上的極坐標,但是累加器空間以橫坐標θ和縱坐標r的矩形繪制 。請注意,累加器空間環繞圖像的垂直邊緣,因此實際上只有8個實際峰值。
由梯度圖像中的共線點生成的曲線(r,θ) 在霍夫變換空間中的峰中相交。這些交點表征原始圖像的直線段。有許多方法可用於從累加器陣列中提取這些亮點或局部最大值。例如,一個簡單的方法涉及閾值處理,然后 對累加器陣列圖像中孤立的亮點集群進行一些細化處理。這里我們使用相對閾值來提取(r,θ) ,對應於原始圖像中的每條直線邊緣的點。(換句話說,我們只采用累加器數組中的那些局部最大值,其值等於或大於全局最大值的某個固定百分比。)
從Hough變換空間(即,反霍夫變換)映射回笛卡爾空間產生一組圖像主題的線描述。通過將該圖像疊加在原始的反轉版本上,我們可以確認霍夫變換找到兩個矩形的8個真實邊的結果,並且因此展示出了遮擋場景的基礎幾何形狀。

請注意,在這個簡單的例子中,檢測到的和原始圖像線的對齊精度顯然不完美,這取決於累加器陣列的量化。(還要注意許多圖像邊緣有幾條檢測線,這是因為有幾個附近的霍夫空間峰值具有相似的線參數值,存在控制這種效應的技術,但這里沒有用來說明標准霍夫變換)
還要注意,由霍夫變換產生的線條的長度是無限的。如果我們希望識別產生變換參數的實際線段,則需要進一步的圖像分析以便查看這些無限長線的哪些部分實際上具有點。
為了說明Hough技術對噪聲的魯棒性,Canny邊緣描述已被破壞1%(由椒鹽噪聲引起), 在Hough變換之前,如圖12所示。

霍夫空間如下圖所示:

將這個結果反霍夫變換(相對閾值設置為40%,並將它覆蓋在原來的結果上)

可以通過變換圖像來研究Hough變換對特征邊界中的間隙的敏感性,如下圖:

然后我們再將其變換到霍夫變換空間,如下圖

然后使用40%的相對閾值去對圖像反霍夫變換(同樣也是疊加在原圖上)

在這種情況下,因為累加器空間沒有接收到前面例子中的條目數量,只能找到7個峰值,但這些都是結構相關的線。
3 霍夫線變換的算法流程
3.1 標准霍夫線變換算法流程
- 讀取原始圖像,並轉換成灰度圖,利用閾值分割或者邊緣檢測算子轉換成二值化邊緣圖像
- 初始化霍夫空間, 令所有\(Num(\theta, p) = 0\)
- 對於每一個像素點\((x, y)\),在參數空間中找出所有滿足\(xcos\theta + ysin\theta = p\)的\((\theta, p)\)對,然后令\(Num(\theta, p) = Num(\theta, p) + 1\)
- 統計所有\(Num(\theta, p)\)的大小,取出\(Num(\theta, p) > τ\)的參數(\(τ\)是所設的閾值),從而得到一條直線。
- 將上述流程取出的直線,確定與其相關線段的起始點與終止點(有一些算法,如蝴蝶形狀寬度,峰值走廊之類)
3.2 統計概率霍夫變換算法流程
標准霍夫變換本質上是把圖像映射到它的參數空間上,它需要計算所有的M個邊緣點,這樣它的運算量和所需內存空間都會很大。如果在輸入圖像中只是處理\(m(m<M)\)個邊緣點,則這m個邊緣點的選取是具有一定概率性的,因此該方法被稱為概率霍夫變換(Probabilistic Hough Transform)。該方法還有一個重要的特點就是能夠檢測出線端,即能夠檢測出圖像中直線的兩個端點,確切地定位圖像中的直線。
HoughLinesP函數就是利用概率霍夫變換來檢測直線的。它的一般步驟為:
- 隨機抽取圖像中的一個特征點,即邊緣點,如果該點已經被標定為是某一條直線上的點,則繼續在剩下的邊緣點中隨機抽取一個邊緣點,直到所有邊緣點都抽取完了為止;
- 對該點進行霍夫變換,並進行累加和計算;
- 選取在霍夫空間內值最大的點,如果該點大於閾值的,則進行步驟4,否則回到步驟1;
- 根據霍夫變換得到的最大值,從該點出發,沿着直線的方向位移,從而找到直線的兩個端點;
- 計算直線的長度,如果大於某個閾值,則被認為是好的直線輸出,回到步驟1。
4 OpenCV中的霍夫變換函數
4.1標准霍夫變換HoughLines()函數
void HoughLines(InputArray image,OutputArray lines, double rho,
double theta, int threshold, double srn=0,double stn=0 )
第一個參數,InputArray類型的image,輸入圖像,即源圖像,需為8位的單通道二進制圖像,可以將任意的源圖載入進來后由函數修改成此格式后,再填在這里。
第二個參數,InputArray類型的lines,經過調用HoughLines函數后儲存了霍夫線變換檢測到線條的輸出矢量。每一條線由具有兩個元素的矢量\((p, \theta)\)表示,其中,\(p\)是離坐標原點((0,0)(也就是圖像的左上角)的距離。 \(\theta\)是弧度線條旋轉角度(0~垂直線,π/2~水平線)。
第三個參數,double類型的rho,以像素為單位的距離精度。另一種形容方式是直線搜索時的進步尺寸的單位半徑。PS:Latex中/rho就表示 \(\rho\)。
第四個參數,double類型的theta,以弧度為單位的角度精度。另一種形容方式是直線搜索時的進步尺寸的單位角度。
第五個參數,int類型的threshold,累加平面的閾值參數,即識別某部分為圖中的一條直線時它在累加平面中必須達到的值。大於閾值threshold的線段才可以被檢測通過並返回到結果中。
第六個參數,double類型的srn,有默認值0。對於多尺度的霍夫變換,這是第三個參數進步尺寸rho的除數距離。粗略的累加器進步尺寸直接是第三個參數rho,而精確的累加器進步尺寸為rho/srn。
第七個參數,double類型的stn,有默認值0,對於多尺度霍夫變換,srn表示第四個參數進步尺寸的單位角度theta的除數距離。且如果srn和stn同時為0,就表示使用經典的霍夫變換。否則,這兩個參數應該都為正數。
4.2 統計概率霍夫變換(HoughLinesP)
C++: void HoughLinesP(InputArray image, OutputArray lines,
double rho, double theta, int threshold, double minLineLength=0, double maxLineGap=0 )
第一個參數,InputArray類型的image,輸入圖像,即源圖像,需為8位的單通道二進制圖像,可以將任意的源圖載入進來后由函數修改成此格式后,再填在這里。
第二個參數,InputArray類型的lines,經過調用HoughLinesP函數后后存儲了檢測到的線條的輸出矢量,每一條線由具有四個元素的矢量\((x_1,y_1, x_2, y_2)\)表示,其中,\((x_1, y_1)\)和\((x_2, y_2)\)是每個檢測到的線段的結束點。
第三個參數,double類型的rho,以像素為單位的距離精度。另一種形容方式是直線搜索時的進步尺寸的單位半徑。
第四個參數,double類型的theta,以弧度為單位的角度精度。另一種形容方式是直線搜索時的進步尺寸的單位角度。
第五個參數,int類型的threshold,累加平面的閾值參數,即識別某部分為圖中的一條直線時它在累加平面中必須達到的值。大於閾值threshold的線段才可以被檢測通過並返回到結果中。
第六個參數,double類型的minLineLength,有默認值0,表示最低線段的長度,比這個設定參數短的線段就不能被顯現出來。
第七個參數,double類型的maxLineGap,有默認值0,允許將同一行點與點之間連接起來的最大的距離。
5 源碼分析
此部分參考幾位博主的博客,更改了里面一些我認為不太對的地方以及加上了一些自己的理解還有就是一些沒有解釋的地方
5.1 HoughLines()源碼分析
閱讀源碼之后,發現源碼確實細節方面做得比較好,無論是內存方面,還是效率方面,包括一些小細節,比如避免除法,等等。所以源碼值得借鑒與反復參考,具體解釋如下。
static void icvHoughLinesStandard( const CvMat* img, float rho, float theta, int threshold, CvSeq *lines, int lineMax)
{
cv::AutoBuffer<int> _accum, _sort_buf;
cv::AutoBuffer<float> _tabSin, _tabCos;
const uchar* image;
int step, width, height;
int numangle, numrho;
int total=0;
float ang;
int r, n;
int i, j;
float irho = 1 / rho;
double scale;
//再次確保輸入圖像的正確性
CV_Assert( CV_IS_MAT(img) && CV_MAT_TYPE(img->type) == CV_8UC1);
image = img->data.ptr; //得到圖像的指針
step = img->step; //得到圖像的步長(通道)
width = img->cols; //得到圖像的寬
height = img->rows; //得到圖像的高
//由角度和距離的分辨率得到角度和距離的數量,即霍夫變換后角度和距離的個數
numangle = cvRound(CV_PI / theta); // 霍夫空間,角度方向的大小
numrho = cvRound(((width + height)*2 + 1) / rho); //r的空間范圍, 這里以周長作為rho的上界
/*
allocator類是一個模板類,定義在頭文件memory中,用於內存的分配、釋放、管理,它幫助我們將內存分配和對象構造分離開來。具體地說,allocator類將內存的分配和對象的構造解耦,
分別用allocate和construct兩個函數完成,同樣將內存的釋放和對象的析構銷毀解耦,分別用deallocate和destroy函數完成。
*/
//為累加器數組分配內存空間
//該累加器數組其實就是霍夫空間,它是用一維數組表示二維空間
_accum.allocate((numangle+2) * (numrho + 2));
//為排序數組分配內存空間
_sort_buf.allocate(numangle * numrho);
//為正弦和余弦列表分配內存空間
_tabSin.allocate(numangle);
_tabCos.allocate(numangle);
//分別定義上述內存空間的地址指針
int *accum = _accum, *sort_buf = _sort_buf;
int *tabSin = _tabSin, *tabCos = _tabCos;
//累加器數組清零
memset( accum, 0, sizeof(accum[0]) * (numangle+2) * (numrho+2) );
//為避免重復運算,事先計算好sinθi/ρ和cosθi/ρ
for( ang = 0, n = 0; n < numangle; ang += theta, n++ ) //計算正弦曲線的准備工作,查表
{
tabSin[n] = (float)(sin(ang) * irho);
tabCos[n] = (float)(cos(ang) * irho);
}
//stage 1. fill accumulator
//執行步驟1,逐點進行霍夫空間變換,並把結果放入累加器數組內
for( i = 0 ; i < height; i++)
for( j = 0; j < width; j++)
{
//只對圖像的非零值處理,即只對圖像的邊緣像素進行霍夫變換
if( image[i * step + j] != 0 ) //將每個非零點,轉換為霍夫空間的離散正弦曲線,並統計。
for( n = 0; n < numangle; n++ )
{
//根據公式: ρ = xcosθ + ysinθ
//cvRound()函數:四舍五入
r = cvRound( j * tabCos[n] + i * tabSin[n]);
//numrho是ρ的最大值,或者說最大取值范圍
r += (numrho - 1) / 2; //因為theta是從0到π的,所以cos(theta)是有負的,所以就所有的r += 最大值的一半,讓極徑都>0
//另一方面,這也預防了r小於0,讓本屬於這一行的點跑到了上一行,這樣可能導致同一個位置卻表示了多個不同的“點”
//r表示的是距離,n表示的是角點,在累加器內找到它們所對應的位置(即霍夫空間內的位置),其值加1
accum[(n+1) * (numrho+2)+ r + 1]++;
/*
將1維數組想象成2維數組
n+1是為了第一行空出來
numrho+2 是總共的列數,這里實際意思應該是半徑的所有可能取值,加2是為了防止越界,但是說成列數我覺得也沒錯,並且我覺得這樣比較好理解
r+1 是為了把第一列空出來
因為程序后面要比較前一行與前一列的數據, 這樣省的越界
因此空出首行和首列*/
}
}
// stage 2. find local maximums
// 執行步驟2,找到局部極大值,即非極大值抑制
// 霍夫空間,局部最大點,采用四領域判斷,比較。(也可以使8鄰域或者更大的方式),如果不判斷局部最大值,同時選用次大值與最大值,就可能會是兩個相鄰的直線,但實際是一條直線。
// 選用最大值,也是去除離散的近似計算帶來的誤差,或合並近似曲線。
for( r = 0 ; r < numrho; r++ )
for( n = 0; n < numangle; n++ )
{
//得到當前值在累加器數組的位置
int base = (n+1)*(numrho+2) + r + 1;
//得到計數值,並以它為基准,看看它是不是局部極大值
if( accum[base] > threshold &&
accum[base] > accum[base - 1] && accum[base] >= accum[base+1] &&
accum[base] > accum[base - numrho - 2] && accum[base] >= accum[base + numrho + 2)
//把極大值位置存入排序數組內——sort_buf
sort_buf[total++] = base;
}
//stage 3. sort the detected lines by accumulator value
//執行步驟3,對存儲在sort_buf數組內的累加器的數據按由大到小的順序進行排序
icvHoughSortDescent32s( sort_buf, total, accum );
/*OpenCV中自帶了一個排序函數,名稱為:
void icvHoughSortDescent32s(int *sequence , int sum , int*data),參數解釋:
第三個參數:數組的首地址
第二個參數:要排序的數據總數目
第一個參數:此數組存放data中要參與排序的數據的序號
而且這個排序算法改變的只是sequence[]數組中的元素,源數據data[]未發生絲毫改變。
*/
// stage 4. store the first min(total, linesMax ) lines to the output buffer,輸出直線
lineMax = MIN(lineMax, total); //linesMax是輸入參數,表示最多輸出幾條直線
//事先定義一個尺度
scale = 1./(numrho+2);
for(i=0; i<linesMax; i++) // 依據霍夫空間分辨率,計算直線的實際r,theta參數
{
//CvLinePolar 直線的數據結構
//CvLinePolar結構在該文件的前面被定義
CvLinePolar line;
//idx為極大值在累加器數組的位置
int idx = sort_buf[i]; //找到索引(下標)
//分離出該極大值在霍夫空間中的位置
//因為n是從0開始的,而之前為了防止越界,所以將所有的n+1了,因此下面要-1,同理r
int n = cvFloor(idx*scale) - 1; //向下取整
int r = idx - (n+1)*(numrho+2) - 1;
//最終得到極大值所對應的角度和距離
line.rho = (r - (numrho - 1)*0.5f)*rho; //因為之前統一將r+= (numrho-1)/2, 因此需要還原以獲得真實的rho
line.angle = n * theta;
//存儲到序列內
cvSeqPush( lines, &line ); //用序列存放多條直線
}
}
5.2 HoughLinesP源碼分析
這個代碼與之前HoughLines風格完全不同,個人感覺沒有之前HoughLines的優美,同時小優化也並不是特別注意,不過實現算法思想的大體思路還是值得我這個初學者借鑒的,但是里面那個shitf操作沒看懂,不是很理解,如果有同學會的話,希望解釋一下
static void
icvHoughLinesProbabilistic( CvMat* image,
float rho, float theta, int threshold,
int lineLength, int lineGap,
CvSeq *lines, int linesMax )
{
//accum為累加器矩陣,mask為掩碼矩陣
cv::Mat accum, mask;
cv::vector<float> trigtab; //用於存儲事先計算好的正弦和余弦值
//開辟一段內存空間
cv::MemStorage storage(cvCreateMemStorage(0));
//用於存儲特征點坐標,即邊緣像素的位置
CvSeq* seq;
CvSeqWriter writer;
int width, height; //圖像的寬和高
int numangle, numrho; //角度和距離的離散數量
float ang;
int r, n, count;
CvPoint pt;
float irho = 1 / rho; //距離分辨率的倒數
CvRNG rng = cvRNG(-1); //隨機數
const float* ttab; //向量trigtab的地址指針
uchar* mdata0; //矩陣mask的地址指針
//確保輸入圖像的正確性
CV_Assert( CV_IS_MAT(image) && CV_MAT_TYPE(image->type) == CV_8UC1 );
width = image->cols; //提取出輸入圖像的寬
height = image->rows; //提取出輸入圖像的高
//由角度和距離分辨率,得到角度和距離的離散數量
numangle = cvRound(CV_PI / theta);
numrho = cvRound(((width + height) * 2 + 1) / rho);
//創建累加器矩陣,即霍夫空間
accum.create( numangle, numrho, CV_32SC1 );
//創建掩碼矩陣,大小與輸入圖像相同
mask.create( height, width, CV_8UC1 );
//定義trigtab的大小,因為要存儲正弦和余弦值,所以長度為角度離散數的2倍
trigtab.resize(numangle*2);
//累加器矩陣清零
accum = cv::Scalar(0);
//避免重復計算,事先計算好所需的所有正弦和余弦值
for( ang = 0, n = 0; n < numangle; ang += theta, n++ )
{
trigtab[n*2] = (float)(cos(ang) * irho);
trigtab[n*2+1] = (float)(sin(ang) * irho);
}
//賦值首地址
ttab = &trigtab[0];
mdata0 = mask.data;
//開始寫入序列
cvStartWriteSeq( CV_32SC2, sizeof(CvSeq), sizeof(CvPoint), storage, &writer );
// stage 1. collect non-zero image points
//收集圖像中的所有非零點,因為輸入圖像是邊緣圖像,所以非零點就是邊緣點
for( pt.y = 0, count = 0; pt.y < height; pt.y++ )
{
//提取出輸入圖像和掩碼矩陣的每行地址指針
const uchar* data = image->data.ptr + pt.y*image->step; // step是每一行的字節大小 此行代碼就轉到當前遍歷的這一行
uchar* mdata = mdata0 + pt.y*width;
for( pt.x = 0; pt.x < width; pt.x++ )
{
if( data[pt.x] ) //是邊緣點
{
mdata[pt.x] = (uchar)1; //掩碼的相應位置置1
CV_WRITE_SEQ_ELEM( pt, writer ); 把該坐標位置寫入序列
}
else //不是邊緣點
mdata[pt.x] = 0; //掩碼的相應位置清0
}
}
//終止寫序列,seq為所有邊緣點坐標位置的序列
seq = cvEndWriteSeq( &writer );
count = seq->total; //得到邊緣點的數量
// stage 2. process all the points in random order
//隨機處理所有的邊緣點
for( ; count > 0; count-- )
{
// choose random point out of the remaining ones
//步驟1,在剩下的邊緣點中隨機選擇一個點,idx為不大於count的隨機數
int idx = cvRandInt(&rng) % count;
//max_val為累加器的最大值,max_n為最大值所對應的角度
int max_val = threshold-1, max_n = 0;
//由隨機數idx在序列中提取出所對應的坐標點
CvPoint* point = (CvPoint*)cvGetSeqElem( seq, idx );
//定義直線的兩個端點
CvPoint line_end[2] = {{0,0}, {0,0}};
float a, b;
//累加器的地址指針,也就是霍夫空間的地址指針
int* adata = (int*)accum.data;
int i, j, k, x0, y0, dx0, dy0, xflag;
int good_line;
const int shift = 16; //
//提取出坐標點的橫、縱坐標
i = point->y;
j = point->x;
// "remove" it by overriding it with the last element
//用序列中的最后一個元素覆蓋掉剛才提取出來的隨機坐標點
*point = *(CvPoint*)cvGetSeqElem( seq, count-1 );
// check if it has been excluded already (i.e. belongs to some other line)
//檢測這個坐標點是否已經計算過,也就是它已經屬於其他直線
//因為計算過的坐標點會在掩碼矩陣mask的相對應位置清零
if( !mdata0[i*width + j] ) //該坐標點被處理過
continue; //不做任何處理,繼續主循環
// update accumulator, find the most probable line
//步驟2,更新累加器矩陣,找到最有可能的直線
for( n = 0; n < numangle; n++, adata += numrho )
{
//由角度計算距離
r = cvRound( j * ttab[n*2] + i * ttab[n*2+1] );
r += (numrho - 1) / 2; //防止r為負數
//在累加器矩陣的相應位置上數值加1,並賦值給val
int val = ++adata[r];
//更新最大值,並得到它的角度
if( max_val < val )
{
max_val = val;
max_n = n;
}
}
// if it is too "weak" candidate, continue with another point
//步驟3,如果上面得到的最大值小於閾值,則放棄該點,繼續下一個點的計算
if( max_val < threshold )
continue;
// from the current point walk in each direction
// along the found line and extract the line segment
//步驟4,從當前點出發,沿着它所在直線的方向前進,直到達到端點為止
a = -ttab[max_n*2+1]; //a=-sinθ
b = ttab[max_n*2]; //b=cosθ
//當前點的橫、縱坐標值
x0 = j;
y0 = i;
//確定當前點所在直線的角度是在45度~135度之間,還是在0~45或135度~180度之間
if( fabs(a) > fabs(b) ) //在45度~135度之間
{
xflag = 1; //置標識位,標識直線的粗略方向
//確定橫、縱坐標的位移量
dx0 = a > 0 ? 1 : -1;
dy0 = cvRound( b*(1 << shift)/fabs(a) );
//確定縱坐標
y0 = (y0 << shift) + (1 << (shift-1));
}
else //在0~45或135度~180度之間
{
xflag = 0; //清標識位
//確定橫、縱坐標的位移量
dy0 = b > 0 ? 1 : -1;
dx0 = cvRound( a*(1 << shift)/fabs(b) );
//確定橫坐標
x0 = (x0 << shift) + (1 << (shift-1));
}
//搜索直線的兩個端點
for( k = 0; k < 2; k++ )
{
//gap表示兩條直線的間隙,x和y為搜索位置,dx和dy為位移量
int gap = 0, x = x0, y = y0, dx = dx0, dy = dy0;
//搜索第二個端點的時候,反方向位移
if( k > 0 )
dx = -dx, dy = -dy;
// walk along the line using fixed-point arithmetics,
// stop at the image border or in case of too big gap
//沿着直線的方向位移,直到到達圖像的邊界或大的間隙為止
for( ;; x += dx, y += dy )
{
uchar* mdata;
int i1, j1;
//確定新的位移后的坐標位置
if( xflag )
{
j1 = x;
i1 = y >> shift;
}
else
{
j1 = x >> shift;
i1 = y;
}
//如果到達了圖像的邊界,停止位移,退出循環
if( j1 < 0 || j1 >= width || i1 < 0 || i1 >= height )
break;
//定位位移后掩碼矩陣位置
mdata = mdata0 + i1*width + j1;
// for each non-zero point:
// update line end,
// clear the mask element
// reset the gap
//該掩碼不為0,說明該點可能是在直線上
if( *mdata )
{
gap = 0; //設置間隙為0
//更新直線的端點位置
line_end[k].y = i1;
line_end[k].x = j1;
}
//掩碼為0,說明不是直線,但仍繼續位移,直到間隙大於所設置的閾值為止
else if( ++gap > lineGap ) //間隙加1
break;
}
}
//步驟5,由檢測到的直線的兩個端點粗略計算直線的長度
//當直線長度大於所設置的閾值時,good_line為1,否則為0
good_line = abs(line_end[1].x - line_end[0].x) >= lineLength ||
abs(line_end[1].y - line_end[0].y) >= lineLength;
//再次搜索端點,目的是更新累加器矩陣和更新掩碼矩陣,以備下一次循環使用
for( k = 0; k < 2; k++ )
{
int x = x0, y = y0, dx = dx0, dy = dy0;
if( k > 0 )
dx = -dx, dy = -dy;
// walk along the line using fixed-point arithmetics,
// stop at the image border or in case of too big gap
for( ;; x += dx, y += dy )
{
uchar* mdata;
int i1, j1;
if( xflag )
{
j1 = x;
i1 = y >> shift;
}
else
{
j1 = x >> shift;
i1 = y;
}
mdata = mdata0 + i1*width + j1;
// for each non-zero point:
// update line end,
// clear the mask element
// reset the gap
if( *mdata )
{
//if語句的作用是清除那些已經判定是好的直線上的點對應的累加器的值,避免再次利用這些累加值
if( good_line ) //在第一次搜索中已經確定是好的直線
{
//得到累加器矩陣地址指針
adata = (int*)accum.data;
for( n = 0; n < numangle; n++, adata += numrho )
{
r = cvRound( j1 * ttab[n*2] + i1 * ttab[n*2+1] );
r += (numrho - 1) / 2;
adata[r]--; //相應的累加器減1
}
}
//搜索過的位置,不管是好的直線,還是壞的直線,掩碼相應位置都清0,這樣下次就不會再重復搜索這些位置了,從而達到減小計算邊緣點的目的
*mdata = 0;
}
//如果已經到達了直線的端點,則退出循環
if( i1 == line_end[k].y && j1 == line_end[k].x )
break;
}
}
//如果是好的直線
if( good_line )
{
CvRect lr = { line_end[0].x, line_end[0].y, line_end[1].x, line_end[1].y };
//把兩個端點壓入序列中
cvSeqPush( lines, &lr );
//如果檢測到的直線數量大於閾值,則退出該函數
if( lines->total >= linesMax )
return;
}
}
}
6 霍夫圓變換原理及算法流程
6.1 經典霍夫圓變換
霍夫圓變換和霍夫線變換的原理類似。霍夫線變換是兩個參數(r,θ),霍夫圓需要三個參數,圓心的x,y坐標和圓的半徑,他的方程表達式為\((x-a)^{2} + (y-b)^{2} = c^{2}\),按照標准霍夫線變換思想,在xy平面,三個點在同一個圓上,則它們對應的空間曲面相交於一點(即點(a,b,c))。故我們如果知道一個邊界上的點的數目,足夠多,且這些點與之對應的空間曲面相交於一點。則這些點構成的邊界,就接近一個圓形。上述描述的是標准霍夫圓變換的原理,由於三維空間的計算量大大增大的原因, 標准霍夫圓變化很難被應用到實際中。
具體可以參考下圖:

6.2 霍夫梯度法的原理即算法流程(兩個版本的解釋)
HoughCircles函數實現了圓形檢測,它使用的算法也是改進的霍夫變換——2-1霍夫變換(21HT)。也就是把霍夫變換分為兩個階段,從而減小了霍夫空間的維數。第一階段用於檢測圓心,第二階段從圓心推導出圓半徑。檢測圓心的原理是圓心是它所在圓周所有法線的交匯處,因此只要找到這個交點,即可確定圓心,該方法所用的霍夫空間與圖像空間的性質相同,因此它僅僅是二維空間。檢測圓半徑的方法是從圓心到圓周上的任意一點的距離(即半徑)是相同,只要確定一個閾值,只要相同距離的數量大於該閾值,我們就認為該距離就是該圓心所對應的圓半徑,該方法只需要計算半徑直方圖,不使用霍夫空間。圓心和圓半徑都得到了,那么通過公式1一個圓形就得到了。從上面的分析可以看出,2-1霍夫變換把標准霍夫變換的三維霍夫空間縮小為二維霍夫空間,因此無論在內存的使用上還是在運行效率上,2-1霍夫變換都遠遠優於標准霍夫變換。但該算法有一個不足之處就是由於圓半徑的檢測完全取決於圓心的檢測,因此如果圓心檢測出現偏差,那么圓半徑的檢測肯定也是錯誤的。
version 1:
2-1霍夫變換的具體步驟為:
1)首先對圖像進行邊緣檢測,調用opencv自帶的cvCanny()函數,將圖像二值化,得到邊緣圖像。
2)對邊緣圖像上的每一個非零點。采用cvSobel()函數,計算x方向導數和y方向的導數,從而得到梯度。從邊緣點,沿着梯度和梯度的反方向,對參數指定的min_radius到max_radium的每一個像素,在累加器中被累加。同時記下邊緣圖像中每一個非0點的位置。
3)從(二維)累加器中這些點中選擇候選中心。這些中心都大於給定的閾值和其相鄰的四個鄰域點的累加值。
4)對於這些候選中心按照累加值降序排序,以便於最支持的像素的中心首次出現。
5)對於每一個中心,考慮到所有的非0像素(非0,梯度不為0),這些像素按照與其中心的距離排序,從最大支持的中心的最小距離算起,選擇非零像素最支持的一條半徑。
6)如果一個中心受到邊緣圖像非0像素的充分支持,並且到前期被選擇的中心有足夠的距離。則將圓心和半徑壓入到序列中,得以保留。
version 2:
第一階段:檢測圓心
1.1、對輸入圖像邊緣檢測;
1.2、計算圖形的梯度,並確定圓周線,其中圓周的梯度就是它的法線;
1.3、在二維霍夫空間內,繪出所有圖形的梯度直線,某坐標點上累加和的值越大,說明在該點上直線相交的次數越多,也就是越有可能是圓心;(備注:這只是直觀的想法,實際源碼並沒有划線)
1.4、在霍夫空間的4鄰域內進行非最大值抑制;
1.5、設定一個閾值,霍夫空間內累加和大於該閾值的點就對應於圓心。
第二階段:檢測圓半徑
2.1、計算某一個圓心到所有圓周線的距離,這些距離中就有該圓心所對應的圓的半徑的值,這些半徑值當然是相等的,並且這些圓半徑的數量要遠遠大於其他距離值相等的數量
2.2、設定兩個閾值,定義為最大半徑和最小半徑,保留距離在這兩個半徑之間的值,這意味着我們檢測的圓不能太大,也不能太小
2.3、對保留下來的距離進行排序
2.4、找到距離相同的那些值,並計算相同值的數量
2.5、設定一個閾值,只有相同值的數量大於該閾值,才認為該值是該圓心對應的圓半徑
2.6、對每一個圓心,完成上面的2.1~2.5步驟,得到所有的圓半徑
7 OpenCV圓變換函數 HoughCircles
C++: void HoughCircles(InputArray image,OutputArray circles, int method, double dp,
double minDist, double param1=100,double param2=100, int minRadius=0, int maxRadius=0 )
第一個參數,InputArray類型的image,輸入圖像,即源圖像,需為8位的灰度單通道圖像。
第二個參數,InputArray類型的circles,經過調用HoughCircles函數后此參數存儲了檢測到的圓的輸出矢量,每個矢量由包含了3個元素的浮點矢量(x, y, radius)表示。
第三個參數,int類型的method,即使用的檢測方法,目前OpenCV中就霍夫梯度法一種可以使用,它的標識符為CV_HOUGH_GRADIENT,在此參數處填這個標識符即可。
第四個參數,double類型的dp,用來檢測圓心的累加器圖像的分辨率於輸入圖像之比的倒數,且此參數允許創建一個比輸入圖像分辨率低的累加器。上述文字不好理解的話,來看例子吧。例如,如果dp= 1時,累加器和輸入圖像具有相同的分辨率。如果dp=2,累加器便有輸入圖像一半那么大的寬度和高度。
第五個參數,double類型的minDist,為霍夫變換檢測到的圓的圓心之間的最小距離,即讓我們的算法能明顯區分的兩個不同圓之間的最小距離。這個參數如果太小的話,多個相鄰的圓可能被錯誤地檢測成了一個重合的圓。反之,這個參數設置太大的話,某些圓就不能被檢測出來了。
第六個參數,double類型的param1,有默認值100。它是第三個參數method設置的檢測方法的對應的參數。對當前唯一的方法霍夫梯度法CV_HOUGH_GRADIENT,它表示傳遞給canny邊緣檢測算子的高閾值,而低閾值為高閾值的一半。
第七個參數,double類型的param2,也有默認值100。它是第三個參數method設置的檢測方法的對應的參數。對當前唯一的方法霍夫梯度法CV_HOUGH_GRADIENT,它表示在檢測階段圓心的累加器閾值。它越小的話,就可以檢測到更多根本不存在的圓,而它越大的話,能通過檢測的圓就更加接近完美的圓形了。
第八個參數,int類型的minRadius,有默認值0,表示圓半徑的最小值。
第九個參數,int類型的maxRadius,也有默認值0,表示圓半徑的最大值。
8 源碼分析
有兩個版本的注釋,一樣的,結合來看
其中幾個點:
霍夫空間是用於統計坐標點,分辨率沒有必要與原圖像一致,所以用dp來調整霍夫空間的大小,從而提高運算速度。而ONE的作用是為了減小運算過程中的累積誤差,提高精度,如:1/3=0.333333,如果保留小數點后5位,則為0.33333,但如果向左位移3位,則為333.33333,這個數的精度要比前一個高,只要我們把所有的數都向左位移3位,最終的結果再向右位移3位,最后的數值精度會提高不少的。基本思想就是這個。
8.1 version1:論文中的
/****************************************************************************************\
* Circle Detection *
\****************************************************************************************/
/*------------------------------------霍夫梯度法------------------------------------------*/
static void
icvHoughCirclesGradient( CvMat* img, float dp, float min_dist,
int min_radius, int max_radius,
int canny_threshold, int acc_threshold,
CvSeq* circles, int circles_max )
{
const int SHIFT = 10, ONE = 1 << SHIFT, R_THRESH = 30; //One=1024,1左移10位2*10,R_THRESH是起始值,賦給max_count,后續會被覆蓋。
cv::Ptr<CvMat> dx, dy; //Ptr是智能指針模板,將CvMat對象封裝成指針
cv::Ptr<CvMat> edges, accum, dist_buf;//edges邊緣二值圖像,accum為累加器圖像,dist_buf存放候選圓心到滿足條件的邊緣點的半徑
std::vector<int> sort_buf;//用來進行排序的中間對象。在adata累加器排序中,其存放的是offset即偏移位置,int型。在ddata距離排序中,其存儲的和下標是一樣的值。
cv::Ptr<CvMemStorage> storage;//內存存儲器。創建的序列用來向其申請內存空間。
int x, y, i, j, k, center_count, nz_count;//center_count為圓心數,nz_count為非零數
float min_radius2 = (float)min_radius*min_radius;//最小半徑的平方
float max_radius2 = (float)max_radius*max_radius;//最大半徑的平方
int rows, cols, arows,acols;//rows,cols邊緣圖像的行數和列數,arows,acols是累加器圖像的行數和列數
int astep, *adata;//adata指向累加器數據域的首地址,用位置作為下標,astep為累加器每行的大小,以字節為單位
float* ddata;//ddata即dist_data,距離數據
CvSeq *nz, *centers;//nz為非0,即邊界,centers為存放的候選中心的位置。
float idp, dr;//idp即inv_dp,dp的倒數
CvSeqReader reader;//順序讀取序列中的每個值
edges = cvCreateMat( img->rows, img->cols, CV_8UC1 );//邊緣圖像
cvCanny( img, edges, MAX(canny_threshold/2,1), canny_threshold, 3 );//調用canny,變為二值圖像,0和非0即0和255
dx = cvCreateMat( img->rows, img->cols, CV_16SC1 );//16位單通道圖像,用來存儲二值邊緣圖像的x方向的一階導數
dy = cvCreateMat( img->rows, img->cols, CV_16SC1 );//y方向的
cvSobel( img, dx, 1, 0, 3 );//計算x方向的一階導數
cvSobel( img, dy, 0, 1, 3 );//計算y方向的一階導數
if( dp < 1.f )//控制dp不能比1小
dp = 1.f;
idp = 1.f/dp;
accum = cvCreateMat( cvCeil(img->rows*idp)+2, cvCeil(img->cols*idp)+2, CV_32SC1 );//cvCeil返回不小於參數的最小整數。32為單通道
cvZero(accum);//初始化累加器為0
storage = cvCreateMemStorage();//創建內存存儲器,使用默認參數0.默認大小為64KB
nz = cvCreateSeq( CV_32SC2, sizeof(CvSeq), sizeof(CvPoint), storage );//創建序列,用來存放非0點
centers = cvCreateSeq( CV_32SC1, sizeof(CvSeq), sizeof(int), storage );//用來存放圓心
rows = img->rows;
cols = img->cols;
arows = accum->rows - 2;
acols = accum->cols - 2;
adata = accum->data.i;//cvMat對象的union對象的i成員成員
//step是矩陣中行的長度,單位為字節。我們使用到的矩陣是accum它的深度是CV_32SC1即32位的int 型。
//如果我們知道一個指針如int* p;指向數組中的一個元素, 則可以通過p+accum->step/adata[0]來使指針移動到p指針所指元素的,正對的下一行元素
astep = accum->step/sizeof(adata[0]);
for( y = 0; y < rows; y++ )
{
const uchar* edges_row = edges->data.ptr + y*edges->step; //邊界存儲的矩陣的每一行的指向行首的指針。
const short* dx_row = (const short*)(dx->data.ptr + y*dx->step);//存儲 x方向sobel一階導數的矩陣的每一行的指向第一個元素的指針
const short* dy_row = (const short*)(dy->data.ptr + y*dy->step);//y
//遍歷邊緣的二值圖像和偏導數的圖像
for( x = 0; x < cols; x++ )
{
float vx, vy;
int sx, sy, x0, y0, x1, y1, r, k;
CvPoint pt;
vx = dx_row[x];//訪問每一行的元素
vy = dy_row[x];
if( !edges_row[x] || (vx == 0 && vy == 0) )//如果在邊緣圖像(存儲邊緣的二值圖像)某一點如A(x0,y0)==0則對一下點進行操作。vx和vy同時為0,則下一個
continue;
float mag = sqrt(vx*vx+vy*vy);//求梯度圖像
assert( mag >= 1 );//如果mag為0,說明沒有邊緣點,則stop。這里用了assert宏定義
sx = cvRound((vx*idp)*ONE/mag);// vx為該點的水平梯度(梯度幅值已經歸一化);ONE為為了用整數運算代替浮點數引入的一個因子,為2^10
sy = cvRound((vy*idp)*ONE/mag);
x0 = cvRound((x*idp)*ONE);
y0 = cvRound((y*idp)*ONE);
for( k = 0; k < 2; k++ )//k=0在梯度方向,k=1在梯度反方向對累加器累加。這里之所以要反向,因為對於一個圓上一個點,從這個點沿着斜率的方向的,最小半徑到最大半徑。在圓的另一邊與其相對應的點,有對應的效果。
{
x1 = x0 + min_radius * sx;
y1 = y0 + min_radius * sy;
for( r = min_radius; r <= max_radius; x1 += sx, y1 += sy, r++ )//x1=x1+sx即,x1=x0+min_radius*sx+sx=x0+(min_radius+1)*sx求得下一個點。sx為斜率
{
int x2 = x1 >> SHIFT, y2 = y1 >> SHIFT; //變回真實的坐標
if( (unsigned)x2 >= (unsigned)acols || //如果x2大於累加器的行
(unsigned)y2 >= (unsigned)arows )
break;
adata[y2*astep + x2]++;//由於c語言是按行存儲的。即等價於對accum數組進行了操作。
}
sx = -sx; sy = -sy;
}
pt.x = x; pt.y = y;
cvSeqPush( nz, &pt );//把非零邊緣並且梯度不為0的點壓入到堆棧
}
}
nz_count = nz->total;
if( !nz_count )//如果nz_count==0則返回
return;
for( y = 1; y < arows - 1; y++ ) //這里是從1到arows-1,因為如果是圓的話,那么圓的半徑至少為1,即圓心至少在內層里面
{
for( x = 1; x < acols - 1; x++ )
{
int base = y*(acols+2) + x;//計算位置,在accum圖像中
if( adata[base] > acc_threshold &&
adata[base] > adata[base-1] && adata[base] > adata[base+1] &&
adata[base] > adata[base-acols-2] && adata[base] > adata[base+acols+2] )
cvSeqPush(centers, &base);//候選中心點位置壓入到堆棧。其候選中心點累加數大於閾值,其大於四個鄰域
}
}
center_count = centers->total;
if( !center_count ) //如果沒有符合條件的圓心,則返回到函數。
return;
sort_buf.resize( MAX(center_count,nz_count) );//重新分配容器的大小,取候選圓心的個數和非零邊界的個數的最大值。因為后面兩個均用到排序。
cvCvtSeqToArray( centers, &sort_buf[0] ); //把序列轉換成數組,即把序列centers中的數據放入到sort_buf的容器中。
icvHoughSortDescent32s( &sort_buf[0], center_count, adata );//快速排序,根據sort_buf中的值作為下標,依照adata中對應的值進行排序,將累加值大的下標排到前面
cvClearSeq( centers );//清空序列
cvSeqPushMulti( centers, &sort_buf[0], center_count );//重新將中心的下標存入centers
dist_buf = cvCreateMat( 1, nz_count, CV_32FC1 );//創建一個32為浮點型的一個行向量
ddata = dist_buf->data.fl;//使ddata執行這個行向量的首地址
dr = dp;
min_dist = MAX( min_dist, dp );//如果輸入的最小距離小於dp,則設在為dp
min_dist *= min_dist;
for( i = 0; i < centers->total; i++ ) //對於每一個中心點
{
int ofs = *(int*)cvGetSeqElem( centers, i );//獲取排序的中心位置,adata值最大的元素,排在首位 ,offset偏移位置
y = ofs/(acols+2) - 1;//這里因為edge圖像比accum圖像小兩個邊。
x = ofs - (y+1)*(acols+2) - 1;//求得y坐標
float cx = (float)(x*dp), cy = (float)(y*dp);
float start_dist, dist_sum;
float r_best = 0, c[3];
int max_count = R_THRESH;
for( j = 0; j < circles->total; j++ )//中存儲已經找到的圓;若當前候選圓心與其中的一個圓心距離<min_dist,則舍棄該候選圓心
{
float* c = (float*)cvGetSeqElem( circles, j );//獲取序列中的元素。
if( (c[0] - cx)*(c[0] - cx) + (c[1] - cy)*(c[1] - cy) < min_dist )
break;
}
if( j < circles->total )//當前候選圓心與任意已檢測的圓心距離不小於min_dist時,才有j==circles->total
continue;
cvStartReadSeq( nz, &reader );
for( j = k = 0; j < nz_count; j++ )//每個候選圓心,對於所有的點
{
CvPoint pt;
float _dx, _dy, _r2;
CV_READ_SEQ_ELEM( pt, reader );
_dx = cx - pt.x; _dy = cy - pt.y; //中心點到邊界的距離
_r2 = _dx*_dx + _dy*_dy;
if(min_radius2 <= _r2 && _r2 <= max_radius2 )
{
ddata[k] = _r2; //把滿足的半徑的平方存起來
sort_buf[k] = k;//sort_buf同上,但是這里的sort_buf的下標值和元素值是相同的,重新利用
k++;//k和j是兩個游標
}
}
int nz_count1 = k, start_idx = nz_count1 - 1;
if( nz_count1 == 0 )
continue; //如果一個候選中心到(非零邊界且梯度>0)確定的點的距離中,沒有滿足條件的,則從下一個中心點開始。
dist_buf->cols = nz_count1;//用來存放真是的滿足條件的非零元素(三個約束:非零點,梯度不為0,到圓心的距離在min_radius和max_radius中間)
cvPow( dist_buf, dist_buf, 0.5 );//對dist_buf中的元素開根號.求得半徑
icvHoughSortDescent32s( &sort_buf[0], nz_count1, (int*)ddata );////對與圓心的距離按降序排列,索引值在sort_buf中
dist_sum = start_dist = ddata[sort_buf[nz_count1-1]];//dist距離,選取半徑最小的作為起始值
//下邊for循環里面是一個算法。它定義了兩個游標(指針)start_idx和j,j是外層循環的控制變量。而start_idx為控制當兩個相鄰的數組ddata的數據發生變化時,即d-start_dist>dr時,的步進。
for( j = nz_count1 - 2; j >= 0; j-- )//從小到大。選出半徑支持點數最多的半徑
{
float d = ddata[sort_buf[j]];
if( d > max_radius )//如果求得的候選圓點到邊界的距離大於參數max_radius,則停止,因為d是第一個出現的最小的(按照從大到小的順序排列的)
break;
if( d - start_dist > dr )//如果當前的距離減去最小的>dr(==dp)
{
float r_cur = ddata[sort_buf[(j + start_idx)/2]];//當前半徑設為符合該半徑的中值,j和start_idx相當於兩個游標
if( (start_idx - j)*r_best >= max_count*r_cur || //如果數目相等時,它會找半徑較小的那個。這里是判斷支持度的算法
(r_best < FLT_EPSILON && start_idx - j >= max_count) ) //程序這個部分告訴我們,無法找到同心圓,它會被外層最大,支持度最多(支持的點最多)所覆蓋。
{
r_best = r_cur;//如果 符合當前半徑的點數(start_idx - j)/ 當前半徑>= 符合之前最優半徑的點數/之前的最優半徑 || 還沒有最優半徑時,且點數>30時;其實直接把r_best初始值置為1即可省去第二個條件
max_count = start_idx - j;//maxcount變為符合當前半徑的點數,更新max_count值,后續的支持度大的半徑將會覆蓋前面的值。
}
start_dist = d;
start_idx = j;
dist_sum = 0;//如果距離改變較大,則重置distsum為0,再在下面的式子中置為當前值
}
dist_sum += d;//如果距離改變較小,則加上當前值(dist_sum)在這里好像沒有用處。
}
if( max_count > R_THRESH )//符合條件的圓周點大於閾值30,則將圓心、半徑壓棧
{
c[0] = cx;
c[1] = cy;
c[2] = (float)r_best;
cvSeqPush( circles, c );
if( circles->total > circles_max )//circles_max是個很大的數,其值為INT_MAX
return;
}
}
}
CV_IMPL CvSeq*
cvHoughCircles1( CvArr* src_image, void* circle_storage,
int method, double dp, double min_dist,
double param1, double param2,
int min_radius, int max_radius )
{
CvSeq* result = 0;
CvMat stub, *img = (CvMat*)src_image;
CvMat* mat = 0;
CvSeq* circles = 0;
CvSeq circles_header;
CvSeqBlock circles_block;
int circles_max = INT_MAX;
int canny_threshold = cvRound(param1);//cvRound返回和參數最接近的整數值,對一個double類型進行四舍五入
int acc_threshold = cvRound(param2);
img = cvGetMat( img, &stub );//將img轉化成為CvMat對象
if( !CV_IS_MASK_ARR(img)) //圖像必須為8位,單通道圖像
CV_Error( CV_StsBadArg, "The source image must be 8-bit, single-channel" );
if( !circle_storage )
CV_Error( CV_StsNullPtr, "NULL destination" );
if( dp <= 0 || min_dist <= 0 || canny_threshold <= 0 || acc_threshold <= 0 )
CV_Error( CV_StsOutOfRange, "dp, min_dist, canny_threshold and acc_threshold must be all positive numbers" );
min_radius = MAX( min_radius, 0 );
if( max_radius <= 0 )//用來控制當使用默認參數max_radius=0的時候
max_radius = MAX( img->rows, img->cols );
else if( max_radius <= min_radius )
max_radius = min_radius + 2;
if( CV_IS_STORAGE( circle_storage ))//如果傳入的是內存存儲器
{
circles = cvCreateSeq( CV_32FC3, sizeof(CvSeq),
sizeof(float)*3, (CvMemStorage*)circle_storage );
}
else if( CV_IS_MAT( circle_storage ))//如果傳入的參數時數組
{
mat = (CvMat*)circle_storage;
//數組應該是CV_32FC3類型的單列數組。
if( !CV_IS_MAT_CONT( mat->type ) || (mat->rows != 1 && mat->cols != 1) ||//連續,單列,CV_32FC3類型
CV_MAT_TYPE(mat->type) != CV_32FC3 )
CV_Error( CV_StsBadArg,
"The destination matrix should be continuous and have a single row or a single column" );
//將數組轉換為序列
circles = cvMakeSeqHeaderForArray( CV_32FC3, sizeof(CvSeq), sizeof(float)*3,
mat->data.ptr, mat->rows + mat->cols - 1, &circles_header, &circles_block );//由於是單列,故elem_size為mat->rows+mat->cols-1
circles_max = circles->total;
cvClearSeq( circles );//清空序列的內容(如果傳入的有數據的話)
}
else
CV_Error( CV_StsBadArg, "Destination is not CvMemStorage* nor CvMat*" );
switch( method )
{
case CV_HOUGH_GRADIENT:
icvHoughCirclesGradient( img, (float)dp, (float)min_dist,
min_radius, max_radius, canny_threshold,
acc_threshold, circles, circles_max );
break;
default:
CV_Error( CV_StsBadArg, "Unrecognized method id" );
}
if( mat )//給定一個指向圓存儲的數組指針值,則返回0,即NULL
{
if( mat->cols > mat->rows )//因為不知道傳入的是列向量還是行向量。
mat->cols = circles->total;
else
mat->rows = circles->total;
}
else//如果是傳入的是內存存儲器,則返回一個指向一個序列的指針。
result = circles;
return result;
}
8.2 version2:(趙老師)
static void
icvHoughCirclesGradient( CvMat* img, float dp, float min_dist,
int min_radius, int max_radius,
int canny_threshold, int acc_threshold,
CvSeq* circles, int circles_max )
{
//為了提高運算精度,定義一個數值的位移量
const int SHIFT = 10, ONE = 1 << SHIFT;
//定義水平梯度和垂直梯度矩陣的地址指針
cv::Ptr<CvMat> dx, dy;
//定義邊緣圖像、累加器矩陣和半徑距離矩陣的地址指針
cv::Ptr<CvMat> edges, accum, dist_buf;
//定義排序向量
std::vector<int> sort_buf;
cv::Ptr<CvMemStorage> storage;
int x, y, i, j, k, center_count, nz_count;
//事先計算好最小半徑和最大半徑的平方
float min_radius2 = (float)min_radius*min_radius;
float max_radius2 = (float)max_radius*max_radius;
int rows, cols, arows, acols;
int astep, *adata;
float* ddata;
//nz表示圓周序列,centers表示圓心序列
CvSeq *nz, *centers;
float idp, dr;
CvSeqReader reader;
//創建一個邊緣圖像矩陣
edges = cvCreateMat( img->rows, img->cols, CV_8UC1 );
//第一階段
//步驟1.1,用canny邊緣檢測算法得到輸入圖像的邊緣圖像
cvCanny( img, edges, MAX(canny_threshold/2,1), canny_threshold, 3 );
//創建輸入圖像的水平梯度圖像和垂直梯度圖像
dx = cvCreateMat( img->rows, img->cols, CV_16SC1 );
dy = cvCreateMat( img->rows, img->cols, CV_16SC1 );
//步驟1.2,用Sobel算子法計算水平梯度和垂直梯度
cvSobel( img, dx, 1, 0, 3 );
cvSobel( img, dy, 0, 1, 3 );
/確保累加器矩陣的分辨率不小於1
if( dp < 1.f )
dp = 1.f;
//分辨率的倒數
idp = 1.f/dp;
//根據分辨率,創建累加器矩陣
accum = cvCreateMat( cvCeil(img->rows*idp)+2, cvCeil(img->cols*idp)+2, CV_32SC1 );
//初始化累加器為0
cvZero(accum);
//創建兩個序列,
storage = cvCreateMemStorage();
nz = cvCreateSeq( CV_32SC2, sizeof(CvSeq), sizeof(CvPoint), storage );
centers = cvCreateSeq( CV_32SC1, sizeof(CvSeq), sizeof(int), storage );
rows = img->rows; //圖像的高
cols = img->cols; //圖像的寬
arows = accum->rows - 2; //累加器的高
acols = accum->cols - 2; //累加器的寬
adata = accum->data.i; //累加器的地址指針
astep = accum->step/sizeof(adata[0]); /累加器的步長
// Accumulate circle evidence for each edge pixel
//步驟1.3,對邊緣圖像計算累加和
for( y = 0; y < rows; y++ )
{
//提取出邊緣圖像、水平梯度圖像和垂直梯度圖像的每行的首地址
const uchar* edges_row = edges->data.ptr + y*edges->step;
const short* dx_row = (const short*)(dx->data.ptr + y*dx->step);
const short* dy_row = (const short*)(dy->data.ptr + y*dy->step);
for( x = 0; x < cols; x++ )
{
float vx, vy;
int sx, sy, x0, y0, x1, y1, r;
CvPoint pt;
//當前的水平梯度值和垂直梯度值
vx = dx_row[x];
vy = dy_row[x];
//如果當前的像素不是邊緣點,或者水平梯度值和垂直梯度值都為0,則繼續循環。因為如果滿足上面條件,該點一定不是圓周上的點
if( !edges_row[x] || (vx == 0 && vy == 0) )
continue;
//計算當前點的梯度值
float mag = sqrt(vx*vx+vy*vy);
assert( mag >= 1 );
//定義水平和垂直的位移量
sx = cvRound((vx*idp)*ONE/mag);
sy = cvRound((vy*idp)*ONE/mag);
//把當前點的坐標定位到累加器的位置上
x0 = cvRound((x*idp)*ONE);
y0 = cvRound((y*idp)*ONE);
// Step from min_radius to max_radius in both directions of the gradient
//在梯度的兩個方向上進行位移,並對累加器進行投票累計
for(int k1 = 0; k1 < 2; k1++ )
{
//初始一個位移的啟動
//位移量乘以最小半徑,從而保證了所檢測的圓的半徑一定是大於最小半徑
x1 = x0 + min_radius * sx;
y1 = y0 + min_radius * sy;
//在梯度的方向上位移
// r <= max_radius保證了所檢測的圓的半徑一定是小於最大半徑
for( r = min_radius; r <= max_radius; x1 += sx, y1 += sy, r++ )
{
int x2 = x1 >> SHIFT, y2 = y1 >> SHIFT;
//如果位移后的點超過了累加器矩陣的范圍,則退出
if( (unsigned)x2 >= (unsigned)acols ||
(unsigned)y2 >= (unsigned)arows )
break;
//在累加器的相應位置上加1
adata[y2*astep + x2]++;
}
//把位移量設置為反方向
sx = -sx; sy = -sy;
}
//把輸入圖像中的當前點(即圓周上的點)的坐標壓入序列圓周序列nz中
pt.x = x; pt.y = y;
cvSeqPush( nz, &pt );
}
}
//計算圓周點的總數
nz_count = nz->total;
//如果總數為0,說明沒有檢測到圓,則退出該函數
if( !nz_count )
return;
//Find possible circle centers
//步驟1.4和1.5,遍歷整個累加器矩陣,找到可能的圓心
for( y = 1; y < arows - 1; y++ )
{
for( x = 1; x < acols - 1; x++ )
{
int base = y*(acols+2) + x;
//如果當前的值大於閾值,並在4鄰域內它是最大值,則該點被認為是圓心
if( adata[base] > acc_threshold &&
adata[base] > adata[base-1] && adata[base] > adata[base+1] &&
adata[base] > adata[base-acols-2] && adata[base] > adata[base+acols+2] )
//把當前點的地址壓入圓心序列centers中
cvSeqPush(centers, &base);
}
}
//計算圓心的總數
center_count = centers->total;
//如果總數為0,說明沒有檢測到圓,則退出該函數
if( !center_count )
return;
//定義排序向量的大小
sort_buf.resize( MAX(center_count,nz_count) );
//把圓心序列放入排序向量中
cvCvtSeqToArray( centers, &sort_buf[0] );
//對圓心按照由大到小的順序進行排序
//它的原理是經過icvHoughSortDescent32s函數后,以sort_buf中元素作為adata數組下標,adata中的元素降序排列,即adata[sort_buf[0]]是adata所有元素中最大的,adata[sort_buf[center_count-1]]是所有元素中最小的
icvHoughSortDescent32s( &sort_buf[0], center_count, adata );
//清空圓心序列
cvClearSeq( centers );
//把排好序的圓心重新放入圓心序列中
cvSeqPushMulti( centers, &sort_buf[0], center_count );
//創建半徑距離矩陣
dist_buf = cvCreateMat( 1, nz_count, CV_32FC1 );
//定義地址指針
ddata = dist_buf->data.fl;
dr = dp; //定義圓半徑的距離分辨率
//重新定義圓心之間的最小距離
min_dist = MAX( min_dist, dp );
//最小距離的平方
min_dist *= min_dist;
// For each found possible center
// Estimate radius and check support
//按照由大到小的順序遍歷整個圓心序列
for( i = 0; i < centers->total; i++ )
{
//提取出圓心,得到該點在累加器矩陣中的偏移量
int ofs = *(int*)cvGetSeqElem( centers, i );
//得到圓心在累加器中的坐標位置
y = ofs/(acols+2);
x = ofs - (y)*(acols+2);
//Calculate circle's center in pixels
//計算圓心在輸入圖像中的坐標位置
float cx = (float)((x + 0.5f)*dp), cy = (float)(( y + 0.5f )*dp);
float start_dist, dist_sum;
float r_best = 0;
int max_count = 0;
// Check distance with previously detected circles
//判斷當前的圓心與之前確定作為輸出的圓心是否為同一個圓心
for( j = 0; j < circles->total; j++ )
{
//從序列中提取出圓心
float* c = (float*)cvGetSeqElem( circles, j );
//計算當前圓心與提取出的圓心之間的距離,如果兩者距離小於所設的閾值,則認為兩個圓心是同一個圓心,退出循環
if( (c[0] - cx)*(c[0] - cx) + (c[1] - cy)*(c[1] - cy) < min_dist )
break;
}
//如果j < circles->total,說明當前的圓心已被認為與之前確定作為輸出的圓心是同一個圓心,則拋棄該圓心,返回上面的for循環
if( j < circles->total )
continue;
// Estimate best radius
//第二階段
//開始讀取圓周序列nz
cvStartReadSeq( nz, &reader );
for( j = k = 0; j < nz_count; j++ )
{
CvPoint pt;
float _dx, _dy, _r2;
CV_READ_SEQ_ELEM( pt, reader );
_dx = cx - pt.x; _dy = cy - pt.y;
//步驟2.1,計算圓周上的點與當前圓心的距離,即半徑
_r2 = _dx*_dx + _dy*_dy;
//步驟2.2,如果半徑在所設置的最大半徑和最小半徑之間
if(min_radius2 <= _r2 && _r2 <= max_radius2 )
{
//把半徑存入dist_buf內
ddata[k] = _r2;
sort_buf[k] = k;
k++;
}
}
//k表示一共有多少個圓周上的點
int nz_count1 = k, start_idx = nz_count1 - 1;
//nz_count1等於0也就是k等於0,說明當前的圓心沒有所對應的圓,意味着當前圓心不是真正的圓心,所以拋棄該圓心,返回上面的for循環
if( nz_count1 == 0 )
continue;
dist_buf->cols = nz_count1; //得到圓周上點的個數
cvPow( dist_buf, dist_buf, 0.5 ); //求平方根,得到真正的圓半徑
//步驟2.3,對圓半徑進行排序
icvHoughSortDescent32s( &sort_buf[0], nz_count1, (int*)ddata );
dist_sum = start_dist = ddata[sort_buf[nz_count1-1]];
//步驟2.4
for( j = nz_count1 - 2; j >= 0; j-- )
{
float d = ddata[sort_buf[j]];
if( d > max_radius )
break;
//d表示當前半徑值,start_dist表示上一次通過下面if語句更新后的半徑值,dr表示半徑距離分辨率,如果這兩個半徑距離之差大於距離分辨率,說明這兩個半徑一定不屬於同一個圓,而兩次滿足if語句條件之間的那些半徑值可以認為是相等的,即是屬於同一個圓
if( d - start_dist > dr )
{
//start_idx表示上一次進入if語句時更新的半徑距離排序的序號
// start_idx – j表示當前得到的相同半徑距離的數量
//(j + start_idx)/2表示j和start_idx中間的數
//取中間的數所對應的半徑值作為當前半徑值r_cur,也就是取那些半徑值相同的值
float r_cur = ddata[sort_buf[(j + start_idx)/2]];
//如果當前得到的半徑相同的數量大於最大值max_count,則進入if語句
if( (start_idx - j)*r_best >= max_count*r_cur ||
(r_best < FLT_EPSILON && start_idx - j >= max_count) )
{
r_best = r_cur; //把當前半徑值作為最佳半徑值
max_count = start_idx - j; //更新最大值
}
//更新半徑距離和序號
start_dist = d;
start_idx = j;
dist_sum = 0;
}
dist_sum += d;
}
// Check if the circle has enough support
//步驟2.5,最終確定輸出
//如果相同半徑的數量大於所設閾值
if( max_count > acc_threshold )
{
float c[3];
c[0] = cx; //圓心的橫坐標
c[1] = cy; //圓心的縱坐標
c[2] = (float)r_best; //所對應的圓的半徑
cvSeqPush( circles, c ); //壓入序列circles內
//如果得到的圓大於閾值,則退出該函數
if( circles->total > circles_max )
return;
}
}
}
9 參考文章
https://blog.csdn.net/qq_37059483/article/details/77916655
https://blog.csdn.net/m0_37264397/article/details/72729423
https://blog.csdn.net/zhaocj/article/details/50454847
https://blog.csdn.net/shanchuan2012/article/details/74010561
http://www.cnblogs.com/AndyJee/p/3805594.html
https://blog.csdn.net/cy513/article/details/4269340
https://blog.csdn.net/poem_qianmo/article/details/26977557
http://homepages.inf.ed.ac.uk/rbf/HIPR2/hough.htm
https://blog.csdn.net/m0_37264397/article/details/72729423
https://www.cnblogs.com/AndyJee/p/3805594.html
---恢復內容結束---
@1 簡述
霍夫變換是一個經典的特征提取技術,本文主要說的是霍夫線/圓變換,即從圖像中獲取直線與圓,同時需要對圖像進行二值化操作,效果如下。

霍夫變換目的通過投票程序在特定類型的形狀內找到對象的不完美示例,這個投票程序是在一個參數空間中進行的,在這個參數空間中,候選對象被當作所謂的累加器空間中的局部最大值來獲得,所述累加器空間由用於計算霍夫變換的算法明確的構建,霍夫變換不僅能夠識別出圖像中有無需要檢測的圖形,而且能夠定位到該圖像(包括位置、角度等),有標准霍夫變換,多尺度霍夫變換,統計概率霍夫變換3種較為經典的方法,主要優點是能容忍特征邊界描述中的間隙,並且相對不受圖像噪聲的影響。
2 標准霍夫線變換原理
2.1 霍夫變換直線的方程
直線的方程形式有截距式,斜截式,一般式,點斜式等,但是這些形式都有“奇異”情況,其中一個截距為0,斜率為0, c=0(通常把c除到等式左面,減少一個參數的搜索),另外某些形式的參數空間不是閉的,比如斜截式的斜率k,取值范圍從0到無窮大,給量化搜索帶來了困難。所以在霍夫線變換中采用了如下方程的形式:
其中\(p\)與\(\theta\)都是極坐標下點的極徑與極角(也可以理解\(p\)是原點離直線最近的距離),但並不是極坐標方程,因為還在笛卡爾坐標下表示,兩個參數的意義如下圖:

這個方程的巧妙之處是角度與距離這兩個參數都是有界的,而且沒有奇異的情況,因此可以在參數空間中進行搜索。同時,直線霍夫變換有2個參數通過這一個等式相關聯,所以程序在投票階段只需要遍歷其中一個,通過等式獲取另一個參數從而進行投票與搜索峰值。
2.2 霍夫空間
對於直線來說,可以將圖像的每一條直線與一對參數\((p, \theta)\)相關聯,這個參數\((p, \theta)\)平面有時被稱為霍夫空間,用於二維直線的集合,因此,對於某一指定的點,不同的\((p, \theta)\)代表了不同的直線,我們把\((p, \theta)\)之間的關系通過圖像表示出來——固定一個點(3,4),角度取[0,2\(\pi\)]時,\(r\)的范圍取值情況:

會發現曲線的形狀類似一條正弦曲線,通常\(p\)越大,正弦曲線的振幅越大,反而就會越小。
2.3 檢測直線的方法
可以得到一個結論,給定平面中的單個點,那么通過該點的所有直線的集合對應於(r,θ)平面中的正弦曲線,這對於該點是獨特的。一組兩個或更多點形成一條直線將產生在該線的(r,θ)處交叉的一條或多條正弦曲線。因此,檢測共線點的問題可以轉化為找到並發曲線的問題。
具體的,通過將霍夫參數空間量化為有限間隔或累加器單元來實現變換。隨着算法的運行,每個算法都把\((x_{i}, y_{i})\)轉換為一個離散化的 \((r,θ)\)曲線,並且沿着這條曲線的累加器單元被遞增。累加器陣列中產生的峰值表示圖像中存在相應的直線的有力證據。 換句話說,將每個交點看成一次投票,也就是說\(A(r,θ)=A(r,θ)+1\),所有點都如此進行計算后,可以設置一個閾值,投票大於這個閾值的可以認為是找到的直線。
2.4 一個例子
舉一個具體的例子,來體現霍夫變換的流程同時更深的理解一下該算法(此例子摘取某博客,下文會給出所有參考博客的鏈接)
霍夫變換可用於識別最適合一組給定邊緣點的曲線的參數。該邊緣描述通常從諸如Roberts Cross,Sobel或 Canny邊緣檢測器的特征檢測算子獲得,並且可能是嘈雜的,即其可能包含對應於單個整體特征的多個邊緣片段。此外,由於邊緣檢測器的輸出僅限定圖像中的特征的位置,所以霍夫變換進一步是確定兩個特征是什么(即檢測其具有參數(或其他)的特征描述)以及 它們有多少個存在於圖像中。
為了詳細說明霍夫變換,我們從兩個閉合矩形的簡單圖像開始。

使用 Canny邊緣檢測器可產生一組邊界描述的這個部分,如下圖:

這里我們看到了圖像中的整體邊界,但是這個結果並沒有告訴我們邊界描述中的特征的身份(和數量)。在這種情況下,我們可以使用Hough(線檢測)變換來檢測該圖像的八個單獨的直線段,從而確定對象的真實幾何結構。
如果我們使用這些邊緣/邊界點作為Hough變換的輸入,每一個點通過遍歷不同的\((r, \theta)\)都會在笛卡爾空間中生成一條曲線,當被視為強度圖像時, 累加器陣列看起來像如下所示:

可以利用直方圖均衡技術使得圖像可以讓我們看到包含在低強度像素值中的信息模式,如下圖:

注意,雖然r和θ是概念上的極坐標,但是累加器空間以橫坐標θ和縱坐標r的矩形繪制 。請注意,累加器空間環繞圖像的垂直邊緣,因此實際上只有8個實際峰值。
由梯度圖像中的共線點生成的曲線(r,θ) 在霍夫變換空間中的峰中相交。這些交點表征原始圖像的直線段。有許多方法可用於從累加器陣列中提取這些亮點或局部最大值。例如,一個簡單的方法涉及閾值處理,然后 對累加器陣列圖像中孤立的亮點集群進行一些細化處理。這里我們使用相對閾值來提取(r,θ) ,對應於原始圖像中的每條直線邊緣的點。(換句話說,我們只采用累加器數組中的那些局部最大值,其值等於或大於全局最大值的某個固定百分比。)
從Hough變換空間(即,反霍夫變換)映射回笛卡爾空間產生一組圖像主題的線描述。通過將該圖像疊加在原始的反轉版本上,我們可以確認霍夫變換找到兩個矩形的8個真實邊的結果,並且因此展示出了遮擋場景的基礎幾何形狀。

請注意,在這個簡單的例子中,檢測到的和原始圖像線的對齊精度顯然不完美,這取決於累加器陣列的量化。(還要注意許多圖像邊緣有幾條檢測線,這是因為有幾個附近的霍夫空間峰值具有相似的線參數值,存在控制這種效應的技術,但這里沒有用來說明標准霍夫變換)
還要注意,由霍夫變換產生的線條的長度是無限的。如果我們希望識別產生變換參數的實際線段,則需要進一步的圖像分析以便查看這些無限長線的哪些部分實際上具有點。
為了說明Hough技術對噪聲的魯棒性,Canny邊緣描述已被破壞1%(由椒鹽噪聲引起), 在Hough變換之前,如圖12所示。

霍夫空間如下圖所示:

將這個結果反霍夫變換(相對閾值設置為40%,並將它覆蓋在原來的結果上)

可以通過變換圖像來研究Hough變換對特征邊界中的間隙的敏感性,如下圖:

然后我們再將其變換到霍夫變換空間,如下圖

然后使用40%的相對閾值去對圖像反霍夫變換(同樣也是疊加在原圖上)

在這種情況下,因為累加器空間沒有接收到前面例子中的條目數量,只能找到7個峰值,但這些都是結構相關的線。
3 霍夫線變換的算法流程
3.1 標准霍夫線變換算法流程
- 讀取原始圖像,並轉換成灰度圖,利用閾值分割或者邊緣檢測算子轉換成二值化邊緣圖像
- 初始化霍夫空間, 令所有\(Num(\theta, p) = 0\)
- 對於每一個像素點\((x, y)\),在參數空間中找出所有滿足\(xcos\theta + ysin\theta = p\)的\((\theta, p)\)對,然后令\(Num(\theta, p) = Num(\theta, p) + 1\)
- 統計所有\(Num(\theta, p)\)的大小,取出\(Num(\theta, p) > τ\)的參數(\(τ\)是所設的閾值),從而得到一條直線。
- 將上述流程取出的直線,確定與其相關線段的起始點與終止點(有一些算法,如蝴蝶形狀寬度,峰值走廊之類)
3.2 統計概率霍夫變換算法流程
標准霍夫變換本質上是把圖像映射到它的參數空間上,它需要計算所有的M個邊緣點,這樣它的運算量和所需內存空間都會很大。如果在輸入圖像中只是處理\(m(m<M)\)個邊緣點,則這m個邊緣點的選取是具有一定概率性的,因此該方法被稱為概率霍夫變換(Probabilistic Hough Transform)。該方法還有一個重要的特點就是能夠檢測出線端,即能夠檢測出圖像中直線的兩個端點,確切地定位圖像中的直線。
HoughLinesP函數就是利用概率霍夫變換來檢測直線的。它的一般步驟為:
- 隨機抽取圖像中的一個特征點,即邊緣點,如果該點已經被標定為是某一條直線上的點,則繼續在剩下的邊緣點中隨機抽取一個邊緣點,直到所有邊緣點都抽取完了為止;
- 對該點進行霍夫變換,並進行累加和計算;
- 選取在霍夫空間內值最大的點,如果該點大於閾值的,則進行步驟4,否則回到步驟1;
- 根據霍夫變換得到的最大值,從該點出發,沿着直線的方向位移,從而找到直線的兩個端點;
- 計算直線的長度,如果大於某個閾值,則被認為是好的直線輸出,回到步驟1。
4 OpenCV中的霍夫變換函數
4.1標准霍夫變換HoughLines()函數
void HoughLines(InputArray image,OutputArray lines, double rho,
double theta, int threshold, double srn=0,double stn=0 )
第一個參數,InputArray類型的image,輸入圖像,即源圖像,需為8位的單通道二進制圖像,可以將任意的源圖載入進來后由函數修改成此格式后,再填在這里。
第二個參數,InputArray類型的lines,經過調用HoughLines函數后儲存了霍夫線變換檢測到線條的輸出矢量。每一條線由具有兩個元素的矢量\((p, \theta)\)表示,其中,\(p\)是離坐標原點((0,0)(也就是圖像的左上角)的距離。 \(\theta\)是弧度線條旋轉角度(0~垂直線,π/2~水平線)。
第三個參數,double類型的rho,以像素為單位的距離精度。另一種形容方式是直線搜索時的進步尺寸的單位半徑。PS:Latex中/rho就表示 \(\rho\)。
第四個參數,double類型的theta,以弧度為單位的角度精度。另一種形容方式是直線搜索時的進步尺寸的單位角度。
第五個參數,int類型的threshold,累加平面的閾值參數,即識別某部分為圖中的一條直線時它在累加平面中必須達到的值。大於閾值threshold的線段才可以被檢測通過並返回到結果中。
第六個參數,double類型的srn,有默認值0。對於多尺度的霍夫變換,這是第三個參數進步尺寸rho的除數距離。粗略的累加器進步尺寸直接是第三個參數rho,而精確的累加器進步尺寸為rho/srn。
第七個參數,double類型的stn,有默認值0,對於多尺度霍夫變換,srn表示第四個參數進步尺寸的單位角度theta的除數距離。且如果srn和stn同時為0,就表示使用經典的霍夫變換。否則,這兩個參數應該都為正數。
4.2 統計概率霍夫變換(HoughLinesP)
C++: void HoughLinesP(InputArray image, OutputArray lines,
double rho, double theta, int threshold, double minLineLength=0, double maxLineGap=0 )
第一個參數,InputArray類型的image,輸入圖像,即源圖像,需為8位的單通道二進制圖像,可以將任意的源圖載入進來后由函數修改成此格式后,再填在這里。
第二個參數,InputArray類型的lines,經過調用HoughLinesP函數后后存儲了檢測到的線條的輸出矢量,每一條線由具有四個元素的矢量\((x_1,y_1, x_2, y_2)\)表示,其中,\((x_1, y_1)\)和\((x_2, y_2)\)是每個檢測到的線段的結束點。
第三個參數,double類型的rho,以像素為單位的距離精度。另一種形容方式是直線搜索時的進步尺寸的單位半徑。
第四個參數,double類型的theta,以弧度為單位的角度精度。另一種形容方式是直線搜索時的進步尺寸的單位角度。
第五個參數,int類型的threshold,累加平面的閾值參數,即識別某部分為圖中的一條直線時它在累加平面中必須達到的值。大於閾值threshold的線段才可以被檢測通過並返回到結果中。
第六個參數,double類型的minLineLength,有默認值0,表示最低線段的長度,比這個設定參數短的線段就不能被顯現出來。
第七個參數,double類型的maxLineGap,有默認值0,允許將同一行點與點之間連接起來的最大的距離。
5 源碼分析
此部分參考幾位博主的博客,更改了里面一些我認為不太對的地方以及加上了一些自己的理解還有就是一些沒有解釋的地方
5.1 HoughLines()源碼分析
閱讀源碼之后,發現源碼確實細節方面做得比較好,無論是內存方面,還是效率方面,包括一些小細節,比如避免除法,等等。所以源碼值得借鑒與反復參考,具體解釋如下。
static void icvHoughLinesStandard( const CvMat* img, float rho, float theta, int threshold, CvSeq *lines, int lineMax)
{
cv::AutoBuffer<int> _accum, _sort_buf;
cv::AutoBuffer<float> _tabSin, _tabCos;
const uchar* image;
int step, width, height;
int numangle, numrho;
int total=0;
float ang;
int r, n;
int i, j;
float irho = 1 / rho;
double scale;
//再次確保輸入圖像的正確性
CV_Assert( CV_IS_MAT(img) && CV_MAT_TYPE(img->type) == CV_8UC1);
image = img->data.ptr; //得到圖像的指針
step = img->step; //得到圖像的步長(通道)
width = img->cols; //得到圖像的寬
height = img->rows; //得到圖像的高
//由角度和距離的分辨率得到角度和距離的數量,即霍夫變換后角度和距離的個數
numangle = cvRound(CV_PI / theta); // 霍夫空間,角度方向的大小
numrho = cvRound(((width + height)*2 + 1) / rho); //r的空間范圍, 這里以周長作為rho的上界
/*
allocator類是一個模板類,定義在頭文件memory中,用於內存的分配、釋放、管理,它幫助我們將內存分配和對象構造分離開來。具體地說,allocator類將內存的分配和對象的構造解耦,
分別用allocate和construct兩個函數完成,同樣將內存的釋放和對象的析構銷毀解耦,分別用deallocate和destroy函數完成。
*/
//為累加器數組分配內存空間
//該累加器數組其實就是霍夫空間,它是用一維數組表示二維空間
_accum.allocate((numangle+2) * (numrho + 2));
//為排序數組分配內存空間
_sort_buf.allocate(numangle * numrho);
//為正弦和余弦列表分配內存空間
_tabSin.allocate(numangle);
_tabCos.allocate(numangle);
//分別定義上述內存空間的地址指針
int *accum = _accum, *sort_buf = _sort_buf;
int *tabSin = _tabSin, *tabCos = _tabCos;
//累加器數組清零
memset( accum, 0, sizeof(accum[0]) * (numangle+2) * (numrho+2) );
//為避免重復運算,事先計算好sinθi/ρ和cosθi/ρ
for( ang = 0, n = 0; n < numangle; ang += theta, n++ ) //計算正弦曲線的准備工作,查表
{
tabSin[n] = (float)(sin(ang) * irho);
tabCos[n] = (float)(cos(ang) * irho);
}
//stage 1. fill accumulator
//執行步驟1,逐點進行霍夫空間變換,並把結果放入累加器數組內
for( i = 0 ; i < height; i++)
for( j = 0; j < width; j++)
{
//只對圖像的非零值處理,即只對圖像的邊緣像素進行霍夫變換
if( image[i * step + j] != 0 ) //將每個非零點,轉換為霍夫空間的離散正弦曲線,並統計。
for( n = 0; n < numangle; n++ )
{
//根據公式: ρ = xcosθ + ysinθ
//cvRound()函數:四舍五入
r = cvRound( j * tabCos[n] + i * tabSin[n]);
//numrho是ρ的最大值,或者說最大取值范圍
r += (numrho - 1) / 2; //因為theta是從0到π的,所以cos(theta)是有負的,所以就所有的r += 最大值的一半,讓極徑都>0
//另一方面,這也預防了r小於0,讓本屬於這一行的點跑到了上一行,這樣可能導致同一個位置卻表示了多個不同的“點”
//r表示的是距離,n表示的是角點,在累加器內找到它們所對應的位置(即霍夫空間內的位置),其值加1
accum[(n+1) * (numrho+2)+ r + 1]++;
/*
將1維數組想象成2維數組
n+1是為了第一行空出來
numrho+2 是總共的列數,這里實際意思應該是半徑的所有可能取值,加2是為了防止越界,但是說成列數我覺得也沒錯,並且我覺得這樣比較好理解
r+1 是為了把第一列空出來
因為程序后面要比較前一行與前一列的數據, 這樣省的越界
因此空出首行和首列*/
}
}
// stage 2. find local maximums
// 執行步驟2,找到局部極大值,即非極大值抑制
// 霍夫空間,局部最大點,采用四領域判斷,比較。(也可以使8鄰域或者更大的方式),如果不判斷局部最大值,同時選用次大值與最大值,就可能會是兩個相鄰的直線,但實際是一條直線。
// 選用最大值,也是去除離散的近似計算帶來的誤差,或合並近似曲線。
for( r = 0 ; r < numrho; r++ )
for( n = 0; n < numangle; n++ )
{
//得到當前值在累加器數組的位置
int base = (n+1)*(numrho+2) + r + 1;
//得到計數值,並以它為基准,看看它是不是局部極大值
if( accum[base] > threshold &&
accum[base] > accum[base - 1] && accum[base] >= accum[base+1] &&
accum[base] > accum[base - numrho - 2] && accum[base] >= accum[base + numrho + 2)
//把極大值位置存入排序數組內——sort_buf
sort_buf[total++] = base;
}
//stage 3. sort the detected lines by accumulator value
//執行步驟3,對存儲在sort_buf數組內的累加器的數據按由大到小的順序進行排序
icvHoughSortDescent32s( sort_buf, total, accum );
/*OpenCV中自帶了一個排序函數,名稱為:
void icvHoughSortDescent32s(int *sequence , int sum , int*data),參數解釋:
第三個參數:數組的首地址
第二個參數:要排序的數據總數目
第一個參數:此數組存放data中要參與排序的數據的序號
而且這個排序算法改變的只是sequence[]數組中的元素,源數據data[]未發生絲毫改變。
*/
// stage 4. store the first min(total, linesMax ) lines to the output buffer,輸出直線
lineMax = MIN(lineMax, total); //linesMax是輸入參數,表示最多輸出幾條直線
//事先定義一個尺度
scale = 1./(numrho+2);
for(i=0; i<linesMax; i++) // 依據霍夫空間分辨率,計算直線的實際r,theta參數
{
//CvLinePolar 直線的數據結構
//CvLinePolar結構在該文件的前面被定義
CvLinePolar line;
//idx為極大值在累加器數組的位置
int idx = sort_buf[i]; //找到索引(下標)
//分離出該極大值在霍夫空間中的位置
//因為n是從0開始的,而之前為了防止越界,所以將所有的n+1了,因此下面要-1,同理r
int n = cvFloor(idx*scale) - 1; //向下取整
int r = idx - (n+1)*(numrho+2) - 1;
//最終得到極大值所對應的角度和距離
line.rho = (r - (numrho - 1)*0.5f)*rho; //因為之前統一將r+= (numrho-1)/2, 因此需要還原以獲得真實的rho
line.angle = n * theta;
//存儲到序列內
cvSeqPush( lines, &line ); //用序列存放多條直線
}
}
5.2 HoughLinesP源碼分析
這個代碼與之前HoughLines風格完全不同,個人感覺沒有之前HoughLines的優美,同時小優化也並不是特別注意,不過實現算法思想的大體思路還是值得我這個初學者借鑒的,但是里面那個shitf操作沒看懂,不是很理解,如果有同學會的話,希望解釋一下
static void
icvHoughLinesProbabilistic( CvMat* image,
float rho, float theta, int threshold,
int lineLength, int lineGap,
CvSeq *lines, int linesMax )
{
//accum為累加器矩陣,mask為掩碼矩陣
cv::Mat accum, mask;
cv::vector<float> trigtab; //用於存儲事先計算好的正弦和余弦值
//開辟一段內存空間
cv::MemStorage storage(cvCreateMemStorage(0));
//用於存儲特征點坐標,即邊緣像素的位置
CvSeq* seq;
CvSeqWriter writer;
int width, height; //圖像的寬和高
int numangle, numrho; //角度和距離的離散數量
float ang;
int r, n, count;
CvPoint pt;
float irho = 1 / rho; //距離分辨率的倒數
CvRNG rng = cvRNG(-1); //隨機數
const float* ttab; //向量trigtab的地址指針
uchar* mdata0; //矩陣mask的地址指針
//確保輸入圖像的正確性
CV_Assert( CV_IS_MAT(image) && CV_MAT_TYPE(image->type) == CV_8UC1 );
width = image->cols; //提取出輸入圖像的寬
height = image->rows; //提取出輸入圖像的高
//由角度和距離分辨率,得到角度和距離的離散數量
numangle = cvRound(CV_PI / theta);
numrho = cvRound(((width + height) * 2 + 1) / rho);
//創建累加器矩陣,即霍夫空間
accum.create( numangle, numrho, CV_32SC1 );
//創建掩碼矩陣,大小與輸入圖像相同
mask.create( height, width, CV_8UC1 );
//定義trigtab的大小,因為要存儲正弦和余弦值,所以長度為角度離散數的2倍
trigtab.resize(numangle*2);
//累加器矩陣清零
accum = cv::Scalar(0);
//避免重復計算,事先計算好所需的所有正弦和余弦值
for( ang = 0, n = 0; n < numangle; ang += theta, n++ )
{
trigtab[n*2] = (float)(cos(ang) * irho);
trigtab[n*2+1] = (float)(sin(ang) * irho);
}
//賦值首地址
ttab = &trigtab[0];
mdata0 = mask.data;
//開始寫入序列
cvStartWriteSeq( CV_32SC2, sizeof(CvSeq), sizeof(CvPoint), storage, &writer );
// stage 1. collect non-zero image points
//收集圖像中的所有非零點,因為輸入圖像是邊緣圖像,所以非零點就是邊緣點
for( pt.y = 0, count = 0; pt.y < height; pt.y++ )
{
//提取出輸入圖像和掩碼矩陣的每行地址指針
const uchar* data = image->data.ptr + pt.y*image->step; // step是每一行的字節大小 此行代碼就轉到當前遍歷的這一行
uchar* mdata = mdata0 + pt.y*width;
for( pt.x = 0; pt.x < width; pt.x++ )
{
if( data[pt.x] ) //是邊緣點
{
mdata[pt.x] = (uchar)1; //掩碼的相應位置置1
CV_WRITE_SEQ_ELEM( pt, writer ); 把該坐標位置寫入序列
}
else //不是邊緣點
mdata[pt.x] = 0; //掩碼的相應位置清0
}
}
//終止寫序列,seq為所有邊緣點坐標位置的序列
seq = cvEndWriteSeq( &writer );
count = seq->total; //得到邊緣點的數量
// stage 2. process all the points in random order
//隨機處理所有的邊緣點
for( ; count > 0; count-- )
{
// choose random point out of the remaining ones
//步驟1,在剩下的邊緣點中隨機選擇一個點,idx為不大於count的隨機數
int idx = cvRandInt(&rng) % count;
//max_val為累加器的最大值,max_n為最大值所對應的角度
int max_val = threshold-1, max_n = 0;
//由隨機數idx在序列中提取出所對應的坐標點
CvPoint* point = (CvPoint*)cvGetSeqElem( seq, idx );
//定義直線的兩個端點
CvPoint line_end[2] = {{0,0}, {0,0}};
float a, b;
//累加器的地址指針,也就是霍夫空間的地址指針
int* adata = (int*)accum.data;
int i, j, k, x0, y0, dx0, dy0, xflag;
int good_line;
const int shift = 16; //
//提取出坐標點的橫、縱坐標
i = point->y;
j = point->x;
// "remove" it by overriding it with the last element
//用序列中的最后一個元素覆蓋掉剛才提取出來的隨機坐標點
*point = *(CvPoint*)cvGetSeqElem( seq, count-1 );
// check if it has been excluded already (i.e. belongs to some other line)
//檢測這個坐標點是否已經計算過,也就是它已經屬於其他直線
//因為計算過的坐標點會在掩碼矩陣mask的相對應位置清零
if( !mdata0[i*width + j] ) //該坐標點被處理過
continue; //不做任何處理,繼續主循環
// update accumulator, find the most probable line
//步驟2,更新累加器矩陣,找到最有可能的直線
for( n = 0; n < numangle; n++, adata += numrho )
{
//由角度計算距離
r = cvRound( j * ttab[n*2] + i * ttab[n*2+1] );
r += (numrho - 1) / 2; //防止r為負數
//在累加器矩陣的相應位置上數值加1,並賦值給val
int val = ++adata[r];
//更新最大值,並得到它的角度
if( max_val < val )
{
max_val = val;
max_n = n;
}
}
// if it is too "weak" candidate, continue with another point
//步驟3,如果上面得到的最大值小於閾值,則放棄該點,繼續下一個點的計算
if( max_val < threshold )
continue;
// from the current point walk in each direction
// along the found line and extract the line segment
//步驟4,從當前點出發,沿着它所在直線的方向前進,直到達到端點為止
a = -ttab[max_n*2+1]; //a=-sinθ
b = ttab[max_n*2]; //b=cosθ
//當前點的橫、縱坐標值
x0 = j;
y0 = i;
//確定當前點所在直線的角度是在45度~135度之間,還是在0~45或135度~180度之間
if( fabs(a) > fabs(b) ) //在45度~135度之間
{
xflag = 1; //置標識位,標識直線的粗略方向
//確定橫、縱坐標的位移量
dx0 = a > 0 ? 1 : -1;
dy0 = cvRound( b*(1 << shift)/fabs(a) );
//確定縱坐標
y0 = (y0 << shift) + (1 << (shift-1));
}
else //在0~45或135度~180度之間
{
xflag = 0; //清標識位
//確定橫、縱坐標的位移量
dy0 = b > 0 ? 1 : -1;
dx0 = cvRound( a*(1 << shift)/fabs(b) );
//確定橫坐標
x0 = (x0 << shift) + (1 << (shift-1));
}
//搜索直線的兩個端點
for( k = 0; k < 2; k++ )
{
//gap表示兩條直線的間隙,x和y為搜索位置,dx和dy為位移量
int gap = 0, x = x0, y = y0, dx = dx0, dy = dy0;
//搜索第二個端點的時候,反方向位移
if( k > 0 )
dx = -dx, dy = -dy;
// walk along the line using fixed-point arithmetics,
// stop at the image border or in case of too big gap
//沿着直線的方向位移,直到到達圖像的邊界或大的間隙為止
for( ;; x += dx, y += dy )
{
uchar* mdata;
int i1, j1;
//確定新的位移后的坐標位置
if( xflag )
{
j1 = x;
i1 = y >> shift;
}
else
{
j1 = x >> shift;
i1 = y;
}
//如果到達了圖像的邊界,停止位移,退出循環
if( j1 < 0 || j1 >= width || i1 < 0 || i1 >= height )
break;
//定位位移后掩碼矩陣位置
mdata = mdata0 + i1*width + j1;
// for each non-zero point:
// update line end,
// clear the mask element
// reset the gap
//該掩碼不為0,說明該點可能是在直線上
if( *mdata )
{
gap = 0; //設置間隙為0
//更新直線的端點位置
line_end[k].y = i1;
line_end[k].x = j1;
}
//掩碼為0,說明不是直線,但仍繼續位移,直到間隙大於所設置的閾值為止
else if( ++gap > lineGap ) //間隙加1
break;
}
}
//步驟5,由檢測到的直線的兩個端點粗略計算直線的長度
//當直線長度大於所設置的閾值時,good_line為1,否則為0
good_line = abs(line_end[1].x - line_end[0].x) >= lineLength ||
abs(line_end[1].y - line_end[0].y) >= lineLength;
//再次搜索端點,目的是更新累加器矩陣和更新掩碼矩陣,以備下一次循環使用
for( k = 0; k < 2; k++ )
{
int x = x0, y = y0, dx = dx0, dy = dy0;
if( k > 0 )
dx = -dx, dy = -dy;
// walk along the line using fixed-point arithmetics,
// stop at the image border or in case of too big gap
for( ;; x += dx, y += dy )
{
uchar* mdata;
int i1, j1;
if( xflag )
{
j1 = x;
i1 = y >> shift;
}
else
{
j1 = x >> shift;
i1 = y;
}
mdata = mdata0 + i1*width + j1;
// for each non-zero point:
// update line end,
// clear the mask element
// reset the gap
if( *mdata )
{
//if語句的作用是清除那些已經判定是好的直線上的點對應的累加器的值,避免再次利用這些累加值
if( good_line ) //在第一次搜索中已經確定是好的直線
{
//得到累加器矩陣地址指針
adata = (int*)accum.data;
for( n = 0; n < numangle; n++, adata += numrho )
{
r = cvRound( j1 * ttab[n*2] + i1 * ttab[n*2+1] );
r += (numrho - 1) / 2;
adata[r]--; //相應的累加器減1
}
}
//搜索過的位置,不管是好的直線,還是壞的直線,掩碼相應位置都清0,這樣下次就不會再重復搜索這些位置了,從而達到減小計算邊緣點的目的
*mdata = 0;
}
//如果已經到達了直線的端點,則退出循環
if( i1 == line_end[k].y && j1 == line_end[k].x )
break;
}
}
//如果是好的直線
if( good_line )
{
CvRect lr = { line_end[0].x, line_end[0].y, line_end[1].x, line_end[1].y };
//把兩個端點壓入序列中
cvSeqPush( lines, &lr );
//如果檢測到的直線數量大於閾值,則退出該函數
if( lines->total >= linesMax )
return;
}
}
}
6 霍夫圓變換原理及算法流程
6.1 經典霍夫圓變換
霍夫圓變換和霍夫線變換的原理類似。霍夫線變換是兩個參數(r,θ),霍夫圓需要三個參數,圓心的x,y坐標和圓的半徑,他的方程表達式為\((x-a)^{2} + (y-b)^{2} = c^{2}\),按照標准霍夫線變換思想,在xy平面,三個點在同一個圓上,則它們對應的空間曲面相交於一點(即點(a,b,c))。故我們如果知道一個邊界上的點的數目,足夠多,且這些點與之對應的空間曲面相交於一點。則這些點構成的邊界,就接近一個圓形。上述描述的是標准霍夫圓變換的原理,由於三維空間的計算量大大增大的原因, 標准霍夫圓變化很難被應用到實際中。
具體可以參考下圖:

6.2 霍夫梯度法的原理即算法流程(兩個版本的解釋)
HoughCircles函數實現了圓形檢測,它使用的算法也是改進的霍夫變換——2-1霍夫變換(21HT)。也就是把霍夫變換分為兩個階段,從而減小了霍夫空間的維數。第一階段用於檢測圓心,第二階段從圓心推導出圓半徑。檢測圓心的原理是圓心是它所在圓周所有法線的交匯處,因此只要找到這個交點,即可確定圓心,該方法所用的霍夫空間與圖像空間的性質相同,因此它僅僅是二維空間。檢測圓半徑的方法是從圓心到圓周上的任意一點的距離(即半徑)是相同,只要確定一個閾值,只要相同距離的數量大於該閾值,我們就認為該距離就是該圓心所對應的圓半徑,該方法只需要計算半徑直方圖,不使用霍夫空間。圓心和圓半徑都得到了,那么通過公式1一個圓形就得到了。從上面的分析可以看出,2-1霍夫變換把標准霍夫變換的三維霍夫空間縮小為二維霍夫空間,因此無論在內存的使用上還是在運行效率上,2-1霍夫變換都遠遠優於標准霍夫變換。但該算法有一個不足之處就是由於圓半徑的檢測完全取決於圓心的檢測,因此如果圓心檢測出現偏差,那么圓半徑的檢測肯定也是錯誤的。
version 1:
2-1霍夫變換的具體步驟為:
1)首先對圖像進行邊緣檢測,調用opencv自帶的cvCanny()函數,將圖像二值化,得到邊緣圖像。
2)對邊緣圖像上的每一個非零點。采用cvSobel()函數,計算x方向導數和y方向的導數,從而得到梯度。從邊緣點,沿着梯度和梯度的反方向,對參數指定的min_radius到max_radium的每一個像素,在累加器中被累加。同時記下邊緣圖像中每一個非0點的位置。
3)從(二維)累加器中這些點中選擇候選中心。這些中心都大於給定的閾值和其相鄰的四個鄰域點的累加值。
4)對於這些候選中心按照累加值降序排序,以便於最支持的像素的中心首次出現。
5)對於每一個中心,考慮到所有的非0像素(非0,梯度不為0),這些像素按照與其中心的距離排序,從最大支持的中心的最小距離算起,選擇非零像素最支持的一條半徑。
6)如果一個中心受到邊緣圖像非0像素的充分支持,並且到前期被選擇的中心有足夠的距離。則將圓心和半徑壓入到序列中,得以保留。
version 2:
第一階段:檢測圓心
1.1、對輸入圖像邊緣檢測;
1.2、計算圖形的梯度,並確定圓周線,其中圓周的梯度就是它的法線;
1.3、在二維霍夫空間內,繪出所有圖形的梯度直線,某坐標點上累加和的值越大,說明在該點上直線相交的次數越多,也就是越有可能是圓心;(備注:這只是直觀的想法,實際源碼並沒有划線)
1.4、在霍夫空間的4鄰域內進行非最大值抑制;
1.5、設定一個閾值,霍夫空間內累加和大於該閾值的點就對應於圓心。
第二階段:檢測圓半徑
2.1、計算某一個圓心到所有圓周線的距離,這些距離中就有該圓心所對應的圓的半徑的值,這些半徑值當然是相等的,並且這些圓半徑的數量要遠遠大於其他距離值相等的數量
2.2、設定兩個閾值,定義為最大半徑和最小半徑,保留距離在這兩個半徑之間的值,這意味着我們檢測的圓不能太大,也不能太小
2.3、對保留下來的距離進行排序
2.4、找到距離相同的那些值,並計算相同值的數量
2.5、設定一個閾值,只有相同值的數量大於該閾值,才認為該值是該圓心對應的圓半徑
2.6、對每一個圓心,完成上面的2.1~2.5步驟,得到所有的圓半徑
7 OpenCV圓變換函數 HoughCircles
C++: void HoughCircles(InputArray image,OutputArray circles, int method, double dp,
double minDist, double param1=100,double param2=100, int minRadius=0, int maxRadius=0 )
第一個參數,InputArray類型的image,輸入圖像,即源圖像,需為8位的灰度單通道圖像。
第二個參數,InputArray類型的circles,經過調用HoughCircles函數后此參數存儲了檢測到的圓的輸出矢量,每個矢量由包含了3個元素的浮點矢量(x, y, radius)表示。
第三個參數,int類型的method,即使用的檢測方法,目前OpenCV中就霍夫梯度法一種可以使用,它的標識符為CV_HOUGH_GRADIENT,在此參數處填這個標識符即可。
第四個參數,double類型的dp,用來檢測圓心的累加器圖像的分辨率於輸入圖像之比的倒數,且此參數允許創建一個比輸入圖像分辨率低的累加器。上述文字不好理解的話,來看例子吧。例如,如果dp= 1時,累加器和輸入圖像具有相同的分辨率。如果dp=2,累加器便有輸入圖像一半那么大的寬度和高度。
第五個參數,double類型的minDist,為霍夫變換檢測到的圓的圓心之間的最小距離,即讓我們的算法能明顯區分的兩個不同圓之間的最小距離。這個參數如果太小的話,多個相鄰的圓可能被錯誤地檢測成了一個重合的圓。反之,這個參數設置太大的話,某些圓就不能被檢測出來了。
第六個參數,double類型的param1,有默認值100。它是第三個參數method設置的檢測方法的對應的參數。對當前唯一的方法霍夫梯度法CV_HOUGH_GRADIENT,它表示傳遞給canny邊緣檢測算子的高閾值,而低閾值為高閾值的一半。
第七個參數,double類型的param2,也有默認值100。它是第三個參數method設置的檢測方法的對應的參數。對當前唯一的方法霍夫梯度法CV_HOUGH_GRADIENT,它表示在檢測階段圓心的累加器閾值。它越小的話,就可以檢測到更多根本不存在的圓,而它越大的話,能通過檢測的圓就更加接近完美的圓形了。
第八個參數,int類型的minRadius,有默認值0,表示圓半徑的最小值。
第九個參數,int類型的maxRadius,也有默認值0,表示圓半徑的最大值。
8 源碼分析
有兩個版本的注釋,一樣的,結合來看
其中幾個點:
霍夫空間是用於統計坐標點,分辨率沒有必要與原圖像一致,所以用dp來調整霍夫空間的大小,從而提高運算速度。而ONE的作用是為了減小運算過程中的累積誤差,提高精度,如:1/3=0.333333,如果保留小數點后5位,則為0.33333,但如果向左位移3位,則為333.33333,這個數的精度要比前一個高,只要我們把所有的數都向左位移3位,最終的結果再向右位移3位,最后的數值精度會提高不少的。基本思想就是這個。
8.1 version1:論文中的
/****************************************************************************************\
* Circle Detection *
\****************************************************************************************/
/*------------------------------------霍夫梯度法------------------------------------------*/
static void
icvHoughCirclesGradient( CvMat* img, float dp, float min_dist,
int min_radius, int max_radius,
int canny_threshold, int acc_threshold,
CvSeq* circles, int circles_max )
{
const int SHIFT = 10, ONE = 1 << SHIFT, R_THRESH = 30; //One=1024,1左移10位2*10,R_THRESH是起始值,賦給max_count,后續會被覆蓋。
cv::Ptr<CvMat> dx, dy; //Ptr是智能指針模板,將CvMat對象封裝成指針
cv::Ptr<CvMat> edges, accum, dist_buf;//edges邊緣二值圖像,accum為累加器圖像,dist_buf存放候選圓心到滿足條件的邊緣點的半徑
std::vector<int> sort_buf;//用來進行排序的中間對象。在adata累加器排序中,其存放的是offset即偏移位置,int型。在ddata距離排序中,其存儲的和下標是一樣的值。
cv::Ptr<CvMemStorage> storage;//內存存儲器。創建的序列用來向其申請內存空間。
int x, y, i, j, k, center_count, nz_count;//center_count為圓心數,nz_count為非零數
float min_radius2 = (float)min_radius*min_radius;//最小半徑的平方
float max_radius2 = (float)max_radius*max_radius;//最大半徑的平方
int rows, cols, arows,acols;//rows,cols邊緣圖像的行數和列數,arows,acols是累加器圖像的行數和列數
int astep, *adata;//adata指向累加器數據域的首地址,用位置作為下標,astep為累加器每行的大小,以字節為單位
float* ddata;//ddata即dist_data,距離數據
CvSeq *nz, *centers;//nz為非0,即邊界,centers為存放的候選中心的位置。
float idp, dr;//idp即inv_dp,dp的倒數
CvSeqReader reader;//順序讀取序列中的每個值
edges = cvCreateMat( img->rows, img->cols, CV_8UC1 );//邊緣圖像
cvCanny( img, edges, MAX(canny_threshold/2,1), canny_threshold, 3 );//調用canny,變為二值圖像,0和非0即0和255
dx = cvCreateMat( img->rows, img->cols, CV_16SC1 );//16位單通道圖像,用來存儲二值邊緣圖像的x方向的一階導數
dy = cvCreateMat( img->rows, img->cols, CV_16SC1 );//y方向的
cvSobel( img, dx, 1, 0, 3 );//計算x方向的一階導數
cvSobel( img, dy, 0, 1, 3 );//計算y方向的一階導數
if( dp < 1.f )//控制dp不能比1小
dp = 1.f;
idp = 1.f/dp;
accum = cvCreateMat( cvCeil(img->rows*idp)+2, cvCeil(img->cols*idp)+2, CV_32SC1 );//cvCeil返回不小於參數的最小整數。32為單通道
cvZero(accum);//初始化累加器為0
storage = cvCreateMemStorage();//創建內存存儲器,使用默認參數0.默認大小為64KB
nz = cvCreateSeq( CV_32SC2, sizeof(CvSeq), sizeof(CvPoint), storage );//創建序列,用來存放非0點
centers = cvCreateSeq( CV_32SC1, sizeof(CvSeq), sizeof(int), storage );//用來存放圓心
rows = img->rows;
cols = img->cols;
arows = accum->rows - 2;
acols = accum->cols - 2;
adata = accum->data.i;//cvMat對象的union對象的i成員成員
//step是矩陣中行的長度,單位為字節。我們使用到的矩陣是accum它的深度是CV_32SC1即32位的int 型。
//如果我們知道一個指針如int* p;指向數組中的一個元素, 則可以通過p+accum->step/adata[0]來使指針移動到p指針所指元素的,正對的下一行元素
astep = accum->step/sizeof(adata[0]);
for( y = 0; y < rows; y++ )
{
const uchar* edges_row = edges->data.ptr + y*edges->step; //邊界存儲的矩陣的每一行的指向行首的指針。
const short* dx_row = (const short*)(dx->data.ptr + y*dx->step);//存儲 x方向sobel一階導數的矩陣的每一行的指向第一個元素的指針
const short* dy_row = (const short*)(dy->data.ptr + y*dy->step);//y
//遍歷邊緣的二值圖像和偏導數的圖像
for( x = 0; x < cols; x++ )
{
float vx, vy;
int sx, sy, x0, y0, x1, y1, r, k;
CvPoint pt;
vx = dx_row[x];//訪問每一行的元素
vy = dy_row[x];
if( !edges_row[x] || (vx == 0 && vy == 0) )//如果在邊緣圖像(存儲邊緣的二值圖像)某一點如A(x0,y0)==0則對一下點進行操作。vx和vy同時為0,則下一個
continue;
float mag = sqrt(vx*vx+vy*vy);//求梯度圖像
assert( mag >= 1 );//如果mag為0,說明沒有邊緣點,則stop。這里用了assert宏定義
sx = cvRound((vx*idp)*ONE/mag);// vx為該點的水平梯度(梯度幅值已經歸一化);ONE為為了用整數運算代替浮點數引入的一個因子,為2^10
sy = cvRound((vy*idp)*ONE/mag);
x0 = cvRound((x*idp)*ONE);
y0 = cvRound((y*idp)*ONE);
for( k = 0; k < 2; k++ )//k=0在梯度方向,k=1在梯度反方向對累加器累加。這里之所以要反向,因為對於一個圓上一個點,從這個點沿着斜率的方向的,最小半徑到最大半徑。在圓的另一邊與其相對應的點,有對應的效果。
{
x1 = x0 + min_radius * sx;
y1 = y0 + min_radius * sy;
for( r = min_radius; r <= max_radius; x1 += sx, y1 += sy, r++ )//x1=x1+sx即,x1=x0+min_radius*sx+sx=x0+(min_radius+1)*sx求得下一個點。sx為斜率
{
int x2 = x1 >> SHIFT, y2 = y1 >> SHIFT; //變回真實的坐標
if( (unsigned)x2 >= (unsigned)acols || //如果x2大於累加器的行
(unsigned)y2 >= (unsigned)arows )
break;
adata[y2*astep + x2]++;//由於c語言是按行存儲的。即等價於對accum數組進行了操作。
}
sx = -sx; sy = -sy;
}
pt.x = x; pt.y = y;
cvSeqPush( nz, &pt );//把非零邊緣並且梯度不為0的點壓入到堆棧
}
}
nz_count = nz->total;
if( !nz_count )//如果nz_count==0則返回
return;
for( y = 1; y < arows - 1; y++ ) //這里是從1到arows-1,因為如果是圓的話,那么圓的半徑至少為1,即圓心至少在內層里面
{
for( x = 1; x < acols - 1; x++ )
{
int base = y*(acols+2) + x;//計算位置,在accum圖像中
if( adata[base] > acc_threshold &&
adata[base] > adata[base-1] && adata[base] > adata[base+1] &&
adata[base] > adata[base-acols-2] && adata[base] > adata[base+acols+2] )
cvSeqPush(centers, &base);//候選中心點位置壓入到堆棧。其候選中心點累加數大於閾值,其大於四個鄰域
}
}
center_count = centers->total;
if( !center_count ) //如果沒有符合條件的圓心,則返回到函數。
return;
sort_buf.resize( MAX(center_count,nz_count) );//重新分配容器的大小,取候選圓心的個數和非零邊界的個數的最大值。因為后面兩個均用到排序。
cvCvtSeqToArray( centers, &sort_buf[0] ); //把序列轉換成數組,即把序列centers中的數據放入到sort_buf的容器中。
icvHoughSortDescent32s( &sort_buf[0], center_count, adata );//快速排序,根據sort_buf中的值作為下標,依照adata中對應的值進行排序,將累加值大的下標排到前面
cvClearSeq( centers );//清空序列
cvSeqPushMulti( centers, &sort_buf[0], center_count );//重新將中心的下標存入centers
dist_buf = cvCreateMat( 1, nz_count, CV_32FC1 );//創建一個32為浮點型的一個行向量
ddata = dist_buf->data.fl;//使ddata執行這個行向量的首地址
dr = dp;
min_dist = MAX( min_dist, dp );//如果輸入的最小距離小於dp,則設在為dp
min_dist *= min_dist;
for( i = 0; i < centers->total; i++ ) //對於每一個中心點
{
int ofs = *(int*)cvGetSeqElem( centers, i );//獲取排序的中心位置,adata值最大的元素,排在首位 ,offset偏移位置
y = ofs/(acols+2) - 1;//這里因為edge圖像比accum圖像小兩個邊。
x = ofs - (y+1)*(acols+2) - 1;//求得y坐標
float cx = (float)(x*dp), cy = (float)(y*dp);
float start_dist, dist_sum;
float r_best = 0, c[3];
int max_count = R_THRESH;
for( j = 0; j < circles->total; j++ )//中存儲已經找到的圓;若當前候選圓心與其中的一個圓心距離<min_dist,則舍棄該候選圓心
{
float* c = (float*)cvGetSeqElem( circles, j );//獲取序列中的元素。
if( (c[0] - cx)*(c[0] - cx) + (c[1] - cy)*(c[1] - cy) < min_dist )
break;
}
if( j < circles->total )//當前候選圓心與任意已檢測的圓心距離不小於min_dist時,才有j==circles->total
continue;
cvStartReadSeq( nz, &reader );
for( j = k = 0; j < nz_count; j++ )//每個候選圓心,對於所有的點
{
CvPoint pt;
float _dx, _dy, _r2;
CV_READ_SEQ_ELEM( pt, reader );
_dx = cx - pt.x; _dy = cy - pt.y; //中心點到邊界的距離
_r2 = _dx*_dx + _dy*_dy;
if(min_radius2 <= _r2 && _r2 <= max_radius2 )
{
ddata[k] = _r2; //把滿足的半徑的平方存起來
sort_buf[k] = k;//sort_buf同上,但是這里的sort_buf的下標值和元素值是相同的,重新利用
k++;//k和j是兩個游標
}
}
int nz_count1 = k, start_idx = nz_count1 - 1;
if( nz_count1 == 0 )
continue; //如果一個候選中心到(非零邊界且梯度>0)確定的點的距離中,沒有滿足條件的,則從下一個中心點開始。
dist_buf->cols = nz_count1;//用來存放真是的滿足條件的非零元素(三個約束:非零點,梯度不為0,到圓心的距離在min_radius和max_radius中間)
cvPow( dist_buf, dist_buf, 0.5 );//對dist_buf中的元素開根號.求得半徑
icvHoughSortDescent32s( &sort_buf[0], nz_count1, (int*)ddata );////對與圓心的距離按降序排列,索引值在sort_buf中
dist_sum = start_dist = ddata[sort_buf[nz_count1-1]];//dist距離,選取半徑最小的作為起始值
//下邊for循環里面是一個算法。它定義了兩個游標(指針)start_idx和j,j是外層循環的控制變量。而start_idx為控制當兩個相鄰的數組ddata的數據發生變化時,即d-start_dist>dr時,的步進。
for( j = nz_count1 - 2; j >= 0; j-- )//從小到大。選出半徑支持點數最多的半徑
{
float d = ddata[sort_buf[j]];
if( d > max_radius )//如果求得的候選圓點到邊界的距離大於參數max_radius,則停止,因為d是第一個出現的最小的(按照從大到小的順序排列的)
break;
if( d - start_dist > dr )//如果當前的距離減去最小的>dr(==dp)
{
float r_cur = ddata[sort_buf[(j + start_idx)/2]];//當前半徑設為符合該半徑的中值,j和start_idx相當於兩個游標
if( (start_idx - j)*r_best >= max_count*r_cur || //如果數目相等時,它會找半徑較小的那個。這里是判斷支持度的算法
(r_best < FLT_EPSILON && start_idx - j >= max_count) ) //程序這個部分告訴我們,無法找到同心圓,它會被外層最大,支持度最多(支持的點最多)所覆蓋。
{
r_best = r_cur;//如果 符合當前半徑的點數(start_idx - j)/ 當前半徑>= 符合之前最優半徑的點數/之前的最優半徑 || 還沒有最優半徑時,且點數>30時;其實直接把r_best初始值置為1即可省去第二個條件
max_count = start_idx - j;//maxcount變為符合當前半徑的點數,更新max_count值,后續的支持度大的半徑將會覆蓋前面的值。
}
start_dist = d;
start_idx = j;
dist_sum = 0;//如果距離改變較大,則重置distsum為0,再在下面的式子中置為當前值
}
dist_sum += d;//如果距離改變較小,則加上當前值(dist_sum)在這里好像沒有用處。
}
if( max_count > R_THRESH )//符合條件的圓周點大於閾值30,則將圓心、半徑壓棧
{
c[0] = cx;
c[1] = cy;
c[2] = (float)r_best;
cvSeqPush( circles, c );
if( circles->total > circles_max )//circles_max是個很大的數,其值為INT_MAX
return;
}
}
}
CV_IMPL CvSeq*
cvHoughCircles1( CvArr* src_image, void* circle_storage,
int method, double dp, double min_dist,
double param1, double param2,
int min_radius, int max_radius )
{
CvSeq* result = 0;
CvMat stub, *img = (CvMat*)src_image;
CvMat* mat = 0;
CvSeq* circles = 0;
CvSeq circles_header;
CvSeqBlock circles_block;
int circles_max = INT_MAX;
int canny_threshold = cvRound(param1);//cvRound返回和參數最接近的整數值,對一個double類型進行四舍五入
int acc_threshold = cvRound(param2);
img = cvGetMat( img, &stub );//將img轉化成為CvMat對象
if( !CV_IS_MASK_ARR(img)) //圖像必須為8位,單通道圖像
CV_Error( CV_StsBadArg, "The source image must be 8-bit, single-channel" );
if( !circle_storage )
CV_Error( CV_StsNullPtr, "NULL destination" );
if( dp <= 0 || min_dist <= 0 || canny_threshold <= 0 || acc_threshold <= 0 )
CV_Error( CV_StsOutOfRange, "dp, min_dist, canny_threshold and acc_threshold must be all positive numbers" );
min_radius = MAX( min_radius, 0 );
if( max_radius <= 0 )//用來控制當使用默認參數max_radius=0的時候
max_radius = MAX( img->rows, img->cols );
else if( max_radius <= min_radius )
max_radius = min_radius + 2;
if( CV_IS_STORAGE( circle_storage ))//如果傳入的是內存存儲器
{
circles = cvCreateSeq( CV_32FC3, sizeof(CvSeq),
sizeof(float)*3, (CvMemStorage*)circle_storage );
}
else if( CV_IS_MAT( circle_storage ))//如果傳入的參數時數組
{
mat = (CvMat*)circle_storage;
//數組應該是CV_32FC3類型的單列數組。
if( !CV_IS_MAT_CONT( mat->type ) || (mat->rows != 1 && mat->cols != 1) ||//連續,單列,CV_32FC3類型
CV_MAT_TYPE(mat->type) != CV_32FC3 )
CV_Error( CV_StsBadArg,
"The destination matrix should be continuous and have a single row or a single column" );
//將數組轉換為序列
circles = cvMakeSeqHeaderForArray( CV_32FC3, sizeof(CvSeq), sizeof(float)*3,
mat->data.ptr, mat->rows + mat->cols - 1, &circles_header, &circles_block );//由於是單列,故elem_size為mat->rows+mat->cols-1
circles_max = circles->total;
cvClearSeq( circles );//清空序列的內容(如果傳入的有數據的話)
}
else
CV_Error( CV_StsBadArg, "Destination is not CvMemStorage* nor CvMat*" );
switch( method )
{
case CV_HOUGH_GRADIENT:
icvHoughCirclesGradient( img, (float)dp, (float)min_dist,
min_radius, max_radius, canny_threshold,
acc_threshold, circles, circles_max );
break;
default:
CV_Error( CV_StsBadArg, "Unrecognized method id" );
}
if( mat )//給定一個指向圓存儲的數組指針值,則返回0,即NULL
{
if( mat->cols > mat->rows )//因為不知道傳入的是列向量還是行向量。
mat->cols = circles->total;
else
mat->rows = circles->total;
}
else//如果是傳入的是內存存儲器,則返回一個指向一個序列的指針。
result = circles;
return result;
}
8.2 version2:(趙老師)
static void
icvHoughCirclesGradient( CvMat* img, float dp, float min_dist,
int min_radius, int max_radius,
int canny_threshold, int acc_threshold,
CvSeq* circles, int circles_max )
{
//為了提高運算精度,定義一個數值的位移量
const int SHIFT = 10, ONE = 1 << SHIFT;
//定義水平梯度和垂直梯度矩陣的地址指針
cv::Ptr<CvMat> dx, dy;
//定義邊緣圖像、累加器矩陣和半徑距離矩陣的地址指針
cv::Ptr<CvMat> edges, accum, dist_buf;
//定義排序向量
std::vector<int> sort_buf;
cv::Ptr<CvMemStorage> storage;
int x, y, i, j, k, center_count, nz_count;
//事先計算好最小半徑和最大半徑的平方
float min_radius2 = (float)min_radius*min_radius;
float max_radius2 = (float)max_radius*max_radius;
int rows, cols, arows, acols;
int astep, *adata;
float* ddata;
//nz表示圓周序列,centers表示圓心序列
CvSeq *nz, *centers;
float idp, dr;
CvSeqReader reader;
//創建一個邊緣圖像矩陣
edges = cvCreateMat( img->rows, img->cols, CV_8UC1 );
//第一階段
//步驟1.1,用canny邊緣檢測算法得到輸入圖像的邊緣圖像
cvCanny( img, edges, MAX(canny_threshold/2,1), canny_threshold, 3 );
//創建輸入圖像的水平梯度圖像和垂直梯度圖像
dx = cvCreateMat( img->rows, img->cols, CV_16SC1 );
dy = cvCreateMat( img->rows, img->cols, CV_16SC1 );
//步驟1.2,用Sobel算子法計算水平梯度和垂直梯度
cvSobel( img, dx, 1, 0, 3 );
cvSobel( img, dy, 0, 1, 3 );
/確保累加器矩陣的分辨率不小於1
if( dp < 1.f )
dp = 1.f;
//分辨率的倒數
idp = 1.f/dp;
//根據分辨率,創建累加器矩陣
accum = cvCreateMat( cvCeil(img->rows*idp)+2, cvCeil(img->cols*idp)+2, CV_32SC1 );
//初始化累加器為0
cvZero(accum);
//創建兩個序列,
storage = cvCreateMemStorage();
nz = cvCreateSeq( CV_32SC2, sizeof(CvSeq), sizeof(CvPoint), storage );
centers = cvCreateSeq( CV_32SC1, sizeof(CvSeq), sizeof(int), storage );
rows = img->rows; //圖像的高
cols = img->cols; //圖像的寬
arows = accum->rows - 2; //累加器的高
acols = accum->cols - 2; //累加器的寬
adata = accum->data.i; //累加器的地址指針
astep = accum->step/sizeof(adata[0]); /累加器的步長
// Accumulate circle evidence for each edge pixel
//步驟1.3,對邊緣圖像計算累加和
for( y = 0; y < rows; y++ )
{
//提取出邊緣圖像、水平梯度圖像和垂直梯度圖像的每行的首地址
const uchar* edges_row = edges->data.ptr + y*edges->step;
const short* dx_row = (const short*)(dx->data.ptr + y*dx->step);
const short* dy_row = (const short*)(dy->data.ptr + y*dy->step);
for( x = 0; x < cols; x++ )
{
float vx, vy;
int sx, sy, x0, y0, x1, y1, r;
CvPoint pt;
//當前的水平梯度值和垂直梯度值
vx = dx_row[x];
vy = dy_row[x];
//如果當前的像素不是邊緣點,或者水平梯度值和垂直梯度值都為0,則繼續循環。因為如果滿足上面條件,該點一定不是圓周上的點
if( !edges_row[x] || (vx == 0 && vy == 0) )
continue;
//計算當前點的梯度值
float mag = sqrt(vx*vx+vy*vy);
assert( mag >= 1 );
//定義水平和垂直的位移量
sx = cvRound((vx*idp)*ONE/mag);
sy = cvRound((vy*idp)*ONE/mag);
//把當前點的坐標定位到累加器的位置上
x0 = cvRound((x*idp)*ONE);
y0 = cvRound((y*idp)*ONE);
// Step from min_radius to max_radius in both directions of the gradient
//在梯度的兩個方向上進行位移,並對累加器進行投票累計
for(int k1 = 0; k1 < 2; k1++ )
{
//初始一個位移的啟動
//位移量乘以最小半徑,從而保證了所檢測的圓的半徑一定是大於最小半徑
x1 = x0 + min_radius * sx;
y1 = y0 + min_radius * sy;
//在梯度的方向上位移
// r <= max_radius保證了所檢測的圓的半徑一定是小於最大半徑
for( r = min_radius; r <= max_radius; x1 += sx, y1 += sy, r++ )
{
int x2 = x1 >> SHIFT, y2 = y1 >> SHIFT;
//如果位移后的點超過了累加器矩陣的范圍,則退出
if( (unsigned)x2 >= (unsigned)acols ||
(unsigned)y2 >= (unsigned)arows )
break;
//在累加器的相應位置上加1
adata[y2*astep + x2]++;
}
//把位移量設置為反方向
sx = -sx; sy = -sy;
}
//把輸入圖像中的當前點(即圓周上的點)的坐標壓入序列圓周序列nz中
pt.x = x; pt.y = y;
cvSeqPush( nz, &pt );
}
}
//計算圓周點的總數
nz_count = nz->total;
//如果總數為0,說明沒有檢測到圓,則退出該函數
if( !nz_count )
return;
//Find possible circle centers
//步驟1.4和1.5,遍歷整個累加器矩陣,找到可能的圓心
for( y = 1; y < arows - 1; y++ )
{
for( x = 1; x < acols - 1; x++ )
{
int base = y*(acols+2) + x;
//如果當前的值大於閾值,並在4鄰域內它是最大值,則該點被認為是圓心
if( adata[base] > acc_threshold &&
adata[base] > adata[base-1] && adata[base] > adata[base+1] &&
adata[base] > adata[base-acols-2] && adata[base] > adata[base+acols+2] )
//把當前點的地址壓入圓心序列centers中
cvSeqPush(centers, &base);
}
}
//計算圓心的總數
center_count = centers->total;
//如果總數為0,說明沒有檢測到圓,則退出該函數
if( !center_count )
return;
//定義排序向量的大小
sort_buf.resize( MAX(center_count,nz_count) );
//把圓心序列放入排序向量中
cvCvtSeqToArray( centers, &sort_buf[0] );
//對圓心按照由大到小的順序進行排序
//它的原理是經過icvHoughSortDescent32s函數后,以sort_buf中元素作為adata數組下標,adata中的元素降序排列,即adata[sort_buf[0]]是adata所有元素中最大的,adata[sort_buf[center_count-1]]是所有元素中最小的
icvHoughSortDescent32s( &sort_buf[0], center_count, adata );
//清空圓心序列
cvClearSeq( centers );
//把排好序的圓心重新放入圓心序列中
cvSeqPushMulti( centers, &sort_buf[0], center_count );
//創建半徑距離矩陣
dist_buf = cvCreateMat( 1, nz_count, CV_32FC1 );
//定義地址指針
ddata = dist_buf->data.fl;
dr = dp; //定義圓半徑的距離分辨率
//重新定義圓心之間的最小距離
min_dist = MAX( min_dist, dp );
//最小距離的平方
min_dist *= min_dist;
// For each found possible center
// Estimate radius and check support
//按照由大到小的順序遍歷整個圓心序列
for( i = 0; i < centers->total; i++ )
{
//提取出圓心,得到該點在累加器矩陣中的偏移量
int ofs = *(int*)cvGetSeqElem( centers, i );
//得到圓心在累加器中的坐標位置
y = ofs/(acols+2);
x = ofs - (y)*(acols+2);
//Calculate circle's center in pixels
//計算圓心在輸入圖像中的坐標位置
float cx = (float)((x + 0.5f)*dp), cy = (float)(( y + 0.5f )*dp);
float start_dist, dist_sum;
float r_best = 0;
int max_count = 0;
// Check distance with previously detected circles
//判斷當前的圓心與之前確定作為輸出的圓心是否為同一個圓心
for( j = 0; j < circles->total; j++ )
{
//從序列中提取出圓心
float* c = (float*)cvGetSeqElem( circles, j );
//計算當前圓心與提取出的圓心之間的距離,如果兩者距離小於所設的閾值,則認為兩個圓心是同一個圓心,退出循環
if( (c[0] - cx)*(c[0] - cx) + (c[1] - cy)*(c[1] - cy) < min_dist )
break;
}
//如果j < circles->total,說明當前的圓心已被認為與之前確定作為輸出的圓心是同一個圓心,則拋棄該圓心,返回上面的for循環
if( j < circles->total )
continue;
// Estimate best radius
//第二階段
//開始讀取圓周序列nz
cvStartReadSeq( nz, &reader );
for( j = k = 0; j < nz_count; j++ )
{
CvPoint pt;
float _dx, _dy, _r2;
CV_READ_SEQ_ELEM( pt, reader );
_dx = cx - pt.x; _dy = cy - pt.y;
//步驟2.1,計算圓周上的點與當前圓心的距離,即半徑
_r2 = _dx*_dx + _dy*_dy;
//步驟2.2,如果半徑在所設置的最大半徑和最小半徑之間
if(min_radius2 <= _r2 && _r2 <= max_radius2 )
{
//把半徑存入dist_buf內
ddata[k] = _r2;
sort_buf[k] = k;
k++;
}
}
//k表示一共有多少個圓周上的點
int nz_count1 = k, start_idx = nz_count1 - 1;
//nz_count1等於0也就是k等於0,說明當前的圓心沒有所對應的圓,意味着當前圓心不是真正的圓心,所以拋棄該圓心,返回上面的for循環
if( nz_count1 == 0 )
continue;
dist_buf->cols = nz_count1; //得到圓周上點的個數
cvPow( dist_buf, dist_buf, 0.5 ); //求平方根,得到真正的圓半徑
//步驟2.3,對圓半徑進行排序
icvHoughSortDescent32s( &sort_buf[0], nz_count1, (int*)ddata );
dist_sum = start_dist = ddata[sort_buf[nz_count1-1]];
//步驟2.4
for( j = nz_count1 - 2; j >= 0; j-- )
{
float d = ddata[sort_buf[j]];
if( d > max_radius )
break;
//d表示當前半徑值,start_dist表示上一次通過下面if語句更新后的半徑值,dr表示半徑距離分辨率,如果這兩個半徑距離之差大於距離分辨率,說明這兩個半徑一定不屬於同一個圓,而兩次滿足if語句條件之間的那些半徑值可以認為是相等的,即是屬於同一個圓
if( d - start_dist > dr )
{
//start_idx表示上一次進入if語句時更新的半徑距離排序的序號
// start_idx – j表示當前得到的相同半徑距離的數量
//(j + start_idx)/2表示j和start_idx中間的數
//取中間的數所對應的半徑值作為當前半徑值r_cur,也就是取那些半徑值相同的值
float r_cur = ddata[sort_buf[(j + start_idx)/2]];
//如果當前得到的半徑相同的數量大於最大值max_count,則進入if語句
if( (start_idx - j)*r_best >= max_count*r_cur ||
(r_best < FLT_EPSILON && start_idx - j >= max_count) )
{
r_best = r_cur; //把當前半徑值作為最佳半徑值
max_count = start_idx - j; //更新最大值
}
//更新半徑距離和序號
start_dist = d;
start_idx = j;
dist_sum = 0;
}
dist_sum += d;
}
// Check if the circle has enough support
//步驟2.5,最終確定輸出
//如果相同半徑的數量大於所設閾值
if( max_count > acc_threshold )
{
float c[3];
c[0] = cx; //圓心的橫坐標
c[1] = cy; //圓心的縱坐標
c[2] = (float)r_best; //所對應的圓的半徑
cvSeqPush( circles, c ); //壓入序列circles內
//如果得到的圓大於閾值,則退出該函數
if( circles->total > circles_max )
return;
}
}
}
9 參考文章
https://blog.csdn.net/qq_37059483/article/details/77916655
https://blog.csdn.net/m0_37264397/article/details/72729423
https://blog.csdn.net/zhaocj/article/details/50454847
https://blog.csdn.net/shanchuan2012/article/details/74010561
http://www.cnblogs.com/AndyJee/p/3805594.html
https://blog.csdn.net/cy513/article/details/4269340
https://blog.csdn.net/poem_qianmo/article/details/26977557
http://homepages.inf.ed.ac.uk/rbf/HIPR2/hough.htm
https://blog.csdn.net/m0_37264397/article/details/72729423
https://www.cnblogs.com/AndyJee/p/3805594.html
