1. 為什么要使用正則化
我們先回顧一下房價預測的例子。以下是使用多項式回歸來擬合房價預測的數據:
可以看出,左圖擬合較為合適,而右圖過擬合。如果想要解決右圖中的過擬合問題,需要能夠使得 $ x^3,x^4 $ 的參數 $ \theta_3,\theta_4 $ 盡量滿足 $ \theta_3 \approx 0 ,\theta_4 \approx 0 $ 。 而如何使得 $ \theta_3,\theta_4 $ 盡可能接近 $ 0 $ 呢?那就是對參數施一懲罰項。我們先來看一下線性回歸的代價函數: $$ J(\theta) = \frac{1}{2m} \sum_{i=1}^{n} (h_\theta(x^{(i)})-y^{(i)})^2 $$ 如果對參數施加懲罰項,式子變為: $$ J(\theta) = \frac{1}{2m} \sum_{i=1}^{n} (h_\theta(x^{(i)})-y^{(i)})^2 + \lambda \sum_{j=0}^{k}\theta_j^2 $$ 梯度下降的式子變為: $$ \theta_j := \theta_j - \lambda\frac{\Delta J(\theta)}{\Delta \theta_j} $$ 我們對梯度下降的式子進行推導一下:
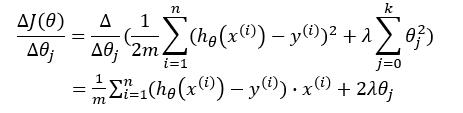
故: $$ \theta_j := \theta_j - [ \frac{1}{m} \sum_{i=1}^{n}(h_\theta(x^{(i)})-y^{(i)})^2 + 2 \lambda \theta_j ] $$
由上可以看出,當正則項系數 $ \lambda $ 很大時,對參數的懲罰也將很大,導致在梯度更新后對應的 $ \theta_j $ 值很小。由此可以使得對某些參數最終接近於 $ 0 $ 。而正則項系數 $ \lambda $ 即為模型復雜度的懲罰項,當其很大時,模型復雜度將變小,也就是模型將更為簡單,不會使得對數據過於擬合。
從結構風險最小化角度來說,就是在經驗風險最小化的基礎上(即訓練誤差最小化),盡可能采用簡單的模型,以此提高泛化預測精度。
這一小節我們直觀地了解了為何要使用正則化項,接下來我們從理論上來分析一下。
2. L1正則化與L2正則化
這一小節參考自博客1。
依舊以線性回歸為例(只含有兩個參數的情況,此處的參數 $ w $ 與上一節中的 $ \theta $ 一致,只是本節中為了與圖片上的參數相對應,而將參數使用 $ w $ 進行表示)。加上L1正則化后的優化目標(lasso回歸): $$ min \frac{1}{2m} \sum_{i=1}^{n} (h_w(x^{(i)})-y^{(i)})^2 + \lambda \sum_{j=1}^{2} |w_j| $$
加上L2正則化后的優化目標(嶺回歸): $$ min \frac{1}{2m} \sum_{i=1}^{n} (h_w(x^{(i)})-y^{(i)})^2 + \lambda \sum_{j=1}^{2}w_j^2 $$
使用等高線圖來表示原目標函數的圖像為:
也就是說,當參數 $ w_1 與 w_2 $ 取值為圖像中最里面那個紫色圓圈上的值時,可以使得原目標函數最小。 當加上L1正則項之后,目標函數圖像為:
當加上L2正則項之后,目標函數圖像為:
第一個圖中菱形即為 $ \sum_{j=1}^{2}|w_j| = F $ ,而第二個圖中圓形即為 $ \sum_{j=1}^{2}w_j^2 = F $ 。代表這個菱形(圓形)上的點算出來的 $ \sum_{j=1}^{2}|w_j| 或 \sum_{j=1}^{2}w_j^2 $ 都等於某個值 $ F $ 。此時若要使得目標函數最小,就需要滿足兩個條件:(1)參數值在等高線上的圓圈越來越接近中心的紫色圓圈,(2)菱形越小越好( $ F $ 越小越好)。 那么如何取得一個恰好的值,能夠滿足以上兩個條件呢?我們先來看下下面這個圖(以L1正則化為例):

以**同一條原曲線目標等高線**來說,現在以最外圈的紅色等高線為例,我們看到,對於紅色曲線上的每個點都可以做一個菱形,根據上圖可知,當這個菱形與某條等高線相切(僅有一個交點)的時候,這個菱形最小,上圖相割對比較大的兩個菱形對應的L1正則化項更大。也就是說,相切時在使得 $ \frac{1}{2m} \sum_{i=1}^{n} (h_w(x^{(i)})-y^{(i)})^2 $ 相同的情況下, $ \lambda \sum_{j=1}^{2}|w_j| $ 最小,因此,該點能夠使得 $ \frac{1}{2m} \sum_{i=1}^{n} (h_w(x^{(i)})-y^{(i)})^2 + \lambda \sum_{j=1}^{2} |w_j| $ 最小。 由以上結論,我們可以看出,要使得加入L1正則化的解,一定是某個菱形和某條原函數等高線的切點。而通過觀察我們可以看出,**幾乎對於很多原函數等高曲線,和某個菱形相交的時候及其容易相交在坐標軸(比如上圖),也就是說最終的結果,解的某些維度及其容易是 $ 0 $ ,比如上圖最終解是 $ w = (0,x)$ ,這也就是我們所說的L1更容易得到稀疏解(解向量中0比較多)的原因。** 接下來我們使用公式進行推導一下看。假設現在是在一維的情況下,目標函數看做是 $ J(w) = f(w) + \lambda |w| $ ,其中 $ f(w) $ 為原目標函數, $ J(w) $ 為加了L1正則項之后的目標函數。 $ \lambda |w| $ 是正則化項。那么要使得 $ 0 $ 點成為最值可能的點,即使在 $ 0 $ 點不可導,但是只需要讓函數在 $ 0 $ 點左右的導數異號。即 $ J'_左(w) \times J'_右(w) = (f'(0) + \lambda) \times (f'(0) - \lambda) < 0 $ ,也就是 $ \lambda > |f'(0)| $ 時, $ 0 $ 點都是可能的最值點。 當加入L2正則化的時候,分析和L1正則化是類似的,也就是說我們僅僅是從菱形變成了圓形而已,同樣還是求原曲線和圓形的切點作為最終解。當然與L1范數比,我們這樣求的L2范數的從圖上來看,不容易交在坐標軸上,但是仍然比較靠近坐標軸。因此這也就是我們老說的,L2范數能讓解比較小(靠近0),但是比較平滑(不等於0)。 **綜上所述,我們可以看見,加入正則化項,在最小化經驗誤差的情況下,可以讓我們選擇解更簡單(趨向於0)的解。因此,加正則化項就是結構風險最小化的一種實現。**
引用及參考:
[1] https://zhuanlan.zhihu.com/p/35356992?utm_medium=social&utm_source=wechat_session
[2] https://blog.csdn.net/pakko/article/details/37878837
[3] https://www.zhihu.com/question/37096933/answer/70426653
寫在最后:本文參考以上資料進行整合與總結,屬於原創,文章中可能出現理解不當的地方,若有所見解或異議可在下方評論,謝謝!
若需轉載請注明:https://www.cnblogs.com/lliuye/p/9354972.html





