K好數--藍橋杯

JAVA版K好數--藍橋杯

歷經千辛萬苦，也算是研究出來了這道題了。

這道題主要運用了動態規划(Dynamic Planning)的思想，何謂動態規划？其實就是將一個大問題分成一個個小問題，然后先通過把各個小問題都解決，自然而然大問題也就解決了。

這道題它問L位K進制中，有多少K好數(任意相鄰兩位數字不相臨)

---

我的理解： K進制的意思是它每一位的組成只能從(0~K-1)中選取，如果你想直接求L位長的K進制數有多少K好數，可能有些復雜，不如先求1位長，再通過1位長求2位長……以此類推，便可以通過累加得出L位長的K好數總共有多少。

先上代碼

   public static void KGoodNumber() {
        Scanner sc = new Scanner(System.in);
        long mod = 1000000007;
        int radix = sc.nextInt();
        int length = sc.nextInt();
        long dp[][] = new long[length][jinzhi];
        //二維數組第一維是表示長度，第二維表示該長度下開頭的數字，該數組的值為滿足前二條件的K好數的個數
        for (int i = 0; i < radix; i++) {
            dp[0][i] = 1;
        }
        for (int m = 1; m < length; m++) {
            for (int j = 0; j < radix; j++) {
                for (int x = 0; x < radix; x++) {
                    if (x != j + 1 && x != j - 1) {
           				//如果m位長的開頭為j，m-1位長開頭為x，並且x與j不相臨
                        ** dp[m][j] += dp[m - 1][x];
                           dp[m][j] %= mod;
                    }
                }
            }
        }
        long sum = 0;
        //由於K好數不能以0開頭，所以從1開始取
        for (int y = 1; y < radix; y++) {
            sum += dp[length - 1][y];
            sum %= mod;
        }
        System.out.println(sum);
    }

上個圖來解釋一下

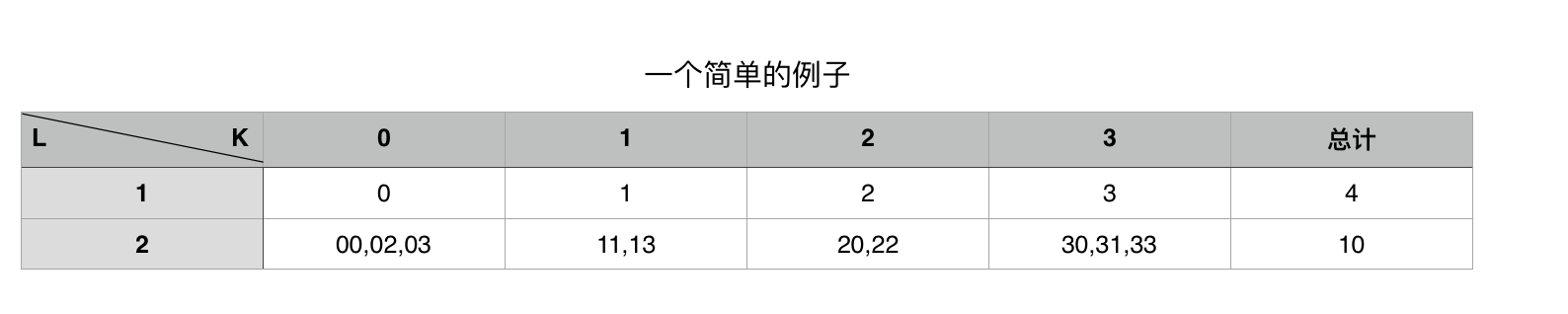
圖中L為長度 K為進制數，上面的圖簡單說明了 4進制 如何由 L=1的K好數推導出L=2的K好數。

我想借助這個圖來說明上面由**標示的語句

這道題約束條件是任意兩位數字不能相臨，那么，我們就讓它從L=1時的K好數和L=2時首數字與L=1的那個K好數的首數字不相臨，那么這個L=2的數也就是K好數。依此類推。

最后要說的就是K好數的開頭不能為零。所以計算長為L，由1~N-1開頭的K好數的總和，即為本題的答案。

update by 2017/4/4 20:15

by 一枝豬