在上文中,我們聊到了離散傅里葉變換的實現,其時間復雜度是O(N^2),以及快速傅里葉變換的遞歸實現,其時間復雜度是O(NlogN)。
但是因為實現方式是用遞歸法,並且為了分離奇偶下標的數據,又重新申請了一些數組,所以空間復雜度有所上升,顯然不是最優解。分離奇偶下標的過程:
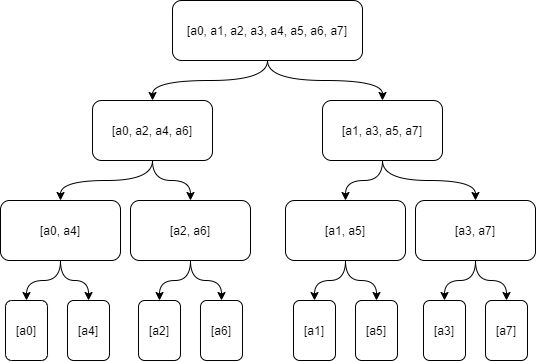
遞歸法是從最頂端開始,一層一層循環,不斷地拆分數組,到最底端。然后再一層層地做特殊運算,回到最頂端。
蝴蝶操作
上述這個特殊運算的操作叫做蝴蝶(butterfly)操作:

如上,譬如輸入兩個數 y[0]和y[1],經過一陣你中有我,我中有你的X型運算之后,輸出的依然是兩個數。
至於為什么叫蝴蝶運算,可能是這個叉叉的X型的形狀比較像蝴蝶吧:

繼續剛才我們說到的再一層層地做蝴蝶運算,回到最頂端的過程,如下圖:
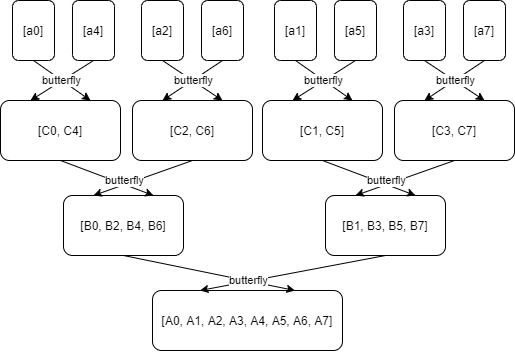
下圖展現了和上圖相同的意思,但是更加精確:
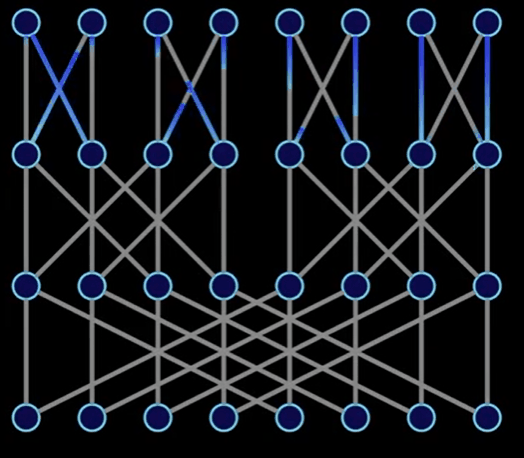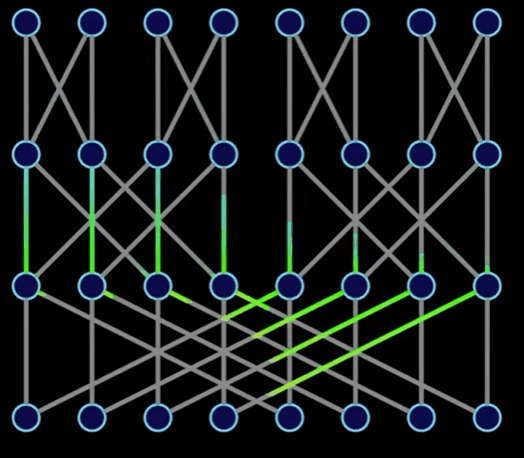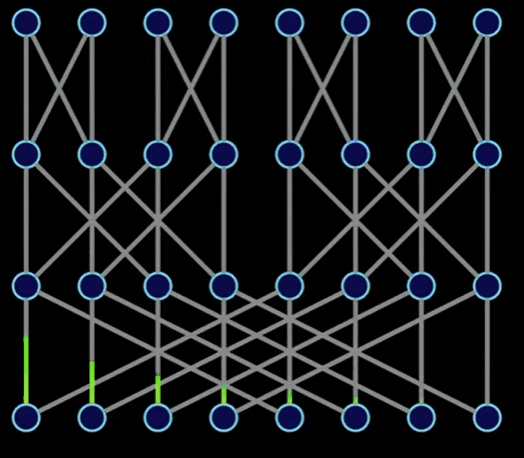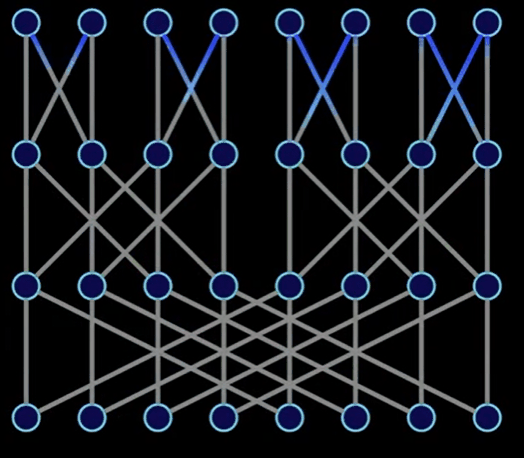
以上,我們發現有趣的一點:
[a0, a4, a2, a6, a1, a5, a3, a7] 這個數組轉換成結果 [A0, A1, A2, A3, A4, A5, A6, A7]。
這個計算的過程是可以原地進行的,這樣的話空間復雜度可以做到O(1)(幾乎不不需要額外的內存空間)。
位逆序(bit reverse)
為了達到這樣的效果,我們首先需要做的是:

其中規律已經有人研究出來了:位逆序 bit reverse這個規律,對於任何二次冪減一的數都管用。本文圖中僅以最大值7作為示例。
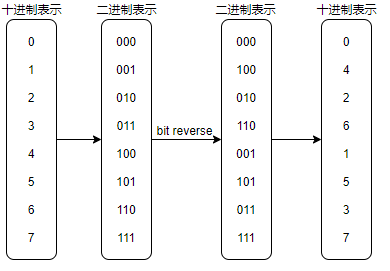
說道bit reverse,顯然這是一道leetcode題啊,參見leetcode第190題。
https://leetcode-cn.com/problems/reverse-bits/
點贊數最高的那個答案寫得更容易理解一點,於是直接拿來用下。不過因為我們的bits位數會有變化,不僅僅是32bits,也可能是8 bits或者是128 bits,所以稍加修改即可:
uint64_t reverseBits(uint64_t n, uint64_t bits) {
uint64_t res = 0;
for (uint64_t i = 0; i < bits; ++i) {
res = (res << 1) | (n & 1);
n >>= 1;
}
return res;
}
然后在arrayReorder中調用 reverseBits 對原數組中的數據進行調換:
void arrayReorder(vector<complex <double>> &data)
{
uint64_t x, r = log2(data.size());
for(uint64_t i = 0; i < data.size(); ++i){
x = reverseBits(i, r);
if (x > i){
swap(data[i], data[x]);
}
}
}
接着為我們就可以層層循環地進行FFT操作了,以下是我基於《算法導論》中的偽代碼,重寫得C++代碼(親測可用):
#include <stdio.h>
#include <stdlib.h>
#include <cstdint>
#include <iostream>
#include <complex>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
const double pi = acos(-1.0);
void fft_iter(vector<complex<double>>& data, bool inv)
{
complex<double> wn, deltawn, t, u;
uint64_t length = data.size();
uint64_t log2n = (length==0)?0:log2(length);
int64_t sign = inv?1:-1;
arrayReorder(data);
for (uint64_t i = 1; i <= log2n; ++i) //logn 次循環
{
uint64_t m = 1<<i;
deltawn = polar<double>(1, sign*2*pi/m);
for (uint64_t k = 0; k < length; k += m) //這個for和下面的for加起來,是n次循環
{
wn = polar<double>(1, 0);
for (uint64_t j = 0; j < m/2; j++)
{
t = data[k + j + m/2]*(wn);
u = data[k + j];
data[k + j] = u + t;
data[k + j + m/2]= u - t;
wn *= deltawn;
}
}
}
if (inv)
for (uint64_t i = 0; i < length; ++i)
data[i] /= length;
}
如果有對不同循環中的ω的值不一樣有所疑問,可以參考上一篇文章哈。
以上代碼,會發現時間復雜度依然是O(NlogN),但是空間復雜度是恆定的O(1)。在此,迭代法相較遞歸法又上升了一個台階,不得不感嘆算法的魔力。
對了,有傅里葉正變換,就有傅里葉逆變換,其區別就如離散傅里葉變換和離散傅里葉逆變換的公式區別:
離散傅里葉正變換:
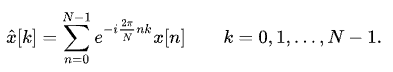
離散傅里葉逆變換:
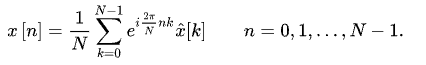
在上述代碼中,快速傅里葉正變換(時域轉換成頻域):
fft_iter(data, false);
快速傅里葉逆變換(頻域轉換成時域):
fft_iter(data, true);
本文中介紹的FFT算法,只針對序列長度為2次冪的DFT計算,即基2-FFT。並且本文介紹的只是FFT算法中的一種,即時域抽取dit(Decimation-in-time),加上是基2-FFT,所以該算法簡稱為DIT2。
這一系列說到現在,到底是誰讓傅里葉變換變快了的呢?FFT的基本思路是在1965年由J. W. Cooley和J. W. Tukey合作發表An algorithm for the machine calculation of complex Fourier series之后開始為人所知的。
DIT和DIF
在FFT算法中,針對輸入做不同方式的分組會造成輸出順序上的不同。如果我們使用時域抽取(Decimation-in-time),那么輸入的順序將會是比特反轉排列(bit-reversed order),輸出將會依序排列。但若我們采取的是頻域抽取(Decimation-in-frequency),那么輸出與輸出順序的情況將會完全相反,變為依序排列的輸入與比特反轉排列的輸出。
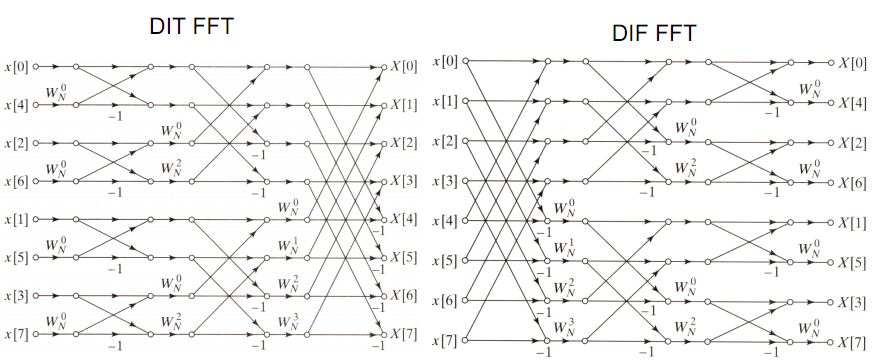
如上圖所示,本文的代碼是DIT FFT沒錯了。
FFT的知識深似海。如果您有興趣了解,可以參考比較通用的kissfft實現:
https://github.com/mborgerding/kissfft
或者速度更快的FFTW實現:
https://www.fftw.org/
我在想,也許我們大腦也有類似這樣的代碼回路吧,這樣我們才能區分高頻的尖叫和低頻的低音。
最后
傅里葉變換系列的文章寫到現在,因為本人水平有限,難免會有所紕漏,如果有存疑的地方,可以評論或加我好友交流,非常感謝你的閱讀!
