雙指針算法詳解
參考鏈接
練習題
相關鏈接
什么是雙指針
雙指針,指的是在遍歷對象的過程中,不是普通的使用單個指針[或者稱之為變量]進行訪問,而是使用兩個相同方向(快慢指針)或者相反方向(對撞指針)的指針進行掃描,從而達到相應的目的。
換言之,雙指針法充分使用了數組有序這一特征,從而在某些情況下能夠簡化一些運算。
在 LeetCode 題庫中,關於雙指針的問題還是挺多的。雙指針
雙指針從廣義上來說,是指用兩個變量在線性結構上遍歷而解決的問題。狹義上說,
- 對於數組,指兩個變量在數組上相向移動解決的問題;
- 對於鏈表,指兩個變量在鏈表上同向移動解決的問題,也稱為「快慢指針」問題。
雙指針算法通常不難,雙指針算法是基於暴力解法的優化,它們是很好的學習算法的入門問題,讓我們開始學習雙指針算法之旅吧。
快慢指針(Fast & Slow pointers)
基本原理及應用場景
快慢指針方法,又稱為龜兔賽跑算法,其基本思想就是使用兩個移動速度不同的指針(快指針是慢指針的X倍,X > 1)在數組或鏈表等序列結構上移動。這種方法對於處理「環形」鏈表或數組非常有用。以鏈表為例,通過以不同的速度移動,我們可以證明如果鏈表中存在環,則兩個指針必定會相遇,當兩個指針均處在環中時,快指針會追上慢指針(如下圖所示)。
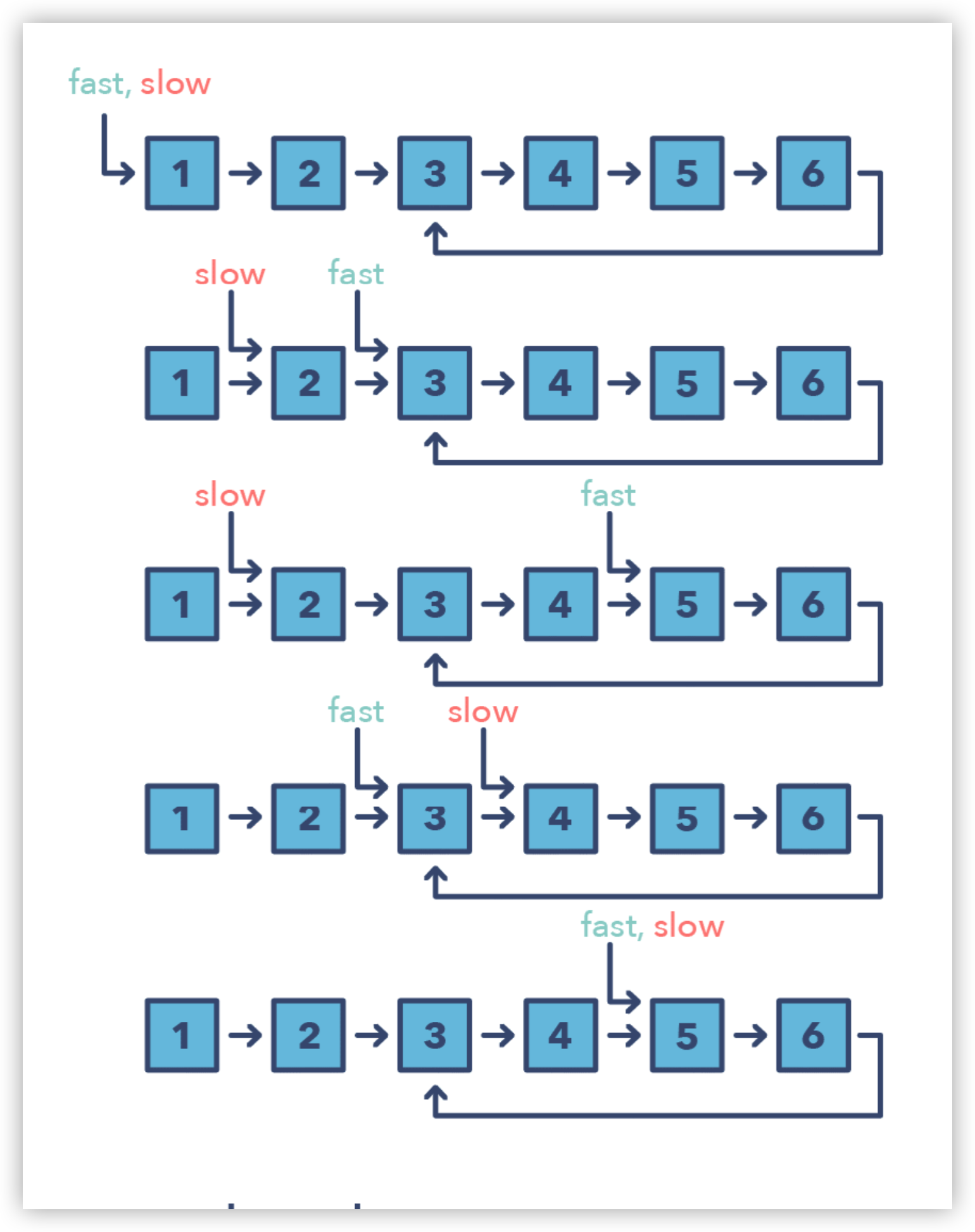
為什么說快指針一定會追上慢指針?,即快慢指針一定會相遇?
這個問題你可以用數學歸納法來思考。首先,由於鏈表是個環,所以相遇的過程可以看作是快指針從后邊追趕慢指針的過程。那么做如下思考:
當快慢兩個指針均落入環中之后【一直往下走兩個指針必定均會落入環中】,落入環中時就一定會是如下情況中的一種,我們歸納討論HINT: 這里我們不考慮當快慢指針均落入環中的那一刻就是在相同位置的情況,那種情況只可能發生在快慢指針的速率是一樣的,那也就不能稱之為快慢指針了,與我們的架設前提不服,因此在此不做討論
1:快指針與慢指針之間差一步。此時繼續往后走,慢指針前進一步,快指針前進兩步,兩者相遇。
2:快指針與慢指針之間差兩步。此時繼續往后走,慢指針前進一步,快指針前進兩步,兩者之間相差一步,轉化為第一種情況。
3:快指針與慢指針之間差N步。此時繼續往后走,慢指針前進一步,快指針前進兩步,兩者之間相差(N+1-2)-> N-1步。因此,此題得證。所以快指針必然與慢指針相遇。
我們簡化為如下的數學模型,假設快慢指針在綠點相遇;假定快指針在環中繞了
P圈在綠點與慢指針相遇,慢指針在環中繞了Q圈在綠點與快指針相遇。我們可以計算出:
快指針走的路程為:
S(快指針路程) = A + (P+1)*B + P*C慢指針走的路程為:
S(慢指針路程) = A + (Q+1)*B + Q*C又因為快指針是慢指針速率的
X倍,因此可得出:
S(快指針路程) = X*S(慢指針路程),即
A + (P+1)*B + P*C = X*{A + (Q+1)*B + Q*C}
P>Q && P,Q均要盡量小[因為是第一次相遇]當快指針的速率為慢指針的速率的兩倍時,即
X = 2
(P-2Q)(B+C) = A+B==>(P-2Q-1)(B+C) + C = A假定環長為D,即
D=B+C,則:
(P-2Q-1)D + C = A且P>Q && P,Q均要盡量小[因為是第一次相遇]當要查找環的起點時,就需要用到上述結論;即當找到相遇節點之后,用一個指針從相遇節點開始往后走,一個節點從頭開始走,當兩者相等時候即為鏈表環的起點。
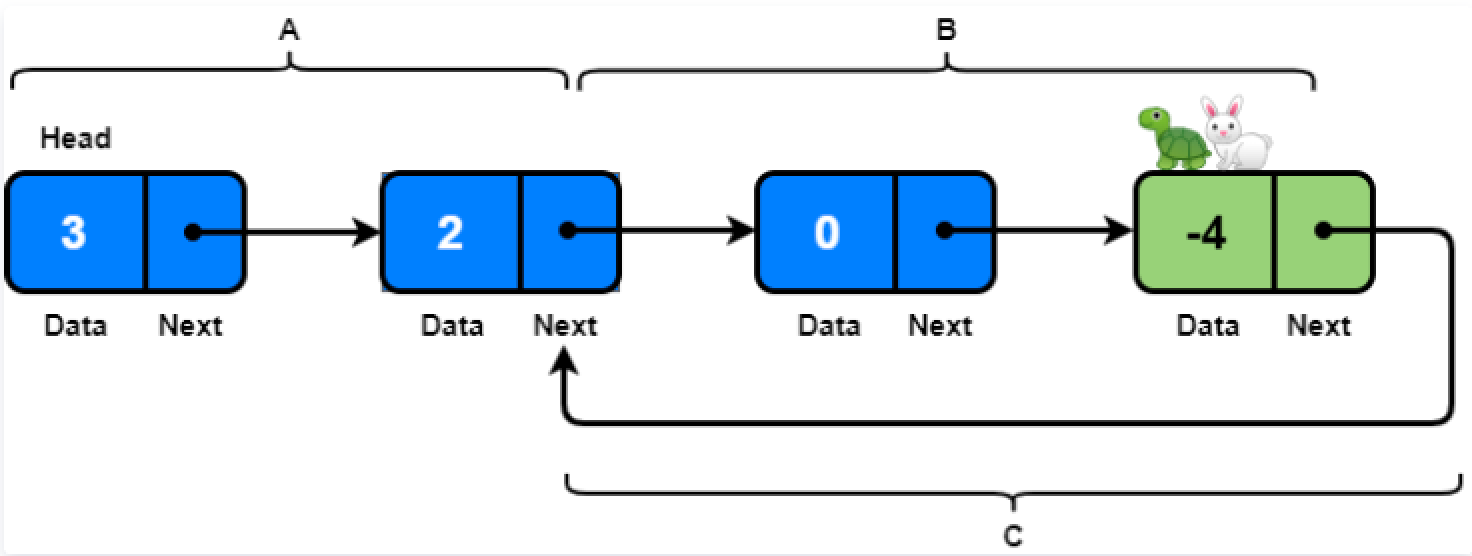
通過上面的結論我們可以輕松解決,判斷鏈表中是否有環以及如何找到對應環的起始點;並且利用快慢指針也能快速找到等分點(最經典的就是二等分點即中點)等問題,可以再刷幾道題實戰一下,雙指針算法基本原理和實踐
歡迎關注
H尋夢人公眾號,更多精彩博文!!!

