記求一個集合的所有子集的三種方法
來源:記求一個集合的所有子集的三種方法-zhyjc6's Blog
前言
今天刷 Leetcode 題目遇到一個求一個無重復元素數組的全部子集,遇到這種題目如果是以前我可能會使用迭代法,首先將一個空數組加入結果集,然后遍歷數組中的元素,對於每個元素,遍歷結果集中的全部子集,向全部子集中加入當前元素得到新的子集,再將這些新的子集加入結果集。但現在我第一想到的不是這個解法,而是回溯法,因為回溯的意義就是找到所有可能的結果。並且回溯法寫起來給人的感覺特別優雅,又易讀易懂,掌握了之后感覺真的很好。
我寫好了之后一遍提交通過,和往常一樣我又來到了討論區,看到了官方題解的一個解法是利用二進制數。我震驚了,這都能扯上關系?看到官方題解有這個方法,那么國際版高贊一定也有這個解法,並且代碼更簡潔,講解更易懂。於是我果然在高贊區看到了。這就是方法三。
我們先看題目描述:
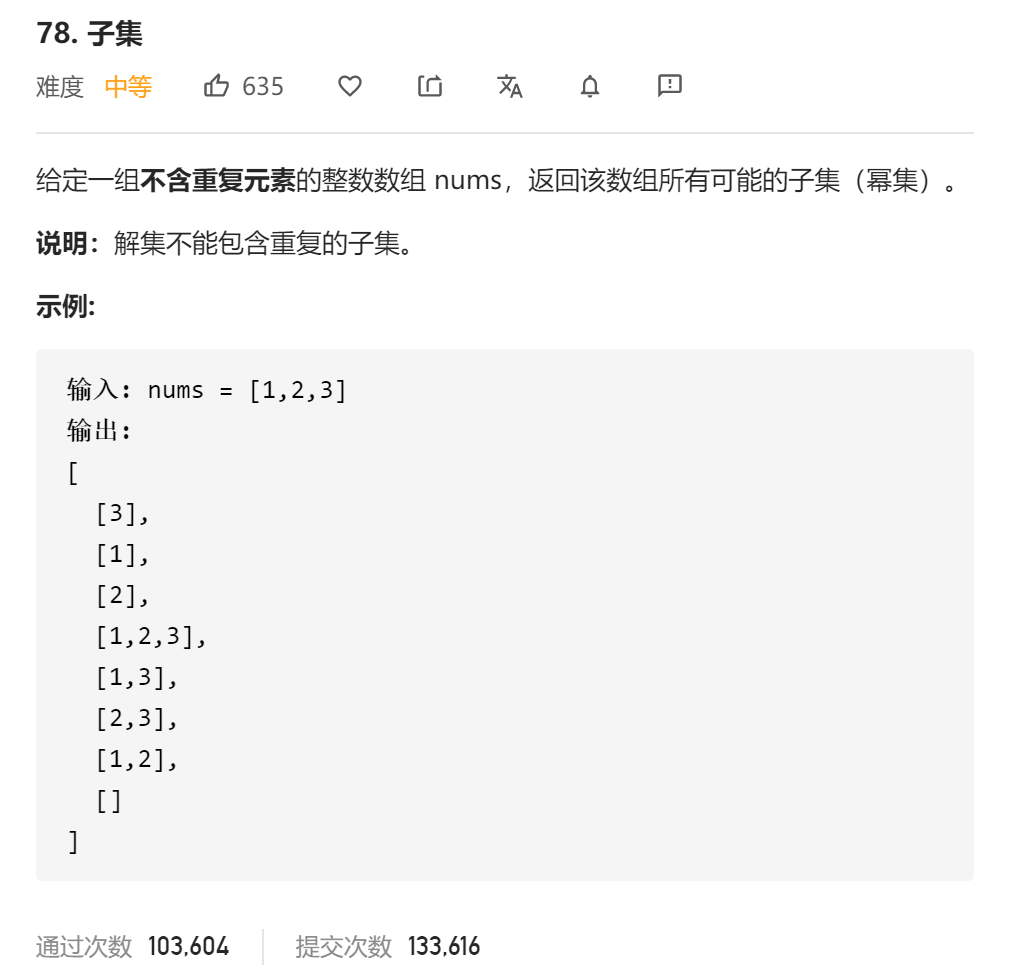
解法一:普通迭代法
思路
- 首先將空集加入結果集中,用作母體產生后面的結果。
- 遍歷數組,對於當前的元素
- 遍歷之前結果集中的子集,將子集加入到結果集中,再將當前元素加入到尾部。
代碼
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums) {
vector<vector<int>> res;
res.push_back({});
for (int num : nums) {
int n = res.size();
for (int i = 0; i < n; ++i) {
res.push_back(res[i]);
res.back().push_back(num);
}
}
return res;
}
};
復雜度
- 時間復雜度:O(N∗2N)O(N∗2N) 。
- 空間復雜度:O(N∗2N)O(N∗2N) 。
方法二:回溯法
思路
定義回溯函數,從start開始遍歷nums數組中的元素,對於當前元素有兩種選擇:
- 選擇加入結果集:那么就從下一個元素開始調用回溯函數
- 不加入結果集:什么也不用做。
代碼
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums) {
backtrack(nums, 0);
return res;
}
private:
vector<vector<int>> res;
vector<int> tmp;
void backtrack(vector<int> &nums, int start) {
res.push_back(tmp);
for (int i = start; i < nums.size(); ++i) {
tmp.push_back(nums[i]);
backtrack(nums, i+1);
tmp.pop_back();
}
}
};
復雜度
- 時間復雜度:O(N∗2N)O(N∗2N) 。
- 空間復雜度:O(N∗2N)O(N∗2N) 。
方法三:二進制法
思路
一個包含 n 個元素的集合的子集數量為 2n2n 。因為每個元素可以選擇選或者不選。深度利用這個規則,我們用二進制數來表示每個元素的選或者不選。那么我們需要一段長為n+1的二進制數。因為我們需要的二進制數范圍為:000…(n個0,表示全部不選,也就是空集) 到 111…(n個1,表示全選,也就是數組本身)。因此我們的limit 就是總的子集數量。
從0遍歷到limit-1,看看當前的二進制數,當前的二進制數中的哪一位為1,就將nums數組中的哪一位加入結果集中。就是這么簡單!!!
代碼
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums) {
int n = nums.size(), limit = 1 << n;
vector<vector<int>> res(limit);
for (int i = 0; i < limit; ++i) {
for (int j = 0; j < n; ++j) {
if ((i >> j) & 1) {
res[i].push_back(nums[j]);
}
}
}
return res;
}
};
復雜度
- 時間復雜度:O(N∗2N)O(N∗2N) 。
- 空間復雜度:O(N∗2N)O(N∗2N) 。
