摘要
如果使用線性表存放 n 個元素時,時間復雜度是 O(n)。如果使用二分法搜索,可以降低時間復雜度,為 O(logn),但是添加和刪除的平均時間復雜度是 O(n)。
使用二叉搜索樹,可以讓添加、刪除、搜索的最壞時間復雜度優化到 O(logn)。
二叉搜索樹,英文為 Binary Search Tree,簡稱 BST。它是二叉樹中的一種,應用的場景也是非常廣泛,其他地方也叫做二叉查找樹、二叉排序樹。主要特點有:
- 任意一個節點的值都大於它左子樹所有節點的值
- 任意一個節點的值都小於它右子樹所有節點的值
- 它的左右子樹也是一棵二叉搜索樹
List 1: 二叉搜索樹
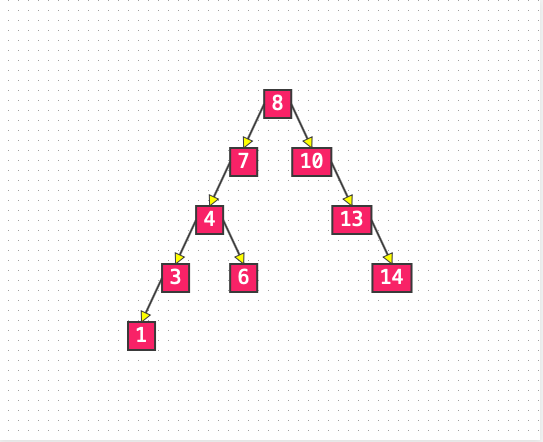
二叉搜索樹能夠大大提高搜索的效率,但是節點中存儲的元素必須具備可比較性,否則搜索效率無從談起。
可比較性
可以比較大小,比如 int、double。這里也可以自己定義比較規則。
但是 null 是不具有可比較性,也就是元素必須不能為 null。
設計接口
在實現二叉搜索樹功能之前,先定義二叉搜索樹的接口,對外使用的接口:
-
元素的數量
int size() -
是否為空
boolean isEmpty() -
清空所有元素
void clear() -
添加元素
void add(E element) -
刪除元素
void remove(E element) -
是否包含某元素
boolean contains(E element)
實現
首先搭建一個類,定義根節點等變量
public class BinarySearchTree<E> implements BinaryTreeInfo {
// 記錄節點的數量
int size = 0;
// 根目錄
Node<E> root;
}
Node 是對節點的定義,感興趣的,可以找找前幾期。
有了 size 和 root 就可以快速實現前三個接口:
int size() {
return size;
}
boolean isEmpty() {
return size == 0;
}
void clear() {
root = null;
size = 0; // size 必須要清空
}
添加元素
添加元素就是創建包含該元素的節點,然后放到合適的位置,比如在原來的二叉搜索樹中添加 12 和 5,得到的結果是:
List2: 添加元素 5 和元素 12

以添加 5 來看,5 是怎么跑到 6 的左子樹中的:
- 根節點是 8(不為 null),5 和 8 比較,結果小於 8,向 8 的左子樹跑;
- 8 的左子樹是 7(不為 null),5 和 7 比較,結果小於 7,向 7 的左子樹跑;
- 7 的左子樹是 4(不為 null),5 和 4 比較,結果大於 4,向 4 的右子樹跑;
- 4 的右子樹是 6(不為 null),5 和 6 比較,結果小於 6,向 6 的左子樹跑;
- 發現 6 的左子樹是 null,確定 6 是 5 的父節點;
- 因為 5 小於 6,那么 5 就放在 6 的左子樹中。
總結出添加的步驟為先找到父節點,然后根據和父節點的比較結果決定放在對應的位置。比較下來,似乎沒有說如果元素相等,怎么辦?這里簡單直接的處理就是覆蓋原來的元素,完成。
代碼實現:
void add(E element) {
// 判斷 element 不能為 null。
elementNotNullCheck(element);
// 是否是添加到第一個元素
if (root == null) {
root = new Node<E>(element, null);
size ++;
return;
}
// 添加到其他位置
Node<E> node = root;
Node<E> parent = null;
int cmp = 0;
while (node != null) {
parent = node;
cmp = compare(element, node.element);
if (cmp > 0) {
node = node.right;
}
else if (cmp < 0) {
node = node.left;
}
else {
// 元素相等,就直接替換,完成
node.element = element;
return;
}
}
// 注意是插入 parent 的 left 或者 right
Node<E> newNode = new Node<>(element, parent);
if (cmp > 0) {
parent.right = newNode;
}
else if (cmp < 0) {
parent.left = newNode;
}
else {
}
}
compare 是自定義的比較方法,感興趣可以看最后的補充部分。
是否包含某元素
趁熱打鐵,可以使用 compare 方法可以實現根據元素內容獲取節點的方法:
public Node<E> node(E element) {
if (element == null) { return null; }
Node<E> node = root;
while (node != null) {
int cmp = compare(element, node.element);
if (cmp > 0) {
node = node.right;
}
else if (cmp < 0) {
node = node.left;
}
else {
return node;
}
}
return null;
}
那么是否包含某個元素也就可以轉換為判斷該元素獲取到的節點是否為 null:
boolean contains(E element) {
return node(element) != null;
}
刪除元素
刪除元素也是可以轉換為刪除節點,二叉搜索樹刪除節點有3種情況要考慮處理:
- 節點是葉子節點
- 節點是度為 1 的節點
- 節點是度為 2 的節點
度是什么?
度是節點中子節點的個數,二叉樹中每個節點的度最小為 0,最大為 2。
葉子節點就是度為 0 的節點
節點是葉子節點
若刪除的節點是葉子節點,處理上比較簡單,就是將這個葉子節點設置為 null。這里只需要考慮這個節點是根節點的情況,遇到這個情況就需要將 root = null 處理。
節點是度為 1 的節點
若刪除的節點是度為 1 的節點,那么就可以用這個節點的子節點來替代它的位置。當然也要考慮若這個節點是根節點,那么就需要將 root 指向它的子節點。
List3: 刪除元素 4 和元素 13

節點的度為 2 的節點
若刪除的節點是度為 2 的節點,那么就需要先找到這個節點的前驅或者后繼節點,覆蓋該節點,然后刪除再刪除對應的前驅或者后繼。(前驅或者后繼,詳細看最底部補充部分)
這樣做是為了保持繼續保持節點的左子樹都比節點小,節點的右子樹都比節點大的性質。
List4: 刪除度為 2 的元素 8

實現
整理梳理完刪除節點的三種情況后,可以看到度為 2 的節點是在更換前驅或者后繼之后,再次回到了處理度為 0 或者 1 的情況下,接下來的處理,在最后去判斷是否是根節點,那么代碼實現邏輯上就可以先處理度是 2 的節點,然后處理度為 0 或者 1 的節點,在最后判斷節點是否是 root 節點。
void remove(Node<E> node) {
if (node == null) { return; }
size --;
// 度為 2 的節點
if (node.isHaveTowChildren()) {
// 找到后繼節點
Node<E> s = successor(node);
// 后繼節點的值賦值給 node
node.element = s.element;
// s 節點給 node 節點,為刪除 node 節點准備
node = s;
}
// 節點的度非 0 即 1
Node<E> replaceNode = node.left != null ? node.left : node.right;
// 度為 1 的節點
if (replaceNode != null) {
replaceNode.parent = node.parent;
// root 節點
if (node.parent == null) {
root = replaceNode;
}
else if (node == node.parent.left) {
node.parent.left = replaceNode;
}
else {
node.parent.right = replaceNode;
}
}
else if (node.parent == null) { // 度為 0 的節點,且是 root
root = null;
}
else { // node 是葉子節點,但不是 root
if (node == node.parent.left) {
node.parent.left = null;
}
else {
node.parent.right = null;
}
}
}
補充
compare 方法
這里使用 JAVA 系統中的 Comparator 類,先創建對象,設置 E 類型,保證 E 類型的數據遵守比較協議:
private Comparator<E> comparator;
之后實現比較方法:
private int compare(E e1, E e2) {
if (comparator == null) {
return ((Comparable<E>)e1).compareTo(e2);
}
return comparator.compare(e1, e2);
}
前驅節點和后繼節點
前驅節點是中序遍歷時的前一個節點,也是二叉搜索樹中,比它小的前一個節點。
即為 node.left.right.right...,但是當 node.left == null 時,為 node 的父節點(比如元素 5 的前驅為元素 4)。
后繼節點是中序遍歷時的后一個節點,也是二叉搜索樹中,比它大的后一個節點。
即為 node.right.left.left...,但是當 node.right == null 時,為 node 的父節點(比如元素 5 的后繼為元素 6)。
List 6: 前驅和后繼
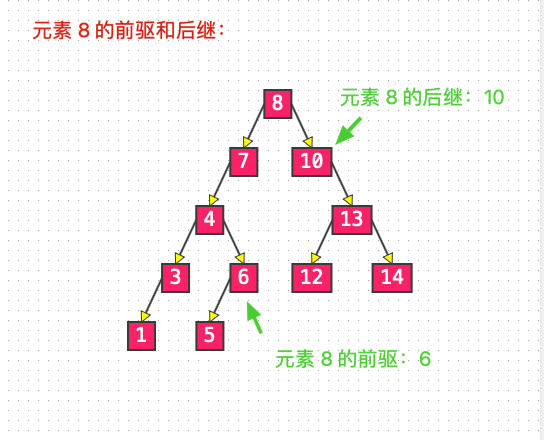
predecessor 獲取前驅節點
要留意代碼中的終止條件
public Node<E> predecessor(Node<E> node) {
if (node == null) return null;
// 前驅節點在左子樹中
Node<E> p = node.left;
if (p != null) {
while (p.right != null) {
p = p.right;
}
return p;
}
while (node.parent != null && node == node.parent.left) {
// 前驅節點在父節點中,並 node 在 parent 的右子樹中
node = node.parent;
}
// node.parent == null
// node == node.parent.right
return node.parent;
}
successor 獲取后繼節點
要留意代碼中的終止條件
public Node<E> successor(Node<E> node) {
if (node == null) return null;
// 前驅節點在右子樹中
Node<E> p = node.right;
if (p != null) {
while (p.left != null) {
p = p.left;
}
return p;
}
while (node.parent != null && node == node.parent.right) {
// 前驅節點在父節點中,並 node 在 parent 的左子樹中
node = node.parent;
}
// node.parent == null(根節點)
// node == node.parent.right
return node.parent;
}
