今天給大家講一下卷積神經網絡，主要包括四個部分：卷積神經網絡的歷史、全連接層、卷積層和池化層。
CNN的英文全稱是Convolutional Neural Network，雛形是LeCun在1998年發明的LeNet網絡結構。
LeNet網絡架構
那么到底什么是神經網絡呢？應該說只要帶有卷積層的就可以被叫做卷積神經網絡。
神經網絡的發展歷史
1986年：Rumelhart和Hinton等人提出了反向傳播（Back Propagation）算法。
1998年：LeCun基於BP神經網絡訓練了LeNet網絡，標志着CNN的真正面世。
2006年：Hinton在他們的Science Paper中首次提出了Deep Learning的概念。
2012年：其實在2006年Hinton提出深度神經網絡之后，受到了很多的質疑，但是在2012年Hinton的學生Alex Krizhevsky在寢室用GPU死磕了一個Deep Learning模型，一舉拿下了計算機視覺TOP領域ILSVRC 2012的冠軍，在百萬量級的ImageNet數據集合上，效果大幅度的超過了傳統的方法，准確率從70%提升到80%。
全連接層
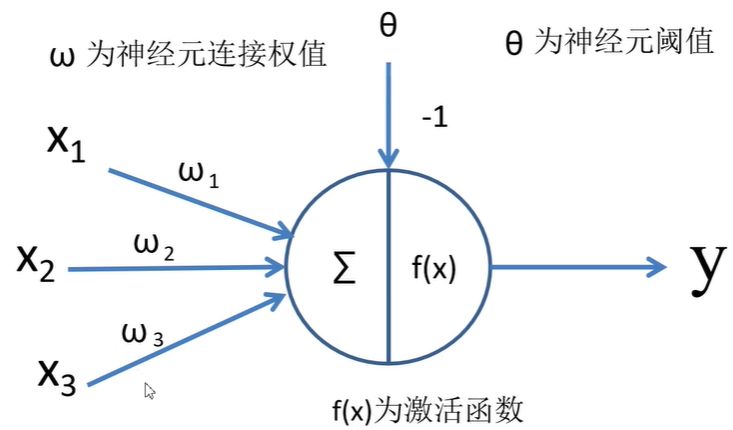其實全連接層就是模仿大腦的神經元結構，我們可以看到：
輸出值 = 輸入值x經過加權w之后累加的結果再經過激勵函數。形式化為：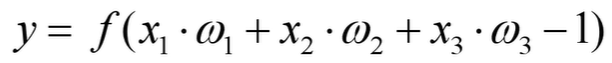
那么我們將神經元按列進行排列，列與列之間進行全連接，就得到了一個BP神經網絡。
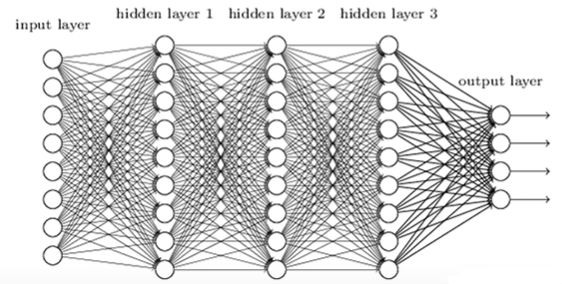BP神經網絡算法包括信號的前向傳播和誤差的反向傳播兩個過程。即計算誤差輸出時按從輸入到輸出的方向進行，而調整權值和閾值則從輸出到輸入的方向進行。
下面我們來看一個實例來了解一下BP神經網絡。
實例：利用BP神經網絡進行數字識別
我們拿到一張圖片，例如上邊第一張圖所示拿到的是0，這張圖是由若干像素組成，每個像素有RGB三個通道，然后經過灰度化后變成第二張圖片，然后將灰度化后的圖片進行二值化得到第三張圖片。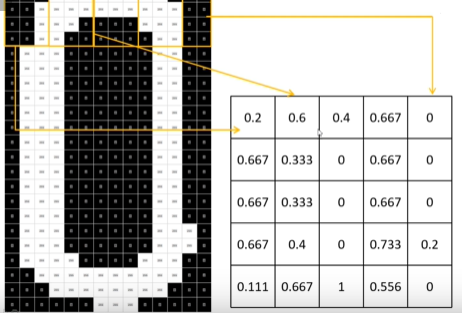
之后我們對圖片進行概率處理，例如第一個框中白色塊/全部塊 = 0.2，經過相應的策略處理之后第一個數值為0.2。以此類推，可以得到上圖右邊的矩陣。
然后我們對這個矩陣進行維度變換和處理，將其變為1*n的行向量，這樣處理之后的形式可以使得神經網絡更好的輸入處理。
我們知道神經網絡如何輸入了，那么最后應該輸出什么才可以更好的辨別數字呢？One-Hot編碼！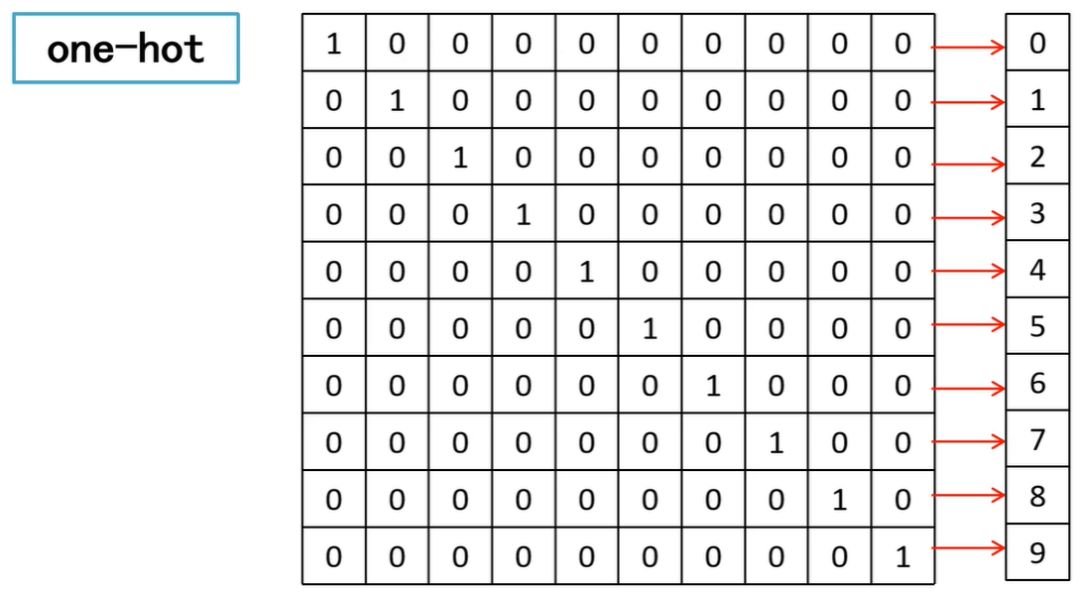
也就是說，每個數字都對應一個編碼，如果輸入1000000000，則判定為數字0，以此類推。
既然有了輸入，也有了輸出，我們就可以通過神經網絡對其進行訓練了。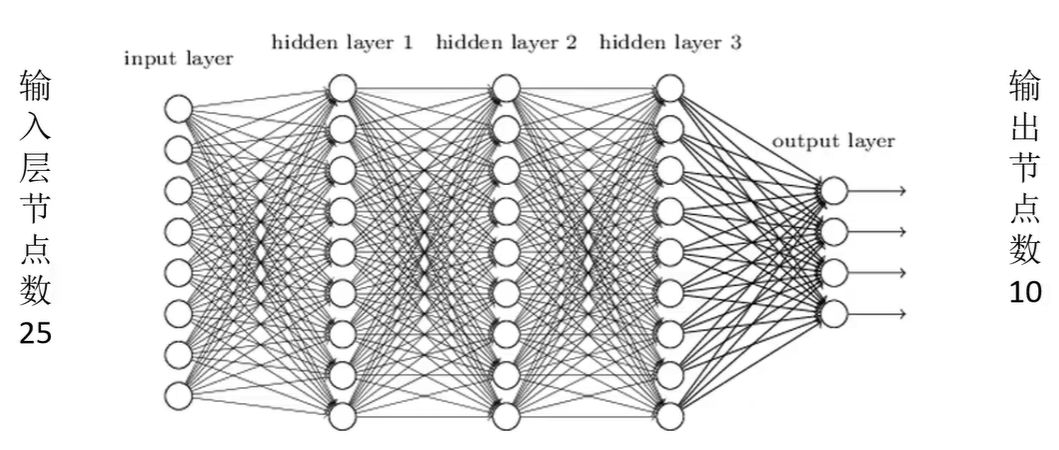
首先將輸入層的神經元數設置為25個節點，將輸出層設置為10個節點，將上邊1*n的向量輸入到BP神經網絡中，然后經過隱藏層最后到輸出層onehot編碼，輸出層通過softmax激活函數可以得到每個數字出現的概率，即可識別數字。
卷積層
到底什么是卷積層？之前的文章中講過了，有興趣的可以直接查看。
漫畫：卷積神經網絡中的卷積核到底是什么？
漫畫：卷積神經網絡為什么適合處理圖片數據？
干貨 | 如何入手卷積神經網絡
在卷積層的講解中，想問大家一個問題，卷積核如果越界了應該如何處理？例如下面這樣：
假設用這么一個矩陣，我們使用3*3的滑動窗口，步長為2，則手機號購買地圖出現下面這種情況應該如何處理？
我們可以對其進行使用Padding對其進行補0處理，如下所示：
在卷積操作過程中，矩陣經過卷積操作之后大小由下面幾個因數決定：
- 輸入圖像大小W*W
- Filter大小F*F
- 步長S
- padding的像素數P
經過卷積后的矩陣尺寸大小是有一個規律的，那么給大家一個通用的公式：N=(W-F+2P)/S+1
池化層
為什么要存在池化層？因為當前的輸入數據太大，有很多冗余信息，那么我們就要想辦法對圖像矩陣進行下采樣，對特征圖進行稀疏處理，減少數據運算量。下面通過MaxPooling下采樣來給大家看一下到底什么是池化層。
上圖中紅色部分的值為1 1 5 6，我們使用的是MaxPooling，所以取最大值，則右圖中紅色部分為max(1,1,5,6)=6，以此類推，即可得到下采樣結果。
類似於最大下采樣，同樣也有平均下采樣層，如下圖所示：
為了大家更好的理解和使用池化層，我總結了池化層的三個特點：
- 沒有訓練參數
- 只會改變特征矩陣的w和h，不改變channel
- 一般pool size和卷積核的stride相同
今天講的是卷積神經網絡的整體架構基礎，包括神經網絡的發展歷史、全連接層、卷積層和池化層，大家有什么見解或者想法都可以在下面留言哦~