【算法學習筆記】博弈論淺析之游戲類

一、取走游戲

​ 首先，我們介紹一下組合游戲。組合游戲是一種兩個人參與的游戲，參與者擁有完整的（有關游戲的）信息，沒有任何意外產生的操作(即保證無意外性)，並且游戲擁有一個輸贏的結果。這樣的游戲是由一系列的位置，包括一個起始位置，和哪個參與者進行下一步所組成、決定的。游戲在參與者的選擇中從一步移向下一步，最終達到某個終點位置。這樣的一個終點位置意味着沒有任何下一步移動存在的可能。之后，其中一名游戲者被判定為勝利，另一名則為失敗。
​ 這個理論可以被分為兩個部分：公平游戲，游戲中對於兩名參與者所被給定的任意一個位置，都能夠到達其他所有的位置(強調兩名參與者相同機會)。非公平游戲，則是被給定的不同位置對於兩名參與者有着不同的機會，例如國際象棋。
在第一部分我們將只討論有關於公平游戲的部分，下面講一個簡單的例子。

簡單的取走游戲

我們來分析這樣一個游戲，下面介紹下游戲規則：

1. 兩名參與者，我們成為 A和B (懶得打羅馬數字1和2)
2. 桌上有 \(21\) 根火柴。
3. 每次只能從火柴堆中拿下 \(1、2、3\) 根火柴
4. 參與者輪流拿火柴，A先手
5. 最后一個拿走剩下所有火柴的人贏

現在知道游戲規則了，我們就嘗試着來分析這個游戲。想一想，其中一名參與者一定能夠在游戲中勝利嗎？我們要先手還是要后手？有什么很好的策略嗎？

下面，我們將從后往前分析這個游戲，即從游戲即將結束的部分開始。這種方法被稱為倒退歸納。

• 假設只剩下1、2、3根火柴，顯然拿走剩下這幾根火柴就贏了。
• 假設剩下4根火柴，那么這時候輪到拿火柴的人肯定輸，因為怎么拿都會剩下，然后他的對手拿掉剩下的火柴就贏了。所以4根火柴的情況是先手必敗。
• 那么，我們遞推到5、6、7根火柴，顯然，只要拿剩下4根，那么就讓對手陷入先手必敗狀態。5、6、7根火柴便是先手必勝狀態。那么若剩下8根火柴，這時候輪到的參與者肯定輸，因為你只能拿到剩下5、6、7根火柴，讓對手進入先手必勝的狀態。
• 所以，我們發現，0，4，8，12，16„根火柴是一個目標狀態。我們要爭取使自己進入這個狀態。現在我們便能分析21根火柴的游戲了，既然21不被4整除，第一個移動火柴的人（即先手者，參與者A）肯定贏。唯一的策略便是拿走一根火柴，剩下20根讓對手絕望去。

究竟什么是組合游戲？

現在我們將組合游戲的概念定義得更准確一些。

組合游戲是一個滿足下列情況的游戲：

1. 兩名參與者 （經典 Alice 和 Bob）
2. 游戲中有一系列通常是有限個數的可能的情況或位置。
3. 游戲規則是對兩名參與者同時有效的，並且每個位置向另一個位置移動都是合法的。如果規則對於兩名參與者沒有區別，也就是說兩名參與者遇上同樣的情況時，有着相同的選擇個數和選擇情況，那么這個游戲被稱為一個公平游戲。否則，稱為不公平游戲。
4. 參與者交替進行游戲
5. 游戲結束時，意味着到達一個終點。一般規則下，最后一次操作的人獲勝，但在逆規則下，最后一次操作的人失敗。這樣的一個終點位置意味着沒有任何下一步移動存在的可能。使游戲到達終點的人為勝者，另一個為敗者。如果游戲不能結束，那么稱為平局。然而，我們幾乎總是添加一個結束位置。這樣就避免了平局的可能性。
6. 游戲在有限步數內會結束，無論怎么進行。 我想很有必要提醒在這個定義中省略了什么：沒有隨機移動，比如擲骰子；一個組合游戲是一個擁有完整信息的游戲：同時移動和隱藏移動是不允許的；沒有平局。

P 位置和 N 位置（先手必敗狀態和先手必勝狀態)

回到剛剛說的取走游戲中，我們發現 $0，4，8，12，16... $ 是一個對於前一個操作的參與者勝利的位置(Previous Player)，而 \(1,2,3,5,6,7,9,10,11\) 是對現在或者說是下一個操作的參與者勝利的位置(Next Player or Now Player). 前者則稱為P位置，后者稱為N位置。(作者注：在下文中，P位置也會被稱為先手必敗狀態，N位置也會被稱為先手必勝狀態)。在一個公平游戲中，我們可以找到規律，哪一個是先手必勝狀態，哪一個是先手必敗狀態，只要從結束狀態開始通過下列的操作進行倒推即可。

1. 每個結束狀態都是先手必敗狀態。
2. 如果當前狀態能夠轉移到先手必敗狀態(P位置)的狀態，則這個狀態為先手必勝狀態（N位置）。
3. 如果當前狀態所能轉移到的所有狀態都是先手必勝狀態(N位置)，那么這個狀態為先手必敗態（P位置）。

而這樣分析之后，很明顯，任意一個處於P位置的人肯定會輸，因為他只能轉移到N位置。而處於N位置的人，只要轉移到P位置就可以贏了。
從上面的推導，顯然地，我們會發現對於N位置和P位置有一些性質，這些性質的前提是，這是公平游戲，且有終點。

1. 終點是P位置。
2. 所有P位置能轉移到的都是N位置
3. N位置至少能轉移到一個P位置

減法游戲

​ 現在我們把上面所提到的簡單取走游戲一般化。設 \(S\) 表示一個正整數的集合，那么以S為減法集的減法游戲就是像這么玩的：有一堆 \(n\) 根火柴，每次像簡單取走游戲一樣拿去火柴，但是拿去的火柴數必須在減法集中。其他規則同減法游戲。
​ 那么，簡單的取走游戲就是一個 \(S=\{1,2,3\}\) 的減法游戲。現在為了更好地說明，我們來討論一個 \(S=\{1,3,4\}\) 的減法游戲。首先，(個數)0是終點，為 \(P\) 位置。而 \(1,3,4\) 則為 \(N\) 位置，因為可以轉移到0這個 \(P\) 位置。2是 \(P\) 位置，因為2只能轉移到1，而1為 \(N\) 位置。5,6是 \(N\) 位置，因為可以轉移到2。7是P位置，因為7能轉移到的是3,4,6，都是N位置。
按着這樣子遞推下去，我們會發現

\[P=\{0,2,7,9,14,16,...\} \\ N=\{1,3,4,5,6,8,10,11,12,13,15,...\} \]

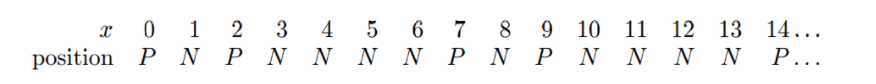
我們會發現，\(PNPNNNN\) 是一個長度為7的循環節。現在，如果是 \(100\) 根火柴，先手贏還是后手贏？我們發現，\(100\ mod\ 7 = 2\)，對應循環節，\(2\) 是 \(P\) 位置，所以 \(100\) 根火柴是先手必敗狀態，后手肯定贏。

現在，請你嘗試着分析一個\(S=\{1,2,3,4,5,6\}\) 的減法游戲，並搞清楚 \(10000\) 根火柴的話，先手贏還是后手贏？

《Game Theory》中有對應練習，請讀者自行查找

二、Nim 游戲

游戲規則

​ Nim游戲是最有名的取走游戲。有三堆火柴，分別有 \(x_1,x_2,x_3\) 根火柴(比如 \(5,7,9\) )。兩個人輪流進行操作，每次只能取走一堆火柴中任意數量的火柴，不能同時對多堆進行操作。和取走游戲一樣，拿走剩下所有火柴的人獲勝。

初步分析

​ 我們用(\(x_1,x_2,x_3\))表示對應三堆分別有 \(x_1,x_2,x_3\) 根火柴的狀態。
首先，只有一個終點，(\(0,0,0\))，為 \(P\) 位置。因為可以拿走一堆中任意根數的火柴，所以 \((x,0,0)，(0,x,0)，(0,0,x) (x>0)\) 為 \(N\) 位置。但是推廣到 \((x,y,0)\) ，也就是有 \(2\) 堆火柴不為空的時候，還勉強可以計算，但到了\((x,y,z)\) ，我們會發現推導起來無比糾結。所以，我們這里要引入另外一個東西。

Nim 和

首先，我們定義 Nim和 為兩個數或多個數在二進制下的異或和(異或和部分不作展開介紹，請不懂的讀者自行找資料)。我們定義 “\(⊕\)” 為Nim和的運算符號。例如，如果 \(x\) 與 \(y\) 的 Nim和 是z，那么我們表示為 \(x⊕y=z\) 。

然后，引入波頓定理。

波頓定理：對 \(n\) 堆火柴 (\(x_1,x_2,x_3,...,x_n\) )，若 \(x_1⊕x_2⊕...⊕x_n = 0\) ，則這個狀態為 \(P\) 位置，否則為 \(N\) 位置。

舉個例子，對於 \((x_1,x_2,x_3)=(13,12,8)\)，計算它的 Nim和：

\[13 = 1011_2 \\12=1100_2 \\\ 8=1000_2 \\--------\\ Nim - sum =1001_2=9 \]

Nim和不是0，根據波頓定理，這是一個N位置。那存在能找到移動到P位置的方法嗎？

根據Nim和的定義，我們發現，只要把每一列的 \(1\) 改為偶數個數就可以了。那么我們把第一堆火柴拿掉 \(9\) 根，這樣子狀態變為 \((4,12,8)\) ，而它的 Nim和：

\[4 = 100_2\\ 12=1100_2\\ 8=1000_2\\ ------\\ Nim - sum = 0000_2 = 0 \]

根據波頓定理，這是一個P位置。我們還可以找到另一種方法，也就是從第二對堆的 \(12\) 根火柴中拿掉 \(7\) 根，剩下 \(5\) 根，同樣可以得到Nim和為0。

波頓定理的證明

波頓定理的證明參考於：Here

簡單證明：

• 當 \(a\) 不全為 \(0\) 時, 任意一個 \(res!=0\) 的局面, 先手可以通過一定的操作讓后手面對 \(res=0\) 的局面。
• 對於任意一個 \(res=0\) 的局面, 先手無法通過任何操作讓后手面對 \(res=0\) 的局面。
• 得出結論, 當 \(res=0\) 時先手必敗, 反之必勝。

詳細證明：

假設現在分析 \(S(x_1,x_2,x_3,...,x_n)\) 這個狀態

1. 對於終點 \((0,0,0,...,0)\)，顯然 \(0⊕0⊕0⊕...⊕0=0\) ，而終點為 \(P\) 位置，成立。

2. $x_1⊕x_2⊕...⊕x_n ≠0 $

   由 \(N、P\) 位置的定義，我們知道每個 \(N\) 位置都能移動到至少一個 \(P\) 位置。下面我們來研究如何構造這樣一個移動。類似上面兩圖的計算，我們將 Nim和看成一個豎的加法。我們找到第一列有奇數個“1”的那一列，並把任意在這一列上的“1”換成0，然后在這個數后面繼續找，發現某一列的“1”的個數為奇數時，我們只要把這一列的數取反就好，即“1”變“0”，“0”變“1”。這樣得出來的這個數，就是你要拿掉火柴后剩下的數。顯然的，這樣的一個數是肯定找得到的。也就是說，可以從該位置找到至少一個達到Nim和為0的方法，符合N位置的性質。

3. $x_1⊕x_2⊕...⊕x_n =0 \( 由\)N、P$位置的定義，我們知道每個 \(P\) 位置所能移動到的都是 \(N\) 位置。假設我們這時候把 \(x_1\) 上拿掉火柴，使它變成\(x_1’\) 根(\(x_1’<x_1\))。因為 \(x_1⊕x_2⊕...⊕x_n =0\) ，所以 \(x_1’⊕x_2⊕...⊕x_n ≠0\) ，也就是所能得到的都是 \(N\) 位置，符合 \(P\) 位置的性質。

反 Nim游戲

反Nim游戲是在逆規則下進行的Nim游戲，也就是最后操作的人失敗。

在逆規則下，還能找到對於任意狀態的必勝解法嗎？一開始想覺得好像有點麻煩，但仔細想想，其實是可以比較簡單地解決的。

先手勝當且僅當

1. 所有堆石子數都為1且游戲的SG值為0
2. 存在某堆石子數大於1且游戲的SG值不為0

證明：

1. 若所有堆石子數都為1且SG值為0，則共有偶數堆石子，故先手勝。

1）只有一堆石子數大於1時，我們總可以對該堆石子操作，使操作后石子堆數為奇數且所有堆得石子數均為1。 II

2）有超過一堆石子數大於1時，先手將SG值變為0即可，且總還存在某堆石子數大於1。

(摘自: http://hzwer.com/1950.html) 

對於反Nim游戲，其實還算比較簡單的。但，是不是對於其它的游戲，它們在逆規則下也是可以這樣去簡單分析呢？嗯，實際上對於一些游戲是可以的，但是對大部分游戲來說，就算它們在正常規則下很容易分析，但在逆規則下會變得十分復雜，比如在后文中介紹的 Kayles and Dawson’s chess(第3章，第4部分)。

三、圖論游戲

​ 在這里，我們將用有向圖來表示之前所講的幾種游戲，我們用點來表示游戲中的狀態，而用邊來表示一個狀態能到達另一個狀態。接着我們會定義一個叫做 \(SG\) 函數的東西，而在第四部分中我們將介紹 \(SG\) 定理，它可以更方便我們去確定\(N、P\) 位置。

圖的定義

一個有向圖 \(G\)，是一對 \((X,F)\) ，其中X為一個非空點集(位置)，而 \(F\) 是表示對於任意 \(x∈X,F(x)∈X\)，表示可以將 \(x\) 移動到的位置的集合，我們稱 \(F(x)\) 為 \(x\) 的后繼。顯然，如果 \(F(x)\) 為空集，那么 \(x\) 為終點。

游戲規則

兩個人在 \(G=(X,F)\) 的圖上進行圖論游戲，以 \(x_0\) 為起點，雙方輪流操作。在位置 \(x\) ，操作者可以將 \(x\) 移動到任意\(x_t∈F(x)\) 。移動到終點的人為勝利者。如果按着這個規則，可能會出現這個圖論游戲可以無限制地進行的可能，所以《Game Theory》中給出如下定義：

To avoid this possibility and a few other problems, we first restrict attention to graphs that have the property that no matter what starting point x0 is used, there is a number n, possibly depending on x0, such that every path from x0 has length less than or equal to n. (A path is a sequence \(x_0, x_1, x_2,...,x_m\) such that \(x_i ∈ F(x_{i−1})\) for all \(i = 1,...,m\), where m is the length of the path.) Such graphs are called progressively bounded. If X itself is finite, this merely means that there are no cycles. (A cycle is a path, \(x_0, x_1,...,x_m\), with \(x_0 = x_m\) and distinct vertices \(x_0, x_1,...,x_{m−1}, m ≥ 3\))

這里就是給出了一個圖的限制：圖的大小無限，但是從圖上任意一個點，一定存在一個正整數 \(n\)，使從該點開始到終點的所有路徑長度都不大於 \(n\)。

游戲分析

為了方便講解，我們拿第一部分中的 \(S=\{1,2,3\}\) 的減法游戲進行分析。剩余的火柴數為點，那么 \(n\) 就是起點。因為 \(0\) 終點，沒有后繼，所以 \(F(0)=\) ∅ 。同樣的，我們會得到 \(F(1) = \{0\}，F(2) = \{0,1\}\)，並且對於 \(2 ≤ k ≤ n, F(k) = \{k−3, k−2, k−1\}\) 。對於10根火柴的情況，我們可以得到下圖。

SG 函數 （The Sprague-Grundy Function）

定義：\(g(x) = min\{n \ge 0: n \not = g(y) | y \in F(x)\}\)

用文字來表示，就是不存在於x的所有后繼的SG函數值(后簡稱SG值)中的最小值。比如：\(F(4)=\{1,2,3\}，g(1)=0,g(2)=1,g(3)=4\)，那么 \(g(4)=3\)。再比如同樣的\(F(4)，g(1)=1,g(2)=2,g(3)=3\), 那么 \(g(4)=0\)。
我們將定義中的式子簡寫為：

\[g(x) = mex\{g(y) : y ∈ F(x)\}  \]

我們會發現，求某個 \(x\)，必須遞歸地去求出來，所以一般是用遞推實現的。顯然， F(0)=∅，所以 \(g(0)=0\)，而對於所有后繼只有終點的，\(g(x)=1\)。我們后面將用這樣的方式進行推導得出 \(SG\) 值。
如果我們知道了\(SG\)值，對一個圖論游戲的分析便變得很簡單了。如果 \(g(x)=0\) ，顯然這是個P位置，如果 \(g(x)≠0\)，顯然這是個 \(N\) 位置。說明如下：

1. 如果x為終點，沒有后繼，\(g(0)=0\)
2. \(g(x)=0\)時，因為 \(g(x)=0\)，所以對於所有 \(y∈F(x) ，g(y)≠0\) ，也就是到達的都是N位置。
3. \(g(x)≠0\)時，必然存在 \(y∈F(x) ，g(y)=0\)，即可以到達一個P位置。

當然，SG函數值肯定包含不只這些信息，更多的應用我們將在第四部分的SG定理中看到，它可以解決多個圖同時存在的圖論游戲的問題。

例子

我們將用下圖來介紹 \(SG\) 函數的推導過程。其實很簡單，如定義中一樣，只要找到一個點的所有后繼，然后找到不在它們后繼的 \(SG\) 值之中的值即可。在圖中，我們可以發現有4個終點，位於圖的左側和底部，這四個點的SG值就為0。接着我們會發現只有1個點的后繼已經全部確定了，就是a點，它的SG值為1。現在b和c的后繼的SG值也已全部確定，所以b,c的SG值分別確定出來。這樣不斷重復這個過程，知道將整張圖的SG值都確定下來。

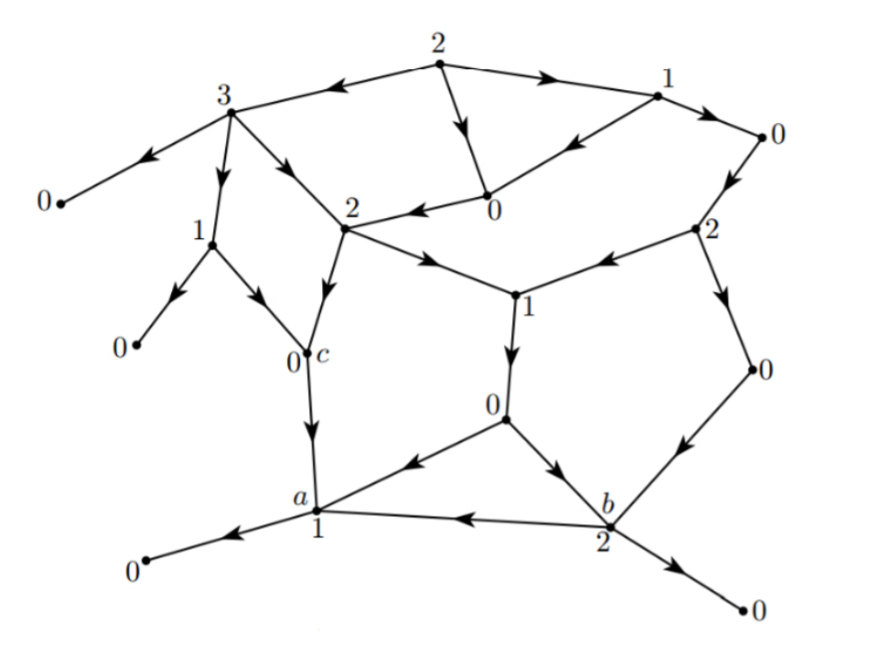
對於之前提到的 \(S=\{1,2,3\}\) 的減法游戲，它對應的SG函數是怎樣的呢？終點 \(0\)，\(g(0)=0\)。狀態1只能移動到終點 \(0\)，所以 \(g(1)=1\) 。狀態2可以移動到 \(0,1\) ，所以 \(g(2)=2\) 。同理得到 \(g(3)=3\) 。對於狀態4，它能移動到 \(1,2,3\) ,分別對應\(g(x)=\{1,2,3\}\)，所以 \(g(4)=0\)。繼續重復下去，我們會得到：

觀察后發現，\(g(x)=0\) 當且僅當 \(x\ mod\ 4=0\)
下面提到一種叫做至少拿一半的游戲。同樣是火柴堆，但是每次你至少要拿走一半。和上面一樣，我們會得出它的SG函數：

觀察后，會發現 \(g(x)=min\{k|2k > x\}\)
然后仔細一想，是不是腦子進水了才去算SG值，至少拿一半，我全部拿掉不就得了...但是，在下一部分中我們會發現計算SG值是很有必要的，配合這 Nim和 來使用，可以很方便地處理多堆火柴的情況。

四、組合游戲的和

定義

給定多個組合游戲，那么你可以將這幾個組合游戲合成一個新的游戲。游戲規則如下：

1. 每個游戲給定一個初始狀態。
2. 雙方輪流操作
3. 對於一次操作，參與者可以對其中一個組合游戲進行符合這個游戲的規則的合法操作，而其他游戲保持原狀態。
4. 游戲進行直至所有組合游戲都到達終點狀態，即操作者無法繼續進行為止。
5. 最后一名操作者獲勝。

圖論游戲的和

​ 假定我們有多個滿足第三部分中限制的圖 \(G_1=(X_1,F_1),G_2=(X_2,F_2),...,G_n=(X_n,F_n)\) 。我們可以把這多個圖組成一個新的游戲 \(G=(X,F)\),稱之為圖 \(G_1,G_2,...,G_n\) 的和，表示為 \(G=G_1+G_2+...+G_n\)。點集X是多個點集的笛卡爾乘積，\(X=X_1*X_2*...*X_n\)，即集合中的點為 \(\{x_1,x_2,...,x_n\}\) ,其中對於任意 \(i∈[1,n], x_i∈X_i\) 。同時對於一個點，其后繼 \(F(x)\) 定義為

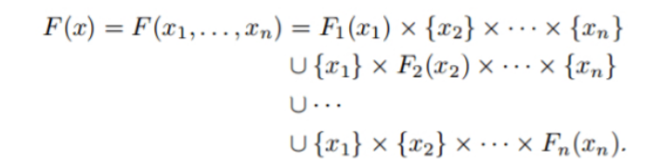
​ 因此，從 \(x=\{x_1,x_2,...,x_n\}\) 開始的一步移動，就是將其中任意一個 \(x_i\) 移向 \(F(x_i)\)。這樣的游戲成為圖論游戲的和。
​ 如果每個子游戲都滿足第三部分中對圖的限制，那么所得到的母游戲也符合那個限制。其移動步數的最大值顯然就是所有子游戲移動步數最大值的和。

SG 定理

接下來介紹的 \(SG\) 可以很方便地求出對於圖論游戲的和中的 \(SG\)值。這需要用到之前所提到的Nim和。
\(SG\) 定理：母游戲的SG值等於其各個子游戲的SG值的Nim和。

應用

SG定理在大多數組合游戲的和中可以用於求出其SG函數值，而更多的時候，我們是通過SG定理暴力求出SG函數值之后去尋找規律，減少麻煩。在《Game Theory》中有講到很多實用的例子，作者由於時間以及能力問題暫未能夠完全理解，在此不進行展開闡述。 請感興趣的讀者自行閱讀《Game Theory》\(4.3\)~\(4.4\)，\(5.1\)~\(5.4\) 。

第五部分來自 OI wiki 和 Coco_T

五、樹上刪邊游戲

游戲規則

​ 從某一棵樹上刪除一條邊，同時刪去所有在刪除邊后不再與根相連的部分。雙方輪流進行，無法再進行刪除者判定為失敗，也就是比你拿掉最后一部分你就贏了。一個游戲中有多棵樹，我們把它們的根都掛在天花板上…或者說，放在地板上也行..這么做是為了方便后面的一些解釋和處理。

​ 在這篇文章中，我們討論的將是公平游戲，也就是雙方可以刪除任意的邊，我們稱這個游戲為：Green Hackenbush，暫且稱之為樹上公平刪邊游戲。這個命名是因為還有另外一種刪邊游戲，為不公平的，參與者雙方一方只能刪除藍色邊，一方只能刪除紅色邊，而綠色邊是兩邊都可以刪除的。

竹子竹子！

為了更好地解決樹上刪邊游戲的相關問題，我們引入“竹子”。竹子長的像下面這樣

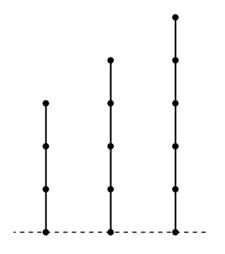
	根據上面的游戲規則，拿掉竹子上的某一節，那么竹子上面的那些也會跟着被刪掉。仔細想想會發現，這不就是最簡單的Nim游戲嗎？有很多堆火柴，每次只能拿走某一堆火柴中的任意數量的火柴。而這里則是有很多個種在地板上的竹子，我們每次只能選一根出來，任意砍掉一部分或者全部。既然發現這是Nim游戲了，那么相應的SG值就知道了: g(x)=x..

克朗原理

	搞定竹子之后，我們就可以來研究樹上刪邊游戲究竟要怎么解決。其實，樹上刪邊游戲就是個披了層樹皮的Nim游戲。為什么這么說呢，我們介紹克朗原理

克朗原理：對於樹上某一個點，它的分支可以轉換為以這個點為根的一根竹子，這個竹子的長度等於它各個分支的邊的數量的異或和。

（怕翻譯不好所以把原文放上來：When branches come together at a vertex, one may replace the branches by a non-branching stalk of length equal to their nim sum.）

現在我們來分析下圖所示的樹上刪邊游戲。

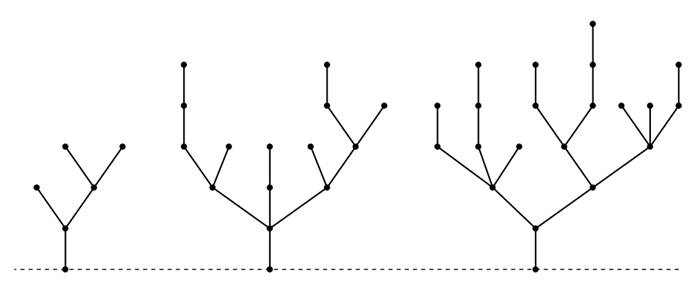
​ 對於第一個圖，1號點有2個分支，分支上的邊樹分別為1、1，異或和為0，所以1號點的分支被替換為長度為0的竹子，也就是說上面兩個分支被刪掉了。所以對於2號點，就剩下2個分支，同理被消掉。最后這個圖被轉化為一根長度為1的竹子，其SG值為1。

	 對於第二個圖，分析過程如下，SG值=8

​ 對於最后一個圖，同理可以得出 \(SG\) 值=4。

​ 現在，我們就可以算出這個游戲在當前狀態的SG值：\(1\) xor \(8\) xor \(4=13 ≠0\)，所以這個是先手必勝狀態，也就是N位置。然后剩下的就是找要到刪去哪條邊了。

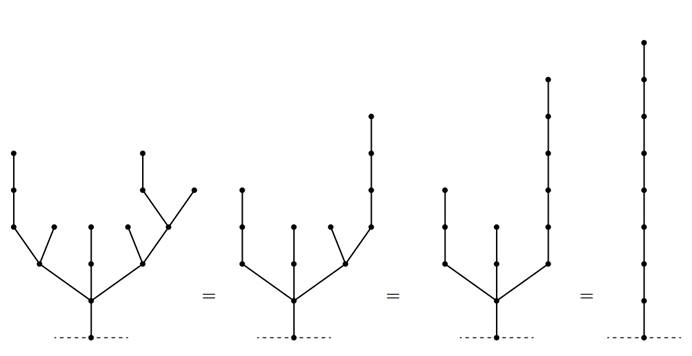
​ 假設我們要刪掉的是圖3.1中第二棵樹上的某一條邊，也就是說，我們要讓這棵樹的SG值變為 1 xor 4=5，才能使得到的游戲狀態的SG值為0.

​ 我們看圖3.2中的倒數第二個圖，這里面所得到的竹子長度： 3 xor 2 xor 6=7，我們要讓它變成4，這樣子加上最下面那條邊的話得出來就是5. 因為 2 xor 6=4，所以可以直接刪掉最左邊的3條邊。當然，如果要刪除中間的話，那么刪除的條數就是 2-4 xor 3 xor 6=1,同理，刪除最右邊的話，就要刪去 6-4 xor 3 xor 2=1條。

​ 好了，這樣子我們就利用克朗原理解決了樹上刪邊游戲的問題。關於克朗原理的證明，因為筆者比較懶所以就不翻譯過來了。請看下面這段：

Proof of the Colon Principle. Consider a fixed but arbitrary graph, G, and select an arbitrary vertex, x, in G. Let H1 and H2 be arbitrary trees (or graphs) that have the same Sprague-Grundy value. Consider the two graphs G1 = Gx : H1 and G2 = Gx : H2, where Gx : Hi represents the graph constructed by attaching the tree Hi to the vertex x of the graph G. The colon principle states that the two graphs G1 and G2 have the same Sprague-Grundy value. Consider the sum of the two games as in Figure 6.4(下圖).

The claim that G1 and G2 have the same Sprague-Grundy value is equivalent to the claim that the sum of the two games has Sprague-Grundy value 0. In other words, we are to show that the sum G1 +G2 is a P-position. (證明兩個游戲的SG值相同，只要證明它們的SG值異或后為0即可，也就是看成一個Nim游戲的和來理解)

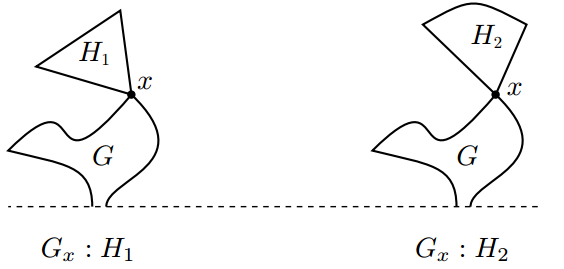
Here is a strategy that guarantees you a win if you are the second player to move in G1 + G2. If the first player moves by chopping one of the edges in G in one of the games, then you chop the same edge in G in the other game. (Such a pair of moves may delete H1 and H2 from the games, but otherwise H1 and H2 are not disturbed.) If the first player moves by chopping an edge in H1 or H2, then the Sprague-Grundy values of H1 and H2 are no longer equal, so that there exists a move in H1 or H2 that keeps the Sprague-Grundy values the same. In this way you will always have a reply to every move the opponent may make. This means you will make the last move and so win.(其實就是輪流取，慢拿的肯定贏，因為每次都可以拿走和被取走那部分SG值相同的。)

​ 其實克朗原理的意思應該這么理解，對樹上一個點，在它的分支都被轉換成竹子之后，我們可以求出它的SG值，而克朗原理是說，可以將它替換稱一個SG值相同的竹子。其實，不單單對於樹上刪邊游戲，應該是對於博弈論大部分問題，只要SG值相同，都可以相互轉換。上面的證明是證明可以轉換的原因。

圖上刪邊游戲

研究過樹上的，現在來討論下圖上刪邊游戲的。就像下面這樣的圖：

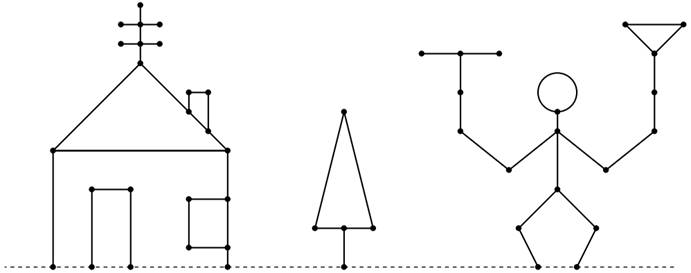
在《Game Theory》的第四章中，我們知道任意一個圖都可以等價為一個Nim游戲中的火柴堆(Nim堆)。為了找到這個火柴堆，我們需要試着把這個圖轉換成一棵樹，然后就可以用上面的辦法轉換成一個Nim堆。這里我們介紹另一個原理，費森原理。

費森原理：環上的點可以在被融合，且不改變圖的 SG 值。

（原文：The vertices on any circuit may be fused without changing the Sprague-Grundy value of the graph.）

其實這個原理看起來好像沒什么用，但是，這個原理使我們能將一個圖去化簡成為我們能夠計算的樣子。現在我們看看在圖4.1是怎么化簡的。

首先，我們先研究下最左邊那個房子的門。如圖4.2所示，地板上的那兩個點可以看成一個，因為地板其實就是一個點，那么門就變成了地板上的一個三角形。接着，就用到費森原理了。三角形是一個環，而我們可以把環上的點換成連在一個點上的三個環。其實這里可以看出，費森原理是允許我們將環上的點換成一個環去表示。最后，每個環分別等價於一個大小為1的Nim堆，所以這三個環的異或和(Nim sum，后稱為Nim和)是1，等價於一個大小為1的 Nim堆。

一般來說，我們可以把一個帶有奇數邊的環等價於只有一個端點的一條邊，而偶數邊的環等價於一個點。舉個例子，圖4.1中第二個圖，樹上的環帶有4條邊，等價於一個點，所以這棵樹就被等價為一條邊，即等價於一個大小為1的Nim堆。同樣的，圖4.1中的房子上的煙囪可以等價為一個點，右邊的窗也可以等價為一個點。接着，如圖4.3進行轉換，我們會得到房子的SG值為3。

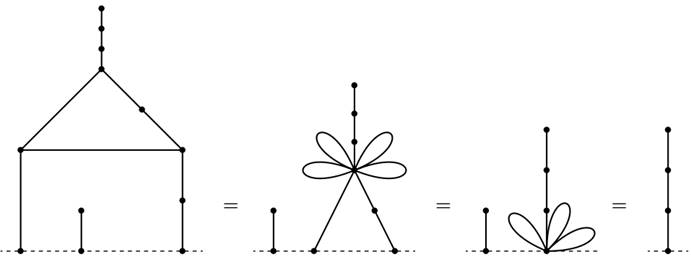
下面，請自己嘗試計算圖4.1最右邊的人的SG值，答案為4。然后，試試看你能不能找到圖4.1為狀態的游戲的解法。

練習

《Game Theory》給的練習真的是太逗了。

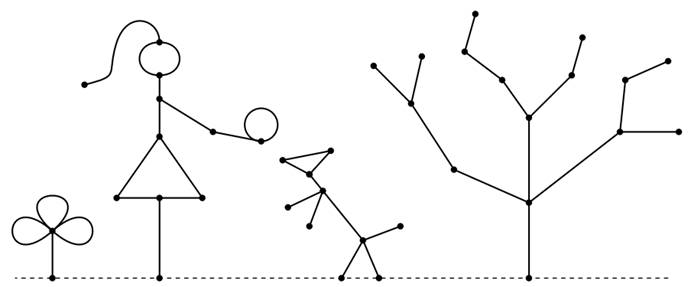
答案（從右到左）: 2 4 2 5