本章是對應用系統負載和磁盤容量進行分析和預測,涉及到的數據為時間序列數據,因此最后是用ARMA模型去擬合。
本文主要包含以下部分:
- ARMA模型
- 平穩性檢驗
- 白噪聲檢驗
- Python實戰
- 總結
ARMA模型
關於ARMA模型,具體可看 [ 時間序列中的ARMA模型
](http://www.morefund.com/a/duichongshidian/2011/0422/327.html) 和 [ ARMA百度百科
](https://baike.baidu.com/item/ARMA模型/8048415?fr=aladdin) 。
本文摘錄其主要部分:
模型基本原理
將預測指標隨時間推移而形成的數據序列看作是一個隨機序列,這組隨機變量所具有的依存關系體現着原始數據在時間上的延續性。一方面,影響因素的影響,另一方面,又有自身變動規律,假定影響因素為
x 1 , x 2 ,…, x k ,由回歸分析,

其中Y是預測對象的觀測值,Z為誤差。作為預測對象Yt受到自身變化的影響,其規律可由下式體現,

誤差項在不同時期具有依存關系,由下式表示,

由此,獲得ARMA模型表達式:

其他的模型定義:

ARIMA模型運用的流程
- 根據時間序列的散點圖、自相關函數和偏自相關函數圖識別其平穩性。
- 對非平穩的時間序列數據進行平穩化處理。直到處理后的自相關函數和偏自相關函數的數值非顯著非零。
- 根據所識別出來的特征建立相應的時間序列模型。平穩化處理后,若偏自相關函數是截尾的,而自相關函數是拖尾的,則建立AR模型;若偏自相關函數是拖尾的,而自相關函數是截尾的,則建立MA模型;若偏自相關函數和自相關函數均是拖尾的,則序列適合ARMA模型。
- 利用已通過檢驗的模型進行預測。
平穩性檢驗
按照上文所述,在進行時間序列模型選擇之前需要對數據平穩性進行檢驗,接下來本文將對平穩性的定義和檢驗方法進行概述,主要內容參考自 [ 時間序列的平穩性及其檢驗
](https://wenku.baidu.com/view/75479e2ff8c75fbfc67db218.html) 。
時間序列的平穩性定義
定義:假定某個時間序列是由某一隨機過程(stochastic process)生成的,如果滿足下列條件:
- 均值E( X t )=μ是與時間t 無關的常數;
- 方差Var( X t )=σ是與時間t 無關的常數;
- 協方差Cov( X t , X t + k )= γ k 是只與時期間隔k有關,與時間t 無關的常數;
則稱該隨機時間序列是 平穩 的(stationary),而該隨機過程是一 平穩隨機過程 (stationary stochastic
process)。
平穩性檢驗的圖示判斷
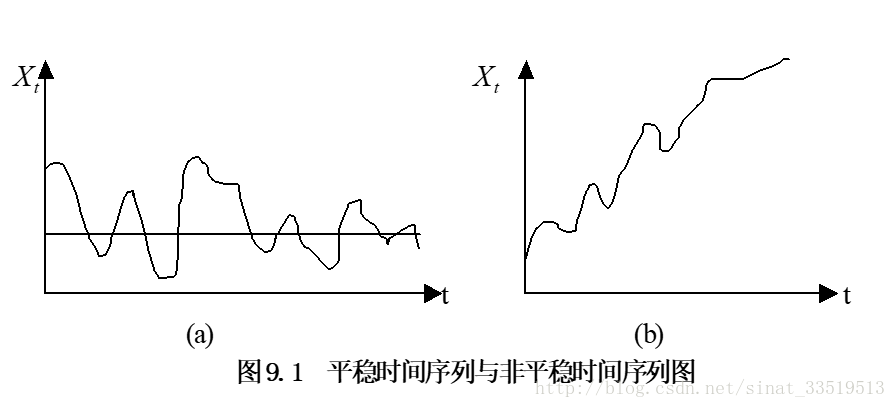
首先,可通過該序列的 時間路徑圖 來粗略地判斷它是否是平穩的。
- 一個 平穩的時間序列 在圖形上往往表現出一種圍繞其均值不斷波動的過程。
- 而 非平穩序列 則往往表現出在不同的時間段具有不同的均值(如持續上升或持續下降)。
具體如圖:
進一步,可通過 檢驗樣本自相關函數及其圖形 來判斷。
定義隨機時間序列的自相關函數(autocorrelation function, ACF)如下:
ρ k = γ k / γ 0
自相關函數是關於滯后期k的遞減函數。
實際上,對一個隨機過程只有一個實現(樣本),因此,只能計算 樣本自相關函數 (Sample autocorrelation function)。
一個時間序列的樣本自相關函數定義為 :

隨着k的增加,樣本自相關函數下降且趨於零。但從下降速度來看,平穩序列要比非平穩序列快得多。
具體如下圖:

根據書上內容,平穩性檢驗較為常用的方法還有 單位根檢驗(ADF)
。單位根檢驗是指檢驗序列中是否存在單位根,如果存在單位根就是非平穩時間序列了。單位根就是指單位根過程,可以證明,序列中存在單位根過程就不平穩,會使回歸分析中存在偽回歸。具體可看
[ 單位根檢驗
](https://baike.baidu.com/item/單位根檢驗/5574482?fr=aladdin)
和 時間序列數據的平穩性檢驗
。
白噪聲檢驗
由書中內容可知,為了驗證序列中有用的信息是否已被提取完畢,需要對序列進行白噪聲檢驗,如果是白噪聲序列,則說明序列中有用的信息已經被提取完畢,剩下的全是隨機擾動,無法進行預測和使用。接下來本文將對白噪聲序列的定義和檢驗方法進行概述。
白噪聲序列定義
白噪聲(對一系列的 ε 1 , ε 2 , ε 3 ….. ε t )定義就三個條件:
- E( ε t )=0
- Var( ε t )= σ 2
- Cov( ε t , ε s )=0 (其中t≠s)
白噪聲檢驗方法
按照書中所說,可以用LB統計量進行檢驗,具體過程如下:
可檢驗對所有k>0,自相關系數都為0的聯合假設,這可通過如下QLB統計量進行:

該統計量近似地服從自由度為m的 χ 2 分布(m為滯后長度)。
因此:如果計算的Q值大於顯著性水平為α的臨界值,則有1-α的把握拒絕所有 ρ k (k>0)同時為0(該序列是白噪聲序列)的假設。
注:上述平穩定檢驗的鏈接里,這一段也在平穩性檢驗里,但通過其他資料的查看,本人認為這一段應該算是在檢驗白噪聲了,其實不管是平穩性檢驗(主要方法是ACF)還是白噪聲檢驗(LB統計量)都是
對時間序列是否存在滯后相關的一種統計檢驗 。
Python實戰
接下來,本文對書中應用系統負載分析與磁盤容量預測的實戰過程做一個記錄。
首先,導入數據,並對數據中C盤和D盤的使用情況做一個 探索性分析 。
代碼如下:
# -*- coding: utf-8 -*-
import pandas as pd
from pandas import Series,DataFrame
import numpy as np
import matplotlib.pyplot as plt
###探索性分析
#設置字體
plt.rcParams['font.sans-serif'] = ['simHei']
plt.rcParams['axes.unicode_minus'] = False
#讀取數據
data=pd.read_excel("D:/ProgramData/PythonDataAnalysiscode/chapter11/demo/data/discdata.xls")
#根據C盤和D盤分列數據
data_C=data[(data['ENTITY']=='C:\\')&(data['DESCRIPTION']==u'磁盤已使用大小')]
data_D=data[(data['ENTITY']=='D:\\')&(data['DESCRIPTION']==u'磁盤已使用大小')]
fig=plt.figure(figsize=(20,20))
ax1=fig.add_subplot(2,1,1)
ax2=fig.add_subplot(2,1,2)
ax1.plot(data_C['VALUE'],'o-')
ax1.set_xlim([0,185])
ax1.set_ylim([33000000,36000000])
ax1.set_title(u'C盤使用情況')
data_C['VALUE'].plot()
ax2.plot(data_D['VALUE'],'o-')
ax2.set_xlim([0,185])
ax2.set_ylim([78000000,92000000])
ax2.set_title(u'D盤使用情況')
plt.show()
結果如下圖:
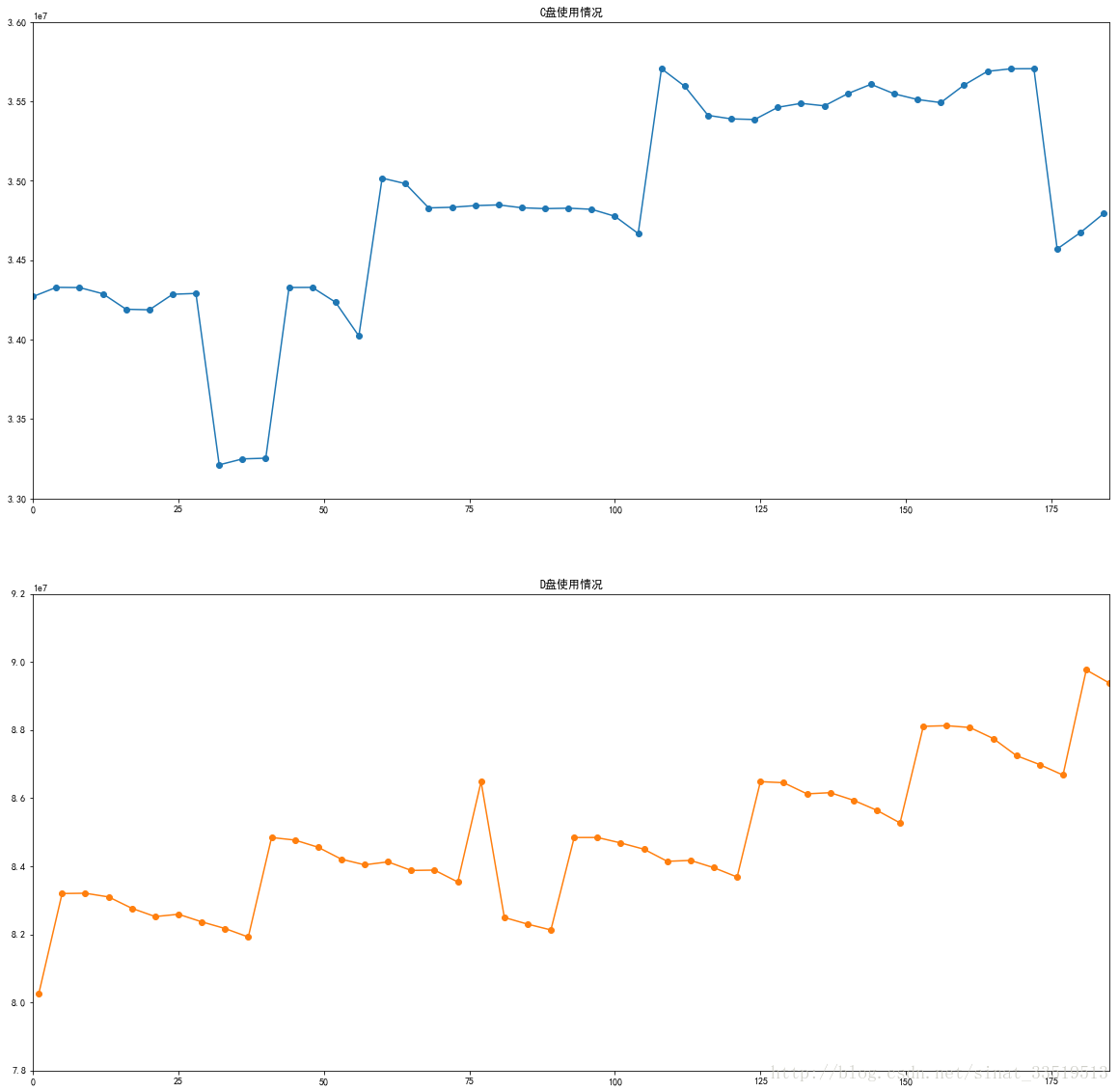
由圖可以看出,不管是C盤還是D盤,其使用情況都不具備周期性,表現出緩慢性地增長,呈現趨勢性。因此,可初步判斷數據是非平穩的。
然后,對 數據進行數據預處理
,主要包括數據清洗和屬性轉換。其中,數據清洗主要是將磁盤容量的重復值刪除,而屬性轉換則是將代表磁盤屬性的三個不變屬性進行合並作為一個新的變量,並將C盤和D盤的數據分成兩個屬性。
代碼如下:
# -*- coding: utf-8 -*-
import pandas as pd
from pandas import Series,DataFrame
import numpy as np
#讀取數據
data=pd.read_excel("D:/ProgramData/PythonDataAnalysiscode/chapter11/demo/data/discdata.xls")
###數據預處理
#數據清洗,刪除重復值(磁盤容量)
data=data.drop_duplicates(['DESCRIPTION','VALUE'])
data_size=data[data['DESCRIPTION']==u'磁盤容量']
#磁盤容量數據行可以不要
data=data[data['DESCRIPTION']!=u'磁盤容量']
data_size.to_excel("D:/ProgramData/PythonDataAnalysiscode/chapter11/demo/data/discdata_orsize.xls")
#屬性構造
data_group=data.groupby('COLLECTTIME')
def attr_trans(x):
result=pd.Series(index=['SYS_NAME','CWXT_DB:184:C:\\','CWXT_DB:184:D:\\','COLLECTTIME'])
result['SYS_NAME']=x['SYS_NAME'].iloc[0]
result['CWXT_DB:184:C:\\']=x['VALUE'].iloc[0]
result['CWXT_DB:184:D:\\']=x['VALUE'].iloc[1]
result['COLLECTTIME']=x['COLLECTTIME'].iloc[0]
return result
data_processed=data_group.apply(attr_trans)
[/code]
最后得到的部分數據結果如下:
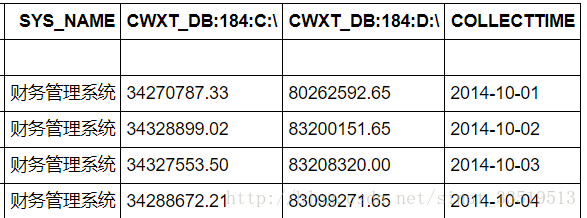
最后,進行模型構建。如上文所說,模型構建之前需要先對數據進行平穩性檢驗和白噪聲檢驗。
**利用單位根檢驗(ADF)進行平穩性檢驗** 和平穩化處理的代碼如下:
```code
import pandas as pd
#讀取數據
#必須要加index_col,否則后面模型識別時會因為沒有時間數據而出錯
df=pd.read_excel("D:/ProgramData/PythonDataAnalysiscode/chapter11/demo/data/discdata_processed.xls",index_col='COLLECTTIME')
#用單位根檢驗(ADF)進行平穩性檢驗
data=df.iloc[:(len(df)-5)]
from statsmodels.tsa.stattools import adfuller as ADF
diff=0
adf=ADF(data['CWXT_DB:184:D:\\'])
if adf[1]>0.05:
print (u'原始序列經檢驗不平穩,p值為:%s'%(adf[1]))
else:
print (u'原始序列經檢驗平穩,p值為:%s'%(adf[1]))
while adf[1]>=0.05:#adf[1]為p值,p值小於0.05認為是平穩的
diff=diff+1
adf=ADF(data['CWXT_DB:184:D:\\'].diff(diff).dropna())
print (u'原始序列經過%s階差分后歸於平穩,p值為%s'%(diff,adf[1]))
[/code]
輸出結果為:
【原始序列經檢驗不平穩,p值為:0.0838488963412
原始序列經過1階差分后歸於平穩,p值為4.79259126339e-07】
**采用LB統計量的方法進行白噪聲檢驗** 的代碼如下:
```code
#采用LB統計量的方法進行白噪聲檢驗
from statsmodels.stats.diagnostic import acorr_ljungbox
[[lb],[p]]=acorr_ljungbox(data['CWXT_DB:184:D:\\'],lags=1)
if p<0.05:
print (u'原始序列為非白噪聲序列,p值為:%s'%p)
else:
print (u'原始序列為白噪聲序列,p值為:%s'%p)
[[lb],[p]]=acorr_ljungbox(data['CWXT_DB:184:D:\\'].diff().dropna(),lags=1)
if p<0.05:
print (u'一階差分序列為非白噪聲序列,p值為:%s'%p)
else:
print (u'一階差分序列為白噪聲序列,p值為:%s'%p)
[/code]
輸出結果為:
【原始序列為非白噪聲序列,p值為:9.95850372977e-06
一階差分序列為白噪聲序列,p值為:0.114330259776】
最后 **ARMA模型構建** 的代碼如下:
```code
#模型識別
#確定最佳p,d,q值
xdata=data['CWXT_DB:184:D:\\']
from statsmodels.tsa.arima_model import ARIMA
#定階
pmax = int(len(xdata)/10) #一般階數不超過length/10
qmax = int(len(xdata)/10) #一般階數不超過length/10
bic_matrix = [] #bic矩陣
for p in range(pmax+1):
tmp = []
for q in range(qmax+1):
try: #存在部分報錯,所以用try來跳過報錯。
tmp.append(ARIMA(xdata, (p,1,q)).fit().bic)
except:
tmp.append(None)
bic_matrix.append(tmp)
bic_matrix = pd.DataFrame(bic_matrix) #從中可以找出最小值
p,q = bic_matrix.stack().astype('float64').idxmin() #先用stack展平,然后用idxmin找出最小值位置。
print (u'BIC最小的p值和q值為:%s、%s' %(p,q))
輸出結果為:
【BIC最小的p值和q值為:1、1】
模型確立后,還需檢驗其 殘差序列是否為白噪聲 ,如果不是白噪聲,說明殘差中還存在有用的信息,需要修改模型或進一步提取。
檢驗代碼如下:
#模型檢驗:模型確立后,檢驗其殘差序列是否為白噪聲
lagnum=12#殘差延遲個數
from statsmodels.tsa.arima_model import ARIMA #建立ARIMA(p,1,q)模型
arima = ARIMA(xdata, (p, 1, q)).fit() #建立並訓練模型
xdata_pred = arima.predict(typ = 'levels') #預測
pred_error = (xdata_pred - xdata).dropna() #計算殘差
from statsmodels.stats.diagnostic import acorr_ljungbox #白噪聲檢驗
lb, p_l= acorr_ljungbox(pred_error, lags = lagnum)
h = (p_l < 0.05).sum() #p值小於0.05,認為是非白噪聲。
if h > 0:
print (u'模型ARIMA(%s,1,%s)不符合白噪聲檢驗'%(p,q))
else:
print (u'模型ARIMA(%s,1,%s)符合白噪聲檢驗' %(p,q))
輸出結果為:
【模型ARIMA(1,1,1)符合白噪聲檢驗】。
通過檢驗之后,進行 預測 。
#模型預測
test_predict=arima.forecast(5)[0]
print (test_predict)
#預測對比
test_data=pd.DataFrame(columns=[u'實際容量',u'預測容量'])
test_data[u'實際容量']=df[(len(df)-5):]['CWXT_DB:184:D:\\']
test_data[u'預測容量']=test_predict
[/code]
最后的結果為:
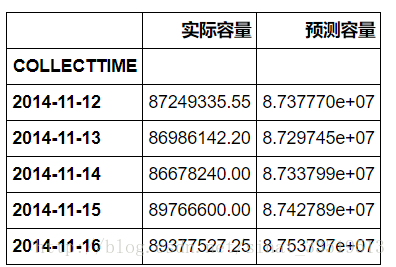
誤差絕對值為:
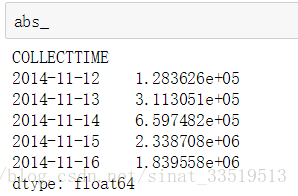
出來的差距有點大,與書上不符,且上文中最后的模型是ARIMA(1,1,1),也與書上的ARIMA(0,1,1)不一樣,不知是哪里出了問題。
## 總結
第十章學習到此結束,雖然最后結果不太一樣,但這個過程中對時間序列模型、平穩性檢驗、白噪聲檢驗等都有了一定了解,還是獲益匪淺。

